1. 拓扑排序

（1）定义

AOV网：顶点表示活动，有向边 $V_i,V_j>$ 表示活动 $V_i$ 先于活动 $V_j$ 进行的一种关系。
①AOV网一定是有向无环图。
②任何顶点不能以自己作为其前驱或后继。
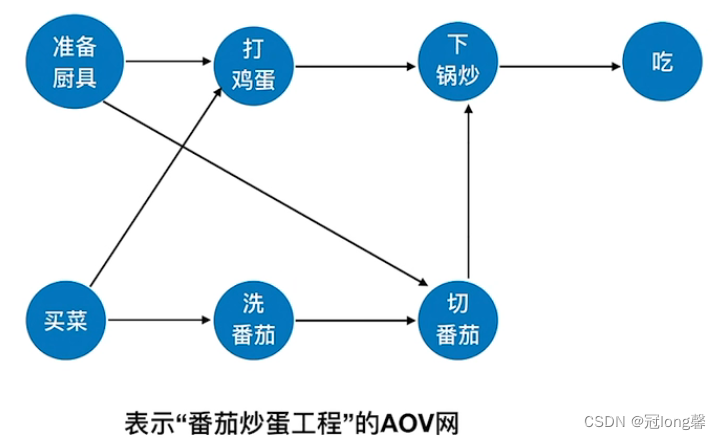
拓扑排序：对有向无环图顶点的一种排序。使得若存在一条从顶点A到顶点B的路径，则在排序中顶点B出现在顶点A的后面。
①理解为工程事件执行的先后次序。
②一个AOV网可能有多种拓扑排序。

（2）思路
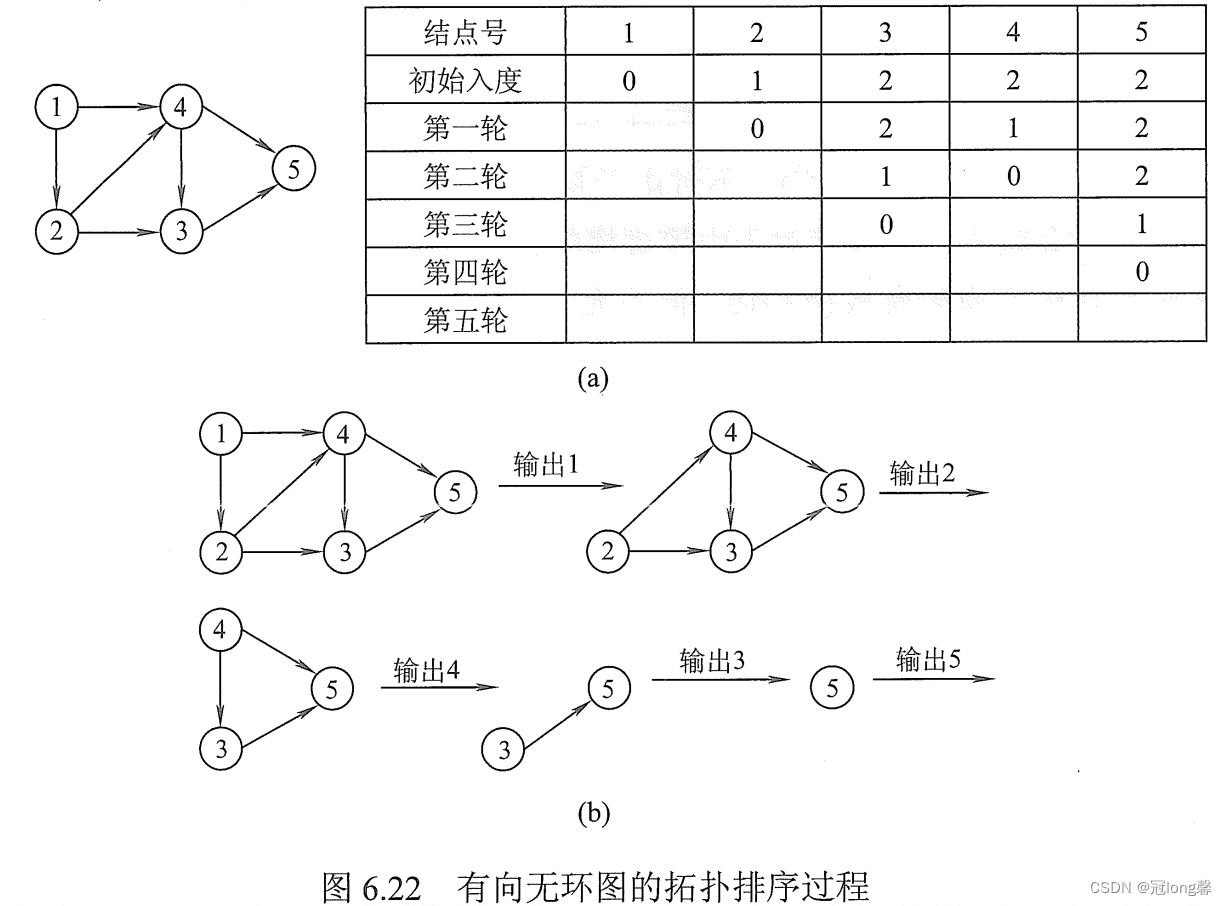
初始化时将AOV网中所有入度为0的顶点加入栈中。

从栈中选择一个入度为0的顶点并输出。
删除该顶点和以它为起点的有向边。
循环步骤1、2，直到AOV网为空或当前网中不存在无前缀的顶点。

/*
indegree[vexnum]：顶点的入度向量
s：栈
*/
bool ToplogicalSort(Gragh G) {
	// 1. 初始化栈
	for(int i=0; i<G.vexnum; i++)
		if(indegree[i] == 0)
			S.push(i);
	int count = 0;	
	// 2. 循环取出入度为0的顶点并删除其输出边
	while(!S.empty()) {
		i = S.top();	S.pop();
		count++;
		for(p=G.vertices[i].firstarc;p;p=p->nextarc)	// 邻接顶点
		{
			v = p->adjvex;	// 序号
			if((--indegree[v]) == 0)
				S.push(v); 
		}
	}
	// 3. 判断排序是否成功
	if(count < G.vexnum)
		return false;
	else return true;
}

（3）时间复杂度

采用邻接表存储图时，时间复杂度为 $O (∣ V ∣ + ∣ E ∣)$ 。
采用邻接矩阵存储图时，时间复杂度为 $O(|V|^2)$ 。

2. 逆拓扑排序

（1）思路
初始化时将AOV网中所有出度为0的顶点加入栈中。

从栈中选择一个出度为0的顶点并输出。
删除该顶点和以它为终点的有向边。
循环步骤1、2，直到AOV网为空或当前网中不存在无前缀的顶点。

3. 关键路径

（1）定义

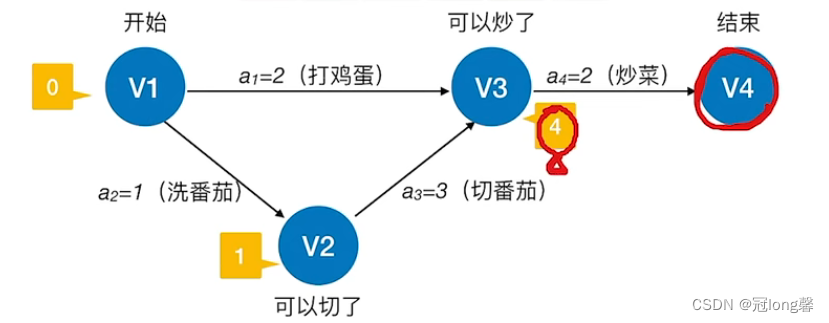
AOE网：在带权有向图中，以顶点表示事件，以有向边表示活动，以边上的权值表示完成该活动的开销。
①AOE网中边有权值，AOV网中边无权值。
②只有在某个顶点代表的事件发生后，从该顶点出发的各有向边所代表的活动才能开始。
③只有在进入某顶点的所有边代表的活动都结束时，该顶点所代表的事件才能发生。
开始顶点：仅有的一个入度为0的顶点，称为源点。
结束顶点：仅有一个出度为0的顶点，称为汇点。
关键路径：从源点到汇点的所有路径中，具有最大路径长度的路径。
①关键路径表示完成整个工程需要的最短时间
关键活动：关键路径上的活动。
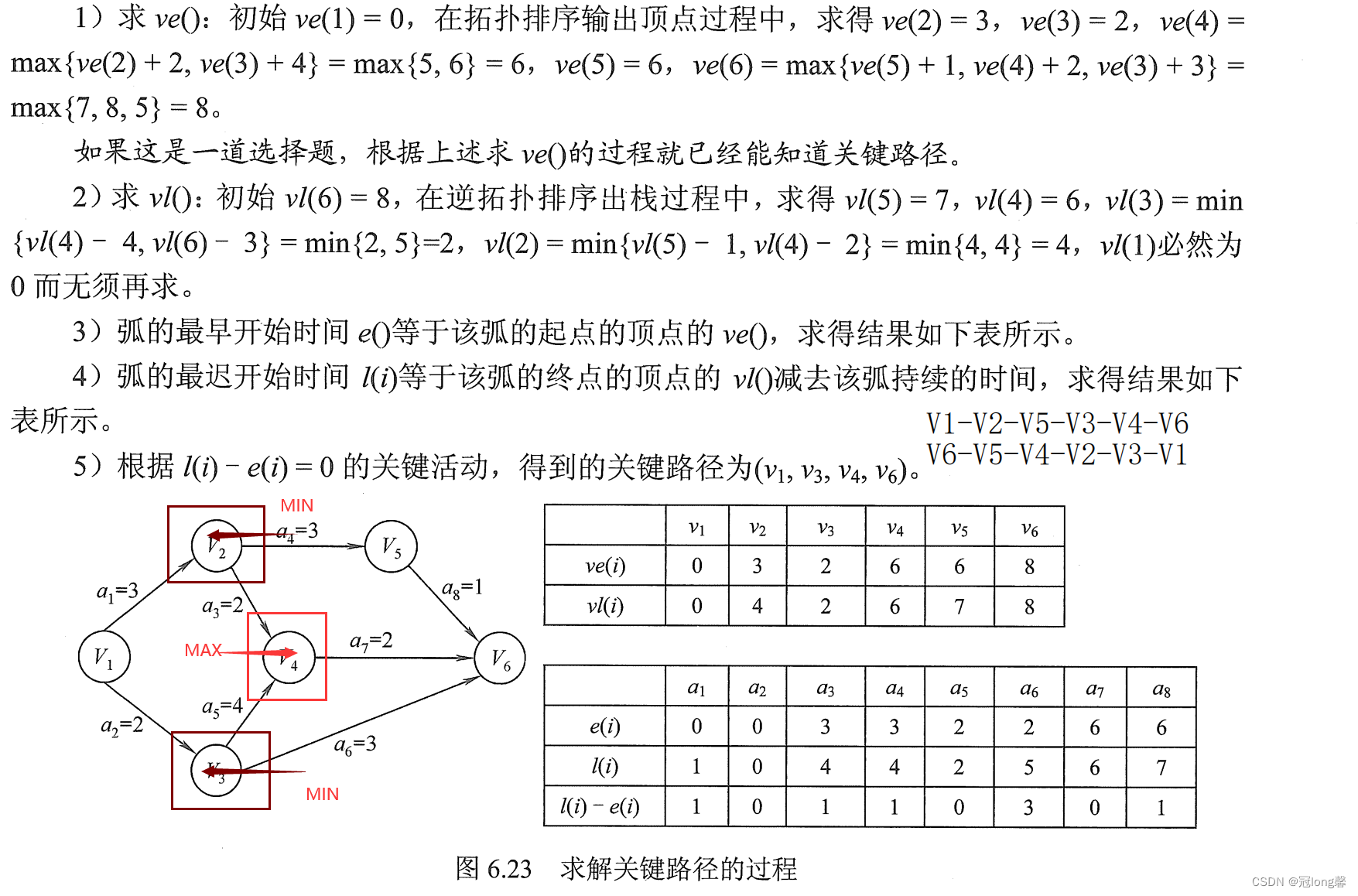
事件 $v_k$ 的最早发生时间ve：指从源点到顶点的最长路径长度。
活动的最早发生时间e：弧的起点表示的事件的最早发生时间ve。
事件的最迟发生时间vl：
活动的最迟发生时间l：弧的起点表示的事件的最迟发生时间vl。
活动的时间余量：等于活动最迟开始时间-活动最早开始时间。