T树

键树又称数字查找树（Digital Search Trees），它是一颗度>=2的树，树种的每个结点中不是包含一个或几个关键字，而是只含有组成关键字的符号，例如，若关键字是数值，则结点中只包含一个数位；若关键字是单词，则结点中只包含一个字母字符，这种树会给某种类型关键字的表的查找带来方便
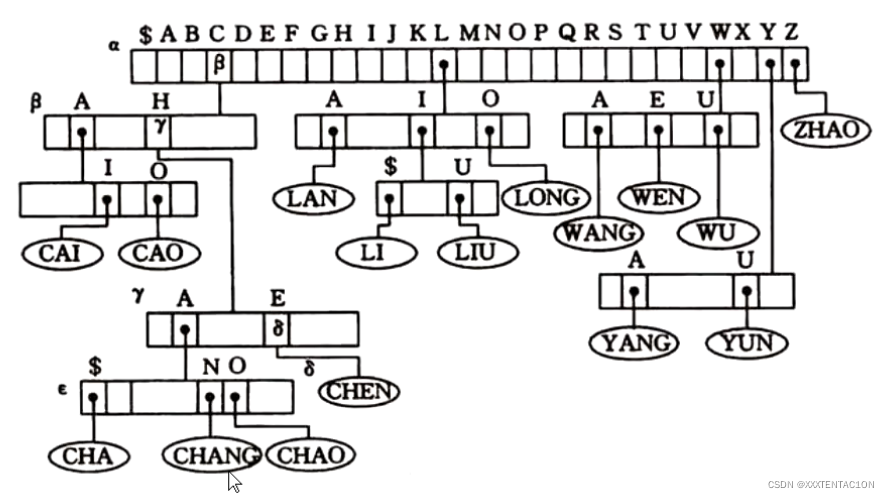
在这里插入图片描述

T树的定义

const int MaxKeySize = 25;
const int LETLEN = 27;
typedef enum { BRCH = 0, ELEM = 1 } NodeType;

struct TrieNode;
typedef struct
{
	char ch[MaxKeySize];
	int curentSize;
}KeyType;
typedef struct  //元素 
{ 
	KeyType key;
	void* recptr;
}ElemType;   //key_value

typedef struct  //分支
{
	TrieNode* link[LETLEN];

}BrchType;

struct TrieNode
{
	NodeType type;
	union
	{
		ElemType item;
		BrchType brch;
	};
}

T树的插入

T树的插入就像再电话簿里插入电话一样，首先去找分支若没有分支则创建一个分支，再进行元素的插入，并且由于T树的特殊性，不能对T树进行删除操作

const int MaxKeySize = 25;
const int LETLEN = 27;
typedef enum { BRCH = 0, ELEM = 1 } NodeType;

struct TrieNode;
typedef struct
{
	char ch[MaxKeySize];
	int curentSize;
}KeyType;
typedef struct  //元素 
{ 
	KeyType key;
	void* recptr;
}ElemType;   //key_value

typedef struct  //分支
{
	TrieNode* link[LETLEN];

}BrchType;

struct TrieNode
{
	NodeType utype;
	union
	{
		ElemType item;  //元素
		BrchType brch;  //分支
	};
};

class TrieTree
{
private:
	TrieNode* root;
	static TrieNode* Buynode()
	{
		TrieNode* s = (TrieNode*)malloc(sizeof(TrieNode));
		if (nullptr == s)exit(1);
		memset(s, 0, sizeof(TrieNode));
		return s;
	}

	static int Index(const KeyType& kx, int k)
	{
		int index = 0;
		if (k < kx.curentSize)
		{
			index = kx.ch[k] - 'a' + 1;
		}
		return index;
	}

	static TrieNode* MakeElem(const ElemType& item) 
	{
		TrieNode* s = Buynode();
		s->utype = ELEM;
		s->item = item;
		return s;
	}
	static TrieNode* MakeBrch(TrieNode* ptr, int k)
	{
		TrieNode* s = Buynode();
		s->utype = BRCH;
		int index = Index(ptr->item.key, k);

		s->brch.link[index] = ptr;
		return s;
	}


public:
	TrieTree() :root(nullptr) {}
	~TrieTree() {}

	TrieNode* Find(const KeyType& kx)
	{
		TrieNode* p = root;
		int k = 0;
		while (p != nullptr && p->utype == BRCH)//分支
		{
			int index = Index(kx, k);
			k += 1;
			p = p->brch.link[index];
		}
		if (p != nullptr && strcmp(kx.ch, p->item.key.ch) != 0) //没找到 
		{
			p = nullptr;
		}
		return p;
	}

	void Insert_Item(TrieNode*& ptr, const ElemType& item, int k)
	{
		if (ptr == nullptr) //根为空
		{
			ptr == MakeElem(item); //建立元素结点
		}
		else if (ptr->utype == BRCH)
		{
			int index = Index(item.key, k);
			Insert_Item(ptr->brch.link[index], item, k + 1);
		}
		else if (ptr->utype == ELEM)
		{
			ptr = MakeBrch(ptr, k); //建立分支
			int index = Index(item.key, k);
			Insert_Item(ptr->brch.link[index], item, k + 1);
		}
	}
	bool Insert(const ElemType& item)
	{
		TrieNode* p = Find(item.key); //防止重赋值
		if (p != nullptr) 
		{
			return false;
		}
		int k = 0;
		Insert_Item(root, item, k);

		return true;
	}

};

int main()
{
	TrieTree tt;
	KeyType kx[] = { "data",4,"eye",3 ,"date",4,"dat",3,"egg",3};
	int n = sizeof(kx) / sizeof(kx[0]);
	for (int i = 0; i < n; ++i)
	{
		ElemType item = { kx[i],nullptr };
		tt.Insert(item);
	}

	return 0;
}