目录
做题链接
35. 搜索插入位置 - 力扣(LeetCode) (leetcode-cn.com)
题目要求
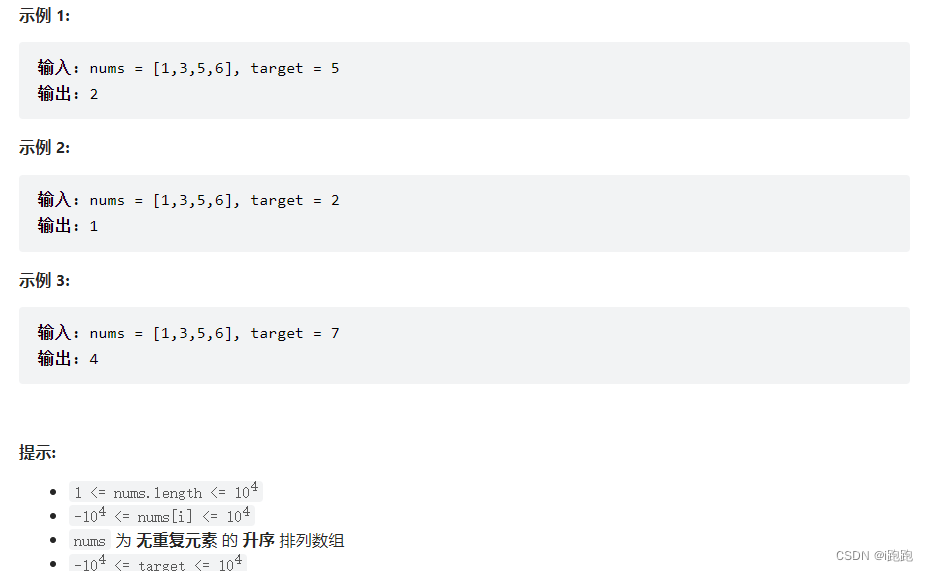
题目示例
思路
关于数组的题目
看到时间复杂度必须使用O(log n),就想到了二分查找
要确定左右下标
还要有中间下标,更新左右下标
还要确定边界情况
边界情况
?
当给定的值最小或等于第一个值时,插入位置在?下标0?处
当给定值最大时,插入位置在下标?numsSize?处
当给定值等于数组最大值时,返回位置下标在?numsSize-1?处
注意:给的是有序数组,边界情况开始直接比较最左边和最右边
int left=0; int right=numsSize-1; if(nums[right] < target) return numsSize; if(nums[right] == target) return right; if(nums[left] >= target) return left;不在边界时
不在边界时,使用二分查找,应有循环,循环条件应该是:
给定值大于最小值,小于最大值
nums[left]<target && nums[right]>target用上述条件进行while循环
在循环中,需要更新左右下标位置,实现时间复杂度O(log n)
给定变量mid,中间下标 mid = (left+right)/2
更新下标
当中间下标位置的值大于给定值
那么插入位置应该在mid左边,更新右下标,right=mid
当中间下标位置的值小于给定值
那么插入位置应该在mid右边,更新左下标,left=mid
当中间下标位置的值等于给定值
那么直接返回下标位置 mid
while(nums[left]<target && nums[right]>target) { int mid=(left+right)/2; if(nums[mid]>target) { right=mid; } if(nums[mid]<target) { left=mid; } if(nums[mid]==target) { return mid; } }解决死循环问题
如果上述循环仅此的话,必然存在死循环问题,以下图为例:
我们不难发现,死循环往往发生在两个相邻下标上
并且当下标相邻后,若会死循环,那么他们第二次循环时
mid是等于left的,因此,我们直接加上left==mid的条件
如果符合:返回right下标即可
改正循环代码
while(nums[left]<target && nums[right]>target) { int mid=(left+right)/2; //防止死循环 if(mid==left) { return right; } if(nums[mid]>target) { right=mid; } if(nums[mid]<target) { left=mid; } if(nums[mid]==target) { return mid; } }确定返回值
当上述循环停下时,必定是其中一个条件不满足上述循环
在此要判断是哪一个不满足循环条件
如果左边满足条件,右边不满足条件:
右边必然是上一步的mid更新来的
只能是小于给定值,不可能等于
直接返回右下标即可,右下标即插入位置
如果右边满足条件,左边不满足条件:
左边必然是上一步的mid更新来的
只能是大于给定值,不可能等于
直接返回左下标即可,左下标即插入位置
if(nums[left]<target) { return right; } if(nums[right]>target) { return left; }
不要忘记最后的返回,见代码最后注释?
完整代码如下:
int searchInsert(int* nums, int numsSize, int target){
int left=0;
int right=numsSize-1;
if(nums[right] < target)
return numsSize;
if(nums[right] == target)
return right;
if(nums[left] >= target)
return left;
while(nums[left]<target && nums[right]>target)
{
int mid=(left+right)/2;
if(mid==left)
{
return right;
}
if(nums[mid]>target)
{
right=mid;
}
if(nums[mid]<target)
{
left=mid;
}
if(nums[mid]==target)
{
return mid;
}
}
if(nums[left]<target)
{
return right;
}
if(nums[right]>target)
{
return left;
}
//最后不要忘记返回噢
return ;
}?


