打家劫舍I
分两种情况
class Solution {
public:
int rob(vector<int>& a) {
int n = a.size();
auto dp = vector<int>(n+1,0);
dp[1]=a[0];
for(int i=2;i<=n;++i){
dp[i] = std::max<int>( a[i-1] + dp[i-2],dp[i-1] );
}
return dp[n];
}
};
dp开三个大小的就够了
class Solution {
public:
int rob(vector<int>& a) {
int n = a.size();
auto dp = vector<int>(3,0);
dp[1]=a[0];
for(int i=2;i<=n;++i){
dp[i%3] = std::max<int>( a[i-1] + dp[(i+1)%3],dp[(i+2)%3] );
}
return dp[n%3];
}
};

打家劫舍III
使用满二叉树的下标方式访问,超时了
第一版想法简单,使用满二叉树
用i*2和i*2+1访问左节点和右节点
dp[i]表示下标为i的子树能取得的最大值
注意更新顺序是从下到上
-----
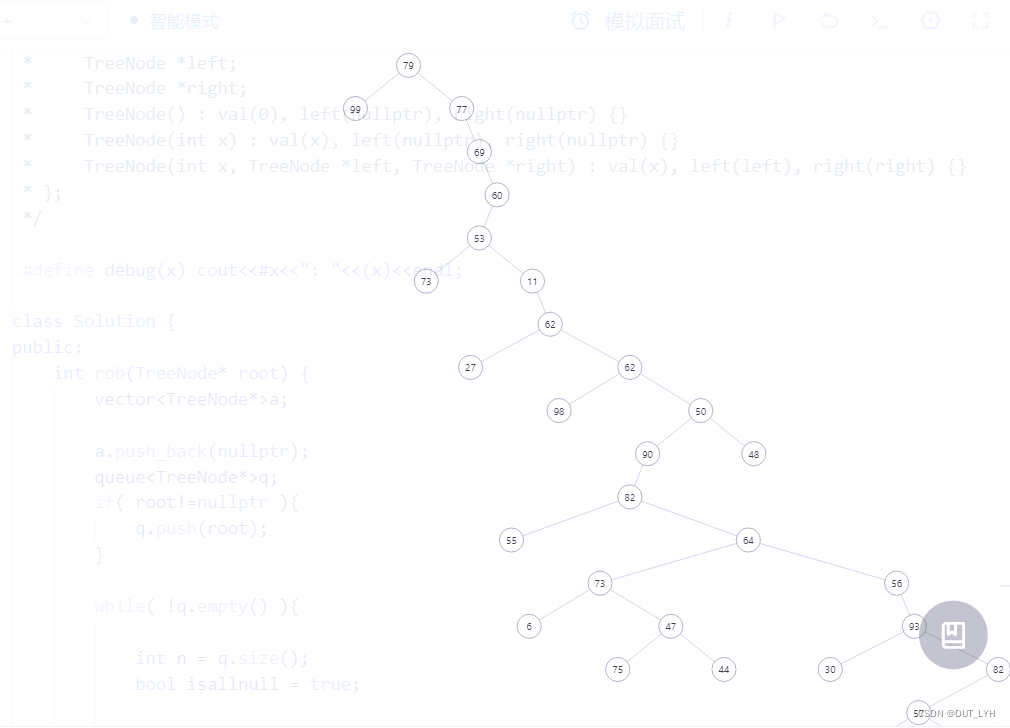
但是因为把空节点也弄进去了,所以如果输入不友好的时候
就像下面的 一个树 居然像个链表,那这复杂度就受不了了
所以不能存空节点
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
#define debug(x) cout<<#x<<": "<<(x)<<endl;
class Solution {
public:
int rob(TreeNode* root) {
vector<TreeNode*>a = {nullptr};
queue<TreeNode*>q;
if( root!=nullptr ){
q.push(root);
}
while( !q.empty() ){
int n = q.size();
bool isallnull = true;
for(int i=0;i<n;++i){
auto fr = q.front();
q.pop();
a.push_back(fr);
if( fr!=nullptr ){
isallnull = false;
q.push(fr->left);
q.push(fr->right);
}else{
q.push(nullptr);
q.push(nullptr);
}
}
if(isallnull){
break;
}
}
int len = a.size();
vector<int> dp(len,0);
vector<bool> isin(len,false);
len/=2;
// debug(len)
for(int i=len-1;i>=1;--i){
if(a[i]!=nullptr){
int l = i*2;
int r = i*2+1;
int chi = 0;
int ll = l*2 >=len?0:dp[l*2];
int lr = l*2+1 >=len?0:dp[l*2+1];
int rl = r*2 >=len?0:dp[r*2];
int rr = r*2+1 >=len?0:dp[r*2+1];
// debug(l)
// debug(r)
dp[i] = std::max<int>(dp[l]+dp[r], ll + lr + rl + rr + a[i]->val);
}else{
dp[i] = 0;
}
}
return dp[1];
}
};
不存空节点
所以dp数组不能用下标访问了,改成了一个hash_map
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
#define debug(x) cout<<#x<<": "<<(x)<<endl;
class Solution {
public:
int rob(TreeNode* root) {
vector<TreeNode*>a;
a.push_back(nullptr);
queue<TreeNode*>q;
if( root!=nullptr ){
q.push(root);
}
while( !q.empty() ){
int n = q.size();
bool isallnull = true;
vector<TreeNode*> t;
for(int i=0;i<n;++i){
// cout<<n<<" ";debug(i)
auto fr = q.front();
q.pop();
a.push_back(fr);
if( fr!=nullptr ){
isallnull = false;
q.push(fr->left);
q.push(fr->right);
}
}
}
int len = a.size();
// debug(len)
unordered_map<TreeNode*,int> dp;
vector<bool> isin(len,false);
for(int i=len-1;i>=1;--i){
if(a[i]!=nullptr){
auto l = a[i]->left;
auto r = a[i]->right;
int ll = l==nullptr || l->left==nullptr ?0:dp[l->left];
int lr = l==nullptr || l->right == nullptr ?0:dp[l->right];
int rl = r==nullptr || r->left == nullptr ?0:dp[r->left];
int rr = r==nullptr || r->right == nullptr?0:dp[r->right];
dp[ a[i] ] = std::max<int>(dp[l]+dp[r], ll + lr + rl + rr + a[i]->val);
}
}
return dp[ a[1] ];
}
};

也可以写成递归的
#define debug(x) cout<<#x<<": "<<(x)<<endl;
class Solution {
public:
vector<int> dfs(TreeNode* rt){
if( rt==nullptr){
return {0,0};
}
//{包含rt,不包含rt }
auto l = dfs(rt->left);
auto r = dfs(rt->right);
//cout<<"rt val:"<<rt->val<<": "<<l[1] + r[1] + rt->val<<", "<<l[0]+r[0]<<endl;
int t = std::max<int>( l[0]+r[0],l[1]+r[1]);
t = std::max<int>( t,l[0]+r[1]);
t = std::max<int>( t,l[1]+r[0]);
return { l[1] + r[1] + rt->val, t };
}
int rob(TreeNode* root) {
auto ret = dfs(root);
return std::max<int>(ret[0],ret[1]);
}
};

