一、TSP简介
旅行商 (TSP) 问题是数学领域组合优化中著名的 NP 难题之一, 又称旅行推销员问题. 该问题的求解一直是学术界研究的热点问题. 旅行商问题的表述比较容易, 但对于路径的优化求解比较困难. 对于 TSP 问题求解的传统方法有蛮力法、动态规划法、分枝限界法等, 但当 TSP 问题的规模较大时, 传统算法往往不能解决. 针对大规模的 TSP 问题, 近年来兴起的群体智能优化算法在该问题的求解中得到了很好的应用。
1 麻雀搜索算法
麻雀搜索算法是受麻雀群体的捕食与反捕食行为启发得来. 麻雀的觅食过程遵循发现者-跟随者模型,同时引入麻雀对于捕食者的预警机制. 麻雀群体种有发现者、跟随者、预警者 3 种角色. 种群中适度值较高的麻雀作为发现者, 负责找到食物并且为其他麻雀提供食物的方位. 除去作为发现者的麻雀, 其他个体则为跟随者, 跟随发现者进行觅食. 同时, 跟随者会监视发现者, 并对其进行食物的掠夺提高自己的适应度, 从而成为发现者. 在麻雀群体中, 存在一定数量的预警者,当预警值大于安全值时, 预警者会发出叫声为其他麻雀提供信号, 逃离危险区域, 防止被捕食. 麻雀搜索算法中麻雀角色具体位置更新公式如下:麻雀种群中的发现者的位置更新公式为:
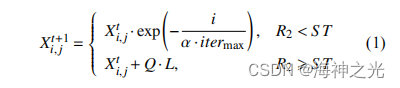
其中, 麻雀种群中发现者所占的比例为 10%–20%, 式 中 t 为当前的迭代数, 为最大迭代数, 为 之间均匀的随机数, , 分别表示预
警值与安全值. Q 为服从正态分布的随机数, L 为的矩阵, 其中每个内部元素都为 1.
麻雀种群中跟随者的位置更新公式为:

其中, 预警者所占的比例为 10%–20%, 为当前麻雀种群的全局最优位置的个体, 为服从正态分布, 均值为 0, 方差为 1 的控制步长的参数, 为一个极小的常数, 用于避免式中分母出现 0 的情况, 一般设为 10E–8.用来控制麻雀的运动方向. 为当前个体 i 的
适应度值, fg, fw为当前麻雀种群的局部最优适度值与最差适度值.
麻雀搜索算法的基本算法步骤如下: 步骤 1. 初始化最大迭代次数, 种群数量 N, 发现这比例 PD, 侦察者比例 SD、警戒阈值 R2. 步骤 2. 计算麻雀种群的适度值并进行排序, 找出当前最差适度个体与最优适度值个体.
步骤 3. 应用式 (1) 对发现者进行位置更新.
步骤 4. 应用式 (2) 对跟随者进行位置更新.
步骤 5. 应用式 (3) 对预警者进行位置更新.
步骤 6. 完成当前迭代, 得到新的位置.
步骤 7. 计算当前麻雀种群的适度值, 如果优于之前位置, 更新麻雀种群位置.
步骤 8. 判断是否满足最大迭代次数或者精度要求, 若是, 结束迭代输出最优结果, 否则返回步骤 3.
二、部分源代码
clc;
三、运行结果


四、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例(第2版)[M].电子工业出版社,2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社,2017.
[3]张月栋,莫愿斌.改进的麻雀搜索算法及其求解旅行商问题[J].计算机系统应用. 2022,31(02)
