问题1:输入一棵二元查找树,将该二元查找树转换成一个排序的双向链表。要求不能创建任何新的结点,只调整指针的指向。
比如:
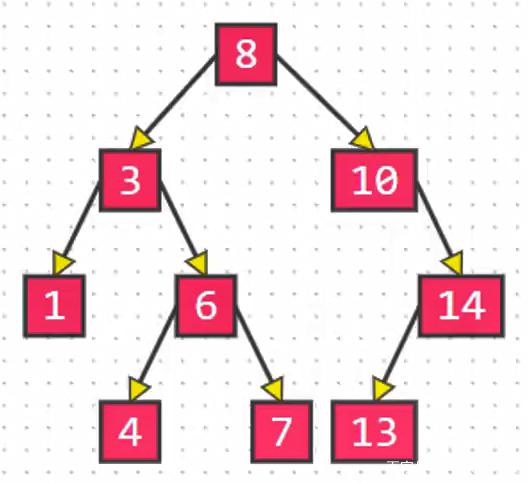
转换成双向链表的顺序是:
1? 3? 4? 6? 7? 8? 10? 13? 14?
步骤一:建立二叉搜索树
struct BSTreeNode
{
int value;
BSTreeNode *left;
BSTreeNode *right;
};
BSTreeNode * Insert(BSTreeNode *p, int x)
{
if(p == NULL)
{
//最终新加的元素将会被赶到最下面,新建这个节点;这么做是遵循二元查找树定义的
//前面也可插入只是太麻烦
p = new BSTreeNode;
p->value = x;
p->left = NULL;
p->right = NULL;
}
else
{
//如果x小于头结点,加到左边
if(p->value > x)
p->left = Insert(p->left, x);
//如果x大于头结点,加到右边
if(p->value < x)
p->right = Insert(p->right, x);
}
return p;
} 步骤二:遍历二元查找树
void Traverse(BSTreeNode *p) //中序遍历
{
if(p == NULL)
return;
Traverse(p->left); //左
cout<<p->value<<' '; //根
Traverse(p->right); //右
} 步骤三:转换为双向链表(比我小之中取最大,比我大之中取最小,分列我两侧)
BSTreeNode * Convert(BSTreeNode *node)
{
if(node == NULL)
return NULL;
BSTreeNode *leftMax,*rightMin;
leftMax = node->left;
rightMin = node->right;
//找到左子树的最大结点
while(leftMax != NULL && leftMax->right != NULL)
leftMax = leftMax->right;
//找到右子树的最小结点
while(rightMin != NULL && rightMin->left != NULL)
rightMin = rightMin->left;
//递归求解 在调整指针之前,先递归
Convert(node->right);
Convert(node->left);
//将左右子树同根结点连起来,只不过是以兄弟的关系
if(leftMax != NULL)
leftMax->right = node;
if(rightMin != NULL)
rightMin->left = node;
node->left = leftMax;
node->right = rightMin;
return node;
} 问题2:输入一颗二元查找树,将该树转换为它的镜像,即在转换后的二元查找树中,左子树的结点都大于右子树的结点。用递归和循环两种方法完成树的镜像转换
struct BSTreeNode
{
int value;
BSTreeNode *left;
BSTreeNode *right;
}; 解法一:用递归
//函数功能 : 输入一颗二元查找树,将该树转换为它的镜像
//函数参数 : pRoot为根结点
//返回值 : 根结点
BSTreeNode * Mirror_Solution1(BSTreeNode * pRoot)
{
if(pRoot != NULL)
{
//必须记住这个节点,不然下面的赋值将把原来的关系解除,就找不到原来的pRoot->left;了
BSTreeNode * pRight = pRoot->right;
BSTreeNode * pLeft = pRoot->left;
pRoot->left = Mirror_Solution1(pRight); //转化右子树
pRoot->right = Mirror_Solution1(pLeft); //转化左子树
}
return pRoot;
} 解法二:用循环
BSTreeNode * Mirror_Solution2(BSTreeNode * pRoot)
{
if(pRoot != NULL)
{
stack<BSTreeNode *> stk; //辅助栈
stk.push(pRoot); //压入根结点
while(stk.size())
{
BSTreeNode *pNode = stk.top();
BSTreeNode *pLeft = pNode->left;
BSTreeNode* pRight = pNode->right;
stk.pop();
if(pLeft != NULL)
stk.push(pLeft);
if(pRight != NULL)
stk.push(pRight);
pNode->left = pRight; //交换左右子女
pNode->right = pLeft;
}
}
return pRoot;
} 问题3:输入一颗二元树,从上往下按层打印树的每个结点,同一层中按照从左往右的顺序打印。
//跟上一篇的镜像二叉树类似
//函数功能 : 按层次遍历二元树
//函数参数 : pRoot指向根结点
//返回值 : 无
void LevelReverse(BSTreeNode *pRoot)
{
if(pRoot == NULL)
return;
queue<BSTreeNode *> nodeQueue;
nodeQueue.push(pRoot);
while(nodeQueue.size())
{
BSTreeNode * pNode = nodeQueue.front(); //取队首元素
nodeQueue.pop(); //必须出队列
if(pNode->left) //左子女
nodeQueue.push(pNode->left);
if(pNode->right) //右子女
nodeQueue.push(pNode->right);
cout<<pNode->value<<' ';
}
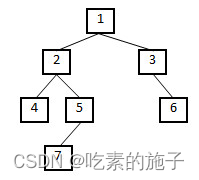
} 问题4:输入一棵二叉树的根结点,判断该树是不是平衡二叉树。如果某二叉树中任意结点的左右子树的深度相差不超过1,那么它就是一棵平衡二叉树。例如下图中的二叉树就是一棵平衡二叉树
struct BinaryTreeNode
{
int data;
BinaryTreeNode *pLeft;
BinaryTreeNode *pRight;
};
//函数功能 : 判断二叉树是不是平衡的
//函数参数 : pRoot为根结点,pDepth为根结点的深度。
//返回值 : 是否平衡的
bool IsBalanced(BinaryTreeNode *pRoot, int *pDepth)
{
if(pRoot == NULL)
{
*pDepth = 0;
return true;
}
int leftDepth, rightDepth; //左右子树的深度
//只有左右子树已经是平衡,才能比较当前节点是不是平衡
if(IsBalanced(pRoot->pLeft, &leftDepth)&&
IsBalanced(pRoot->pRight, &rightDepth))
{
int diff = leftDepth - rightDepth;
if(diff == 0 || diff == 1 || diff == -1) //相差为0或1或-1
{
*pDepth = 1 + (leftDepth > rightDepth ? leftDepth: rightDepth);
return true;
}
else
//如果返回一个false则全盘都是false
return false;
}
return false;
}
