题目
请你为 最不经常使用(LFU)缓存算法设计并实现数据结构。
实现 LFUCache 类:
LFUCache(int capacity) - 用数据结构的容量 capacity 初始化对象
int get(int key) - 如果键 key 存在于缓存中,则获取键的值,否则返回 -1 。
void put(int key, int value) - 如果键 key 已存在,则变更其值;如果键不存在,请插入键值对。当缓存达到其容量 capacity 时,则应该在插入新项之前,移除最不经常使用的项。在此问题中,当存在平局(即两个或更多个键具有相同使用频率)时,应该去除 最近最久未使用 的键。
为了确定最不常使用的键,可以为缓存中的每个键维护一个 使用计数器 。使用计数最小的键是最久未使用的键。
当一个键首次插入到缓存中时,它的使用计数器被设置为 1 (由于 put 操作)。对缓存中的键执行 get 或 put 操作,使用计数器的值将会递增。
函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。
示例:
输入:
["LFUCache", "put", "put", "get", "put", "get", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [3], [4, 4], [1], [3], [4]]
输出:
[null, null, null, 1, null, -1, 3, null, -1, 3, 4]
解释:
// cnt(x) = 键 x 的使用计数
// cache=[] 将显示最后一次使用的顺序(最左边的元素是最近的)
LFUCache lfu = new LFUCache(2);
lfu.put(1, 1); // cache=[1,_], cnt(1)=1
lfu.put(2, 2); // cache=[2,1], cnt(2)=1, cnt(1)=1
lfu.get(1); // 返回 1
// cache=[1,2], cnt(2)=1, cnt(1)=2
lfu.put(3, 3); // 去除键 2 ,因为 cnt(2)=1 ,使用计数最小
// cache=[3,1], cnt(3)=1, cnt(1)=2
lfu.get(2); // 返回 -1(未找到)
lfu.get(3); // 返回 3
// cache=[3,1], cnt(3)=2, cnt(1)=2
lfu.put(4, 4); // 去除键 1 ,1 和 3 的 cnt 相同,但 1 最久未使用
// cache=[4,3], cnt(4)=1, cnt(3)=2
lfu.get(1); // 返回 -1(未找到)
lfu.get(3); // 返回 3
// cache=[3,4], cnt(4)=1, cnt(3)=3
lfu.get(4); // 返回 4
// cache=[3,4], cnt(4)=2, cnt(3)=3
提示:
0 <= capacity <= 104
0 <= key <= 105
0 <= value <= 109
最多调用 2 * 105 次 get 和 put 方法
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/lfu-cache
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
解决思路
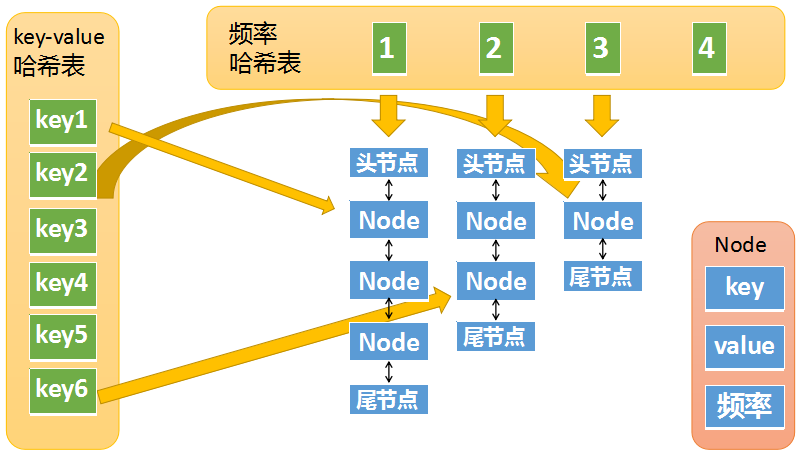
左边哈希表是key-value的哈希表(以下简称kv哈希表)
key就是输入的key,它的value不是一个简单的value,而是一个节点对象。
节点对象Node包含了key,value,以及频率
右边这张哈希表中的key是频率,也就是元素被访问的频率(被访问了1次,被访问了两次等等),它的value是一个双向链表
https://leetcode.cn/problems/lfu-cache/solution/chao-xiang-xi-tu-jie-dong-tu-yan-shi-460-lfuhuan-c/
解决方法
class LFUCache(capacity: Int) {
var mCapacity = capacity
var keyMap = HashMap<Int, Node>()
var frequencyMap = HashMap<Int, LinkedNode>()
var minFrequency = 1
class Node() {
var key = 0
var value = 0
var frequency = 0
var next: Node? = null
var pre: Node? = null
constructor(key: Int, value: Int) : this() {
this.key = key
this.value = value
}
fun insertPre(pre: Node) {
this.pre?.next = pre
pre.pre = this.pre
pre.next = this
this.pre = pre
}
fun insertNext(next: Node) {
this.next?.pre = next
next.next = this.next
this.next = next
next.pre = this
}
fun incrementFrequency(){
frequency++
}
fun remove() {
this.next?.pre = this.pre
this.pre?.next = this.next
}
fun updateValue(value:Int){
this.value = value
}
}
class LinkedNode{
var head = Node()
var tail = Node()
init {
head.next = tail
tail.next = head
}
fun removeLast(){
if (!isEmpty()) {
tail.pre!!.remove()
}
}
fun isEmpty():Boolean{
return head.next == tail
}
fun addNodeAtHead(node : Node){
head.insertNext(node)
}
}
fun get(key: Int): Int {
//不存在返回-1
if (!keyMap.containsKey(key)) {
return -1
} else {
//存在 拿到该节点
val node = keyMap[key]
incrementNode(node!!,false)
return node.value
}
}
fun put(key: Int, value: Int) {
//已经有了key
if (keyMap.containsKey(key)) {
val node = keyMap[key]!!
incrementNode(node,false)
node.value = value
} else {
//不包含
if (mCapacity <= 0){
return
}
//检查容量 不够了删除
if (keyMap.size >= mCapacity) {
//获取最低的频率 移除尾节点
val node = frequencyMap[minFrequency]
val pre = node!!.tail.pre!!
deleteNodeFromLinkedNode(pre)
keyMap.remove(pre.key)
}
//频率是1的存不存在 如果存在直接放到头部
val newNode = Node(key, value)
incrementNode(newNode,true)
keyMap[key] = newNode
}
}
private fun incrementNode(node:Node,newNode : Boolean){
//拿到node
if (newNode) {
node.frequency = 1
minFrequency = 1
}else{
// 从原来的链表中移除
deleteNodeFromLinkedNode(node)
// 频率加1
node.incrementFrequency()
// 如果频率map不包含最低频率 那么最低频率+1
if (!frequencyMap.containsKey(minFrequency)) {
minFrequency++
}
}
insertToLinkedNode(node)
}
// 从原来的链表中移除
private fun deleteNodeFromLinkedNode(node: Node){
val linkedNode = frequencyMap[node.frequency]
node.remove()
if (linkedNode!!.isEmpty()) {
frequencyMap.remove(node.frequency)
}
}
private fun insertToLinkedNode(node: Node): Int {
val frequency = node.frequency
if (frequencyMap.containsKey(frequency)) {
val tempNode = frequencyMap[frequency]!!.head
tempNode.insertNext(node)
} else {
//如果新频率 map 中不存在 则新建
val linkedNode = LinkedNode()
linkedNode.head.insertNext(node)
//放到map里
frequencyMap[frequency] = linkedNode
}
return frequency
}
}
总结
1.写代码之前应该好好规划一下,哪些可以提取出来
不然写的代码一坨,不好维护,不好阅读
第一版本写的,虽然通过,但是重复代码很多
class LFUCache(capacity: Int) {
var mCapacity = capacity
var keyMap = HashMap<Int, Node>()
var frequencyMap = HashMap<Int, Node>()
var minFrequency = 1
var size = 0
class Node() {
var key = 0
var value = 0
var frequency = 0
var next: Node? = null
var pre: Node? = null
constructor(key: Int, value: Int) : this() {
this.key = key
this.value = value
}
fun insertPre(pre: Node) {
this.pre?.next = pre
pre.pre = this.pre
pre.next = this
this.pre = pre
}
fun insertNext(next: Node) {
this.next?.pre = next
next.next = this.next
this.next = next
next.pre = this
}
fun remove() {
this.next?.pre = this.pre
this.pre?.next = this.next
}
}
fun get(key: Int): Int {
//不存在返回-1
if (!keyMap.containsKey(key)) {
return -1
} else {
//存在
//拿到该节点
val node = keyMap[key]
//在原来的频率里面移除
node!!.remove()
//该节点的频率加1
node.frequency++
//频率map不存在新的频率 则创建
if (!frequencyMap.containsKey(node.frequency)){
val newNodeLink = newNodeLink()
newNodeLink.insertNext(node)
frequencyMap[node.frequency] = newNodeLink
}else{
//否则直接放到新频率头部
frequencyMap[node.frequency]!!.insertNext(node)
}
//检查原来的是不是空 是就移除
val old = node.frequency - 1
if (frequencyMap[old]!!.next!!.next == null) {
frequencyMap.remove(old)
}
// 并且检查最低频率是不是还在 不在加1
if (!frequencyMap.containsKey(minFrequency)) {
minFrequency++
}
return node.value
}
}
fun put(key: Int, value: Int) {
//已经有了key
if (keyMap.containsKey(key)) {
//拿到node
val node = keyMap[key]
node!!.value = value
// 从原来的链表中移除
node!!.remove()
// 频率加1
node.frequency++
// 放到对应的map
var frequency = node.frequency
if (frequencyMap.containsKey(frequency)) {
val tempNode = frequencyMap[frequency]
tempNode!!.insertNext(node)
} else {
//如果新频率 map 中不存在 则新建
val newNodeLink = newNodeLink()
newNodeLink.insertNext(node)
//放到map里
frequencyMap[frequency] = newNodeLink
}
frequency--
// 如果链表是空 那么移除该频率的value
val lastNode = frequencyMap[frequency]
if (lastNode!!.next!!.next == null) {
frequencyMap.remove(frequency)
}
// 如果频率map不包含最低频率 那么最低频率+1
if (!frequencyMap.containsKey(minFrequency)) {
minFrequency++
}
} else {
//不包含
if (mCapacity <= 0){
return
}
//检查容量 不够了删除
if (size >= mCapacity) {
//获取最低的频率
// 移除尾节点
var node = frequencyMap[minFrequency]
while (node?.next != null) {
node = node.next
}
val removePre = node?.pre!!
removePre.remove()
keyMap.remove(removePre.key)
// size--
size--
//检查是否为空
if (frequencyMap[minFrequency]!!.next!!.next == null) {
frequencyMap.remove(minFrequency)
}
}
//频率是1的存不存在 如果存在直接放到头部
val newNode = Node(key, value)
newNode.frequency = 1
if (frequencyMap.containsKey(1)) {
val node = frequencyMap[1]
node!!.insertNext(newNode)
} else {
//不存在 创建新的key value 放到头部
val newNodeLink = newNodeLink()
newNodeLink.insertNext(newNode)
frequencyMap[1] = newNodeLink
}
keyMap[key] = newNode
// 最低频率改为1
minFrequency = 1
//长度++
size++
}
}
private fun newNodeLink(): Node {
val head = Node()
val tail = Node()
head.next = tail
tail.pre = head
return head
}
}
