? 最近在学习吴恩达老师的机器学习课程,所以在这里记录一下,主要是完成他的课后作业。
思路:
?1.首先,我们自己编写线性回归函数,看看整个计算的流程;
?2.使用sklearn进行线性回归计算;
?3.对比以上两种方法的优缺点。
1.单变量线性回归:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# 读取文件地址,r将\转义为\\
path = r'C:\Users\Administrator\Desktop\data1.txt'
# 指定哪一行作为表头。默认设置为0(即第一行作为表头),如果没有表头的话,要修改参数,设置header=None
data = pd.read_csv(path, header=None, names=['Population', 'Profit'])
data.head()
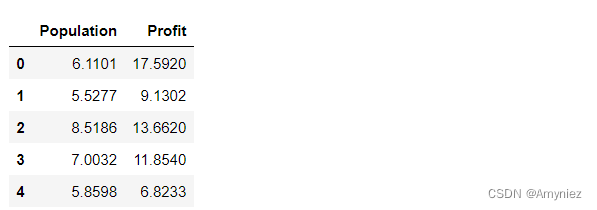
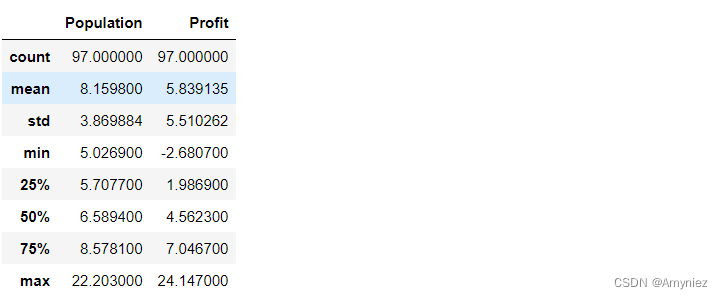
data.describe()
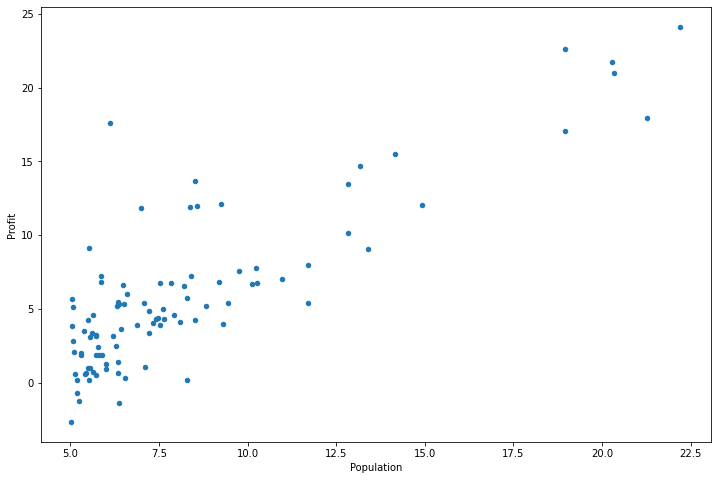
data.plot(kind='scatter', x='Population', y='Profit', figsize=(12,8))# 绘制散点图,figure size为图像大小设置
plt.show()
def computeCost(X, y, theta):
inner = np.power(((X * theta.T) - y), 2)# np.power()函数表示求平方
return np.sum(inner) / (2 * len(X)
data.insert(0, 'Ones', 1) # 在训练集中添加一列,以便可以使用向量化的解决方案来计算代价和梯度
补充:
1、img.shape:(300, 534, 3)
? img.shape[0]:图像的垂直尺寸(高度);对于矩阵来说,表示矩阵的行数,即 300
? img.shape[1]:图像的水平尺寸(宽度);对于矩阵来说,表示矩阵的列数,即 534
? img.shape[2]:图像的通道数,即 3
2、iloc[ : , : ]函数的使用:
? 前面的冒号就是取行数,后面的冒号是取列数
# set X (training data) and y (target variable)
cols = data.shape[1]# 输出矩阵的列数
X = data.iloc[:,0:cols-1]#X是所有行,去掉最后一列,即取Population列
y = data.iloc[:,cols-1:cols]#X是所有行,最后一列,即取Profit列
X.head()# head()是观察前5行
y.head()


# 代价函数是应该是numpy矩阵,所以需要转换X和Y,然后才能使用它们。还需要初始化theta。
# 将X,y转换为矩阵的形式
X = np.matrix(X.values)
y = np.matrix(y.values)
theta = np.matrix(np.array([0,0]))
theta # theta 是一个(1,2)矩阵
X.shape, y.shape, theta.shape #检查一下维度
# ((97, 2), (97, 1), (1, 2))
computeCost(X, y, theta) # 计算代价函数
32.072733877455676
def gradientDescent(X, y, theta, alpha, iters):
temp = np.matrix(np.zeros(theta.shape)) # 生成与theta相同类型的全0矩阵!!!
parameters = int(theta.ravel().shape[1]) # 将theta数组拉平为一维数组,即多维转一维
cost = np.zeros(iters)
for i in range(iters):
error = (X * theta.T) - y
for j in range(parameters):
term = np.multiply(error, X[:,j])
temp[0,j] = theta[0,j] - ((alpha / len(X)) * np.sum(term))
theta = temp
cost[i] = computeCost(X, y, theta)
return theta, cost
补充:
numpy.zeros(shape, dtype=float)使用方法:
? shape: 创建的新数组的形状(维度);
? dtype: 创建新数组的数据类型;如:dtype=np.int32;
? 返回值: 给定维度的全零数组。
# 初始化一些附加变量 :学习速率α和 迭代次数
alpha = 0.01
iters = 1000
# 运行梯度下降算法来将我们的参数θ适合于训练集
g, cost = gradientDescent(X, y, theta, alpha, iters)
g
matrix([[-3.24140214, 1.1272942 ]])
# 使用拟合的参数计算训练模型的代价函数(误差)
computeCost(X, y, g)
4.515955503078914
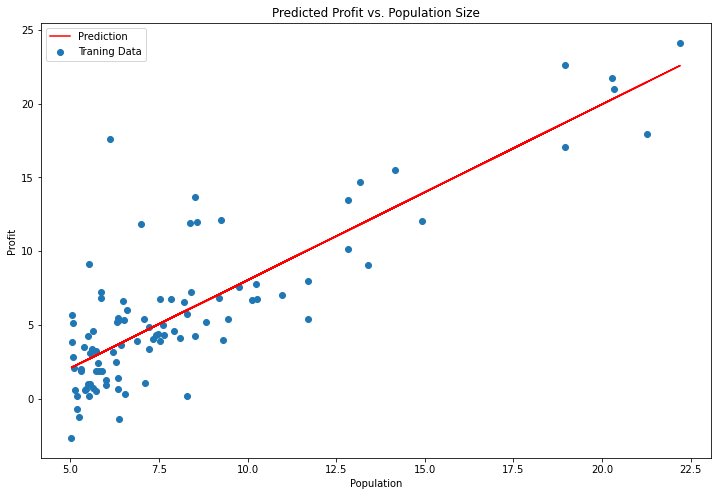
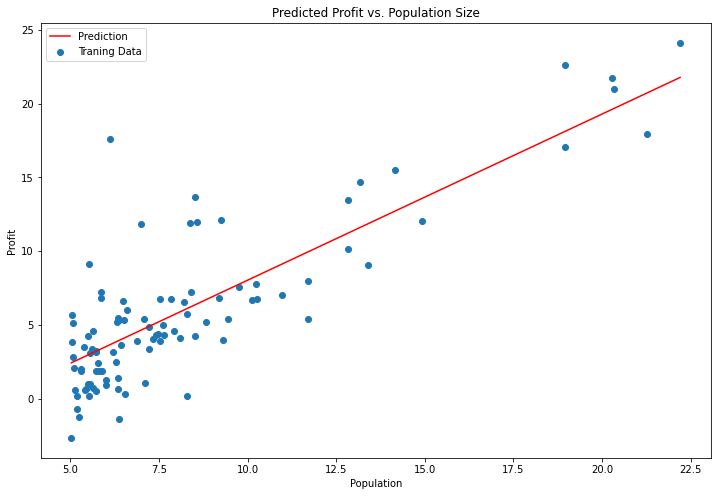
# 绘制线性模型以及数据
x = np.linspace(data.Population.min(), data.Population.max(), 100)
f = g[0, 0] + (g[0, 1] * x)
fig, ax = plt.subplots(figsize=(12,8))
ax.plot(x, f, 'r', label='Prediction')
ax.scatter(data.Population, data.Profit, label='Traning Data')
ax.legend(loc=2)
ax.set_xlabel('Population')
ax.set_ylabel('Profit')
ax.set_title('Predicted Profit vs. Population Size')
plt.show()
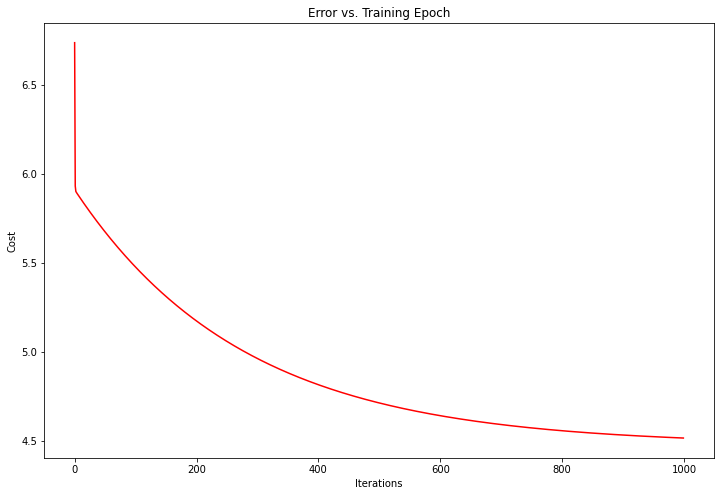
# 代价总是降低 - 这是凸优化问题的一个例子
fig, ax = plt.subplots(figsize=(12,8))
ax.plot(np.arange(iters), cost, 'r')
ax.set_xlabel('Iterations')
ax.set_ylabel('Cost')
ax.set_title('Error vs. Training Epoch')
plt.show()
2.多变量线性回归
path = r'C:\Users\Administrator\Desktop\house prise.txt'
data2 = pd.read_csv(path, header=None, names=['Size', 'Bedrooms', 'Price'])
data2.head()

# 特殊归一化处理
data2 = (data2 - data2.mean()) / data2.std()
data2.head()
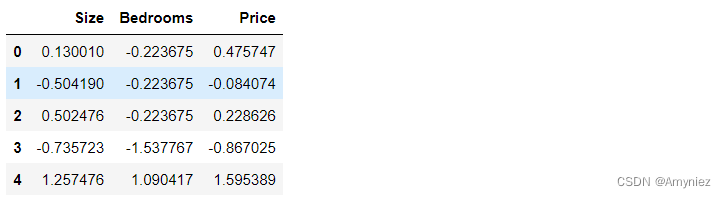
# 按照例子1的方法进行数据处理
# add ones column
data2.insert(0, 'Ones', 1)
# set X (training data) and y (target variable)
cols = data2.shape[1]
X2 = data2.iloc[:,0:cols-1]
y2 = data2.iloc[:,cols-1:cols]
# convert to matrices and initialize theta
X2 = np.matrix(X2.values)
y2 = np.matrix(y2.values)
theta2 = np.matrix(np.array([0,0,0]))
# perform linear regression on the data set
g2, cost2 = gradientDescent(X2, y2, theta2, alpha, iters)
# get the cost (error) of the model
computeCost(X2, y2, g2)
0.1307033696077189
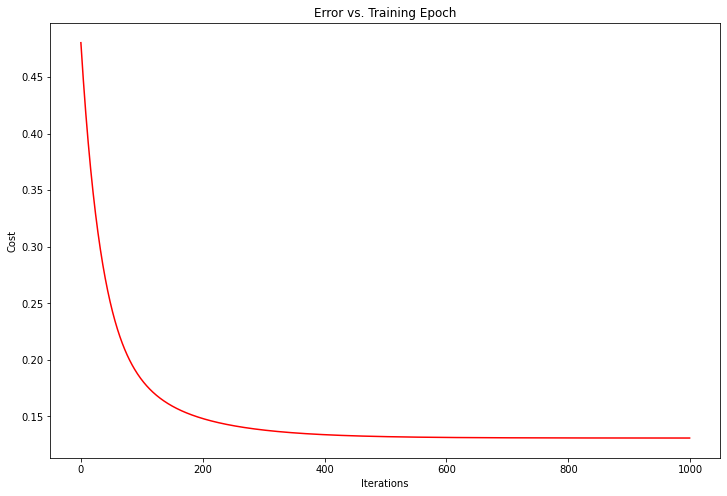
此处的代价函数更小
# 查看训练进程
fig, ax = plt.subplots(figsize=(12,8))
ax.plot(np.arange(iters), cost2, 'r')
ax.set_xlabel('Iterations')
ax.set_ylabel('Cost')
ax.set_title('Error vs. Training Epoch')
plt.show()
# 使用scikit-learn的线性回归函数,而不是从头开始实现这些算法
from sklearn import linear_model
model = linear_model.LinearRegression()
model.fit(X, y)
# scikit-learn model的预测表现
x = np.array(X[:, 1].A1)
f = model.predict(X).flatten()
fig, ax = plt.subplots(figsize=(12,8))
ax.plot(x, f, 'r', label='Prediction')
ax.scatter(data.Population, data.Profit, label='Traning Data')
ax.legend(loc=2)
ax.set_xlabel('Population')
ax.set_ylabel('Profit')
ax.set_title('Predicted Profit vs. Population Size')
plt.show()