第五章 二叉树非递归遍历
先序遍历
先遍历根节点其次左子树和右子树
中序遍历
先遍历左子树其次根节点最后右子树
后序遍历
先左子树再右子树最后根节点
还是上个博客的图

先序遍历结果
1 2 4 6 3 5 (根左右)
1是根 2 4 6 是左子树 3 5 是右子树
中序遍历结果
2 6 4 1 3 5 (左根右)
2 6 4 是左子树 1 是根 3 5 是右子树
后序遍历结果
6 4 2 5 3 1 (左右根)
6 4 2 是左子树 5 3 是右子树 1 是根
今天用栈来实现非递归遍历
非递归VS递归
递归一般比较好像容易实现
但是占用空间资源比较多,递归的层次越多,资源占用越大。
非递归就比较难实现,同时还要依托栈来实现。但空间利用高一点。运行时间也会相较递归短很多。
先序遍历
根左右
先访问根节点,同时压栈。纵深左子树(先访问后压栈),当左子树空了,退栈纵深右子树(先访问后压栈)。直至没有节点同时栈空。
//先序遍历(非递归)
void PreOrder2(BiTree T){
Stack S=(Stack)malloc(sizeof(struct stack));
Initstack(S);//初始化栈
BiTree p=T;//指向树的根节点
while(p||!isEmpty(S)){//栈不空或p不空时循环
if(p){
printf("%c ",p->data);//访问节点
push(S,p);//入栈
p=p->lchild;//左子树不空的话,纵深左子树
}
else{//出栈,转向右子树
pop(S,p);
p=p->rchild;
}
}
free(S);
}
中序遍历
左根右
第一步,纵深左子树,同时压栈。直至左孩子为空了,说明这是可以访问的节点了。
第二步,退栈并访问,检查是否有右孩子。若右孩子为空,继续执行第二步。若存在右孩子,转向右子树执行第一步。
//中序遍历(非递归)
void InOrder2(BiTree T){
Stack S=(Stack)malloc(sizeof(struct stack));
Initstack(S);//初始化栈
BiTree p=T;//指向树的根节点
while(p||!isEmpty(S)){//栈不空或p不空时循环
if(p){//压栈,纵深左子树
push(S,p);
p=p->lchild;
}
else{//退栈,访问,检查右子树
pop(S,p);
printf("%c ",p->data);
p=p->rchild;
}
}
free(S);
}
后序遍历
左右根
第一步,沿着根的左孩子依次入栈,直至左孩子为空。
第二步,读栈顶元素,若其右孩子不空且被未被访问过,转向右子树执行第一步。否则,出栈并访问。
//后序遍历(非递归)
void PostOrder2(BiTree T){
Stack S=(Stack)malloc(sizeof(struct stack));
Initstack(S);//初始化栈
BiTree p=T;//指向树的根节点,充当遍历指针
BiTree r=NULL;//r指向上一次被访问的节点,辅助判断
while(p||!isEmpty(S)){//栈不空或p不空时循环
if(p){//压栈,纵深左子树
push(S,p);
p=p->lchild;
}
else{
GetTop(S,p);//读栈顶元素
if(p->rchild&&p->rchild!=r)//若栈顶元素有右孩子并且未被访问
p=p->rchild;//转向右子树
else{//若栈顶元素没有右孩子或被访问了
pop(S,p);//退栈
printf("%c ",p->data);//访问
r=p;//r指向上一次被访问的节点,辅助判断
p=NULL;
}
}
}
free(S);
}
贴一下完整的代码
包含了栈的定义,出入栈,访问栈顶元素等。
使用了带头结点的链栈。出栈入栈容易实现和理解!之前的稿子也写了几次栈了,这里的代码就不详细注释了。
#include<stdio.h>
#include<stdlib.h>
//定义树节点
typedef struct BiNode{
char data;//数据域
//指针域,分别指向左孩子和右孩子
struct BiNode *lchild,*rchild;
}BiTNode,*BiTree;
//定义栈节点
typedef struct stack{
BiTree data;//栈顶数据域是指向树节点的指针;
struct stack *next;
}stack,*Stack;
//初始化栈
bool Initstack(Stack &S){
S->next=NULL;
return true;
}
//入栈
bool push(Stack &S,BiTree p){
Stack q=(Stack)malloc(sizeof(struct stack));
q->data=p;
q->next=S->next;
S->next=q;
return true;
}
//出栈
bool pop(Stack &S,BiTree &p){
if(S->next==NULL) return false;
Stack q=S->next;
S->next=q->next;
p=q->data;
free(q);
return true;
}
//访问栈顶元素
bool GetTop(Stack &S,BiTree &p){
if(S->next==NULL) return false;
Stack q=S->next;
p=q->data;
return true;
}
//判断是否为空栈
bool isEmpty(Stack S){
if(S->next==NULL) return true;
else return false;
}
//创建一棵树,先序创建
void CreateTree(BiTree &T){
char ch;//存放输入值
scanf("%c\n",&ch);
if(ch=='#')
T=NULL;
else
{
T=(BiTree)malloc(sizeof(BiNode));
T->data=ch;
CreateTree(T->lchild);
CreateTree(T->rchild);
}
}
//先序遍历(递归)
void PreOrder(BiTree T){
if(T!=NULL){
if(T->data!='#')//访问当前节点
printf("%c ",T->data);
PreOrder(T->lchild);//遍历左子树
PreOrder(T->rchild);//遍历右子树
}
}
//先序遍历(非递归)
void PreOrder2(BiTree T){
Stack S=(Stack)malloc(sizeof(struct stack));
Initstack(S);
BiTree p=T;
while(p||!isEmpty(S)){
if(p){
printf("%c ",p->data);
push(S,p);
p=p->lchild;
}
else{
pop(S,p);
p=p->rchild;
}
}
free(S);
}
//中序遍历(递归)
void InOrder(BiTree T){
if(T!=NULL){
InOrder(T->lchild);//遍历左子树
if(T->data!='#')//访问当前节点
printf("%c ",T->data);
InOrder(T->rchild);//遍历右子树
}
}
//中序遍历(非递归)
void InOrder2(BiTree T){
Stack S=(Stack)malloc(sizeof(struct stack));
Initstack(S);
BiTree p=T;
while(p||!isEmpty(S)){
if(p){
push(S,p);
p=p->lchild;
}
else{
pop(S,p);
printf("%c ",p->data);
p=p->rchild;
}
}
free(S);
}
//后序遍历
void PostOrder(BiTree T){
if(T!=NULL){
PostOrder(T->lchild);//遍历左子树
PostOrder(T->rchild);//遍历右子树
if(T->data!='#')//访问当前节点
printf("%c ",T->data);
}
}
//后序遍历(非递归)
void PostOrder2(BiTree T){
Stack S=(Stack)malloc(sizeof(struct stack));
Initstack(S);
BiTree p=T;
BiTree r=NULL;
while(p||!isEmpty(S)){
if(p){
push(S,p);
p=p->lchild;
}
else{
GetTop(S,p);
if(p->rchild&&p->rchild!=r)
p=p->rchild;
else{
pop(S,p);
printf("%c ",p->data);
r=p;
p=NULL;
}
}
}
free(S);
}
int main(){
BiTree T;
CreateTree(T);
printf("先序遍历: ");
PreOrder(T);
printf("\n中序遍历: ");
InOrder(T);
printf("\n后序遍历: ");
PostOrder(T);
printf("\n非递归先序遍历:");
PreOrder2(T);
printf("\n非递归中序遍历:");
InOrder2(T);
printf("\n非递归后序遍历:");
PostOrder2(T);
return 0;
}
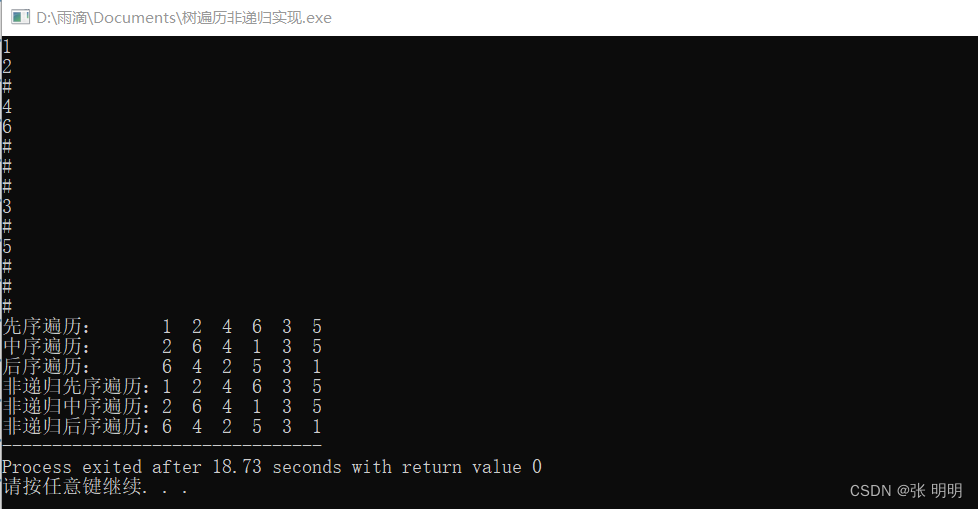
结果展示