队列
这个队伍在计算机的世界里叫做 队列 ,第一个同学叫做队首,最后一个同学叫做队尾。队首的同学买好饭离开叫做出队,刚来的人加入末尾叫做入队。队列有一个很重要的性质,就是 先进先出 ,First In First Out(FIFO)。
什么叫先进先出呢?通俗的说就是先来的同学一定先打到饭。具体来说就是,每个同学在刚开始加入队伍的时候都必须站在队列的一端(对于打饭的情况来说,就是站在队列的最后一位),而队伍的另一端的同学第一个去打饭;而且在排队过程中不允许两个同学交换顺序。因为有了不允许插队的限制,所以总是先来排队的同学先能够买到饭然后先离开队列,而不会出现后面的同学先买饭离开的情况。
由于队列先进先出的特殊性质,我们在构造它时,需要用两个变量来代表队首和队尾的位置,设置这两个变量有利于我们去维护队列的次序性。在构造函数中,我们会将队首标记置为 0,将队尾标记置为?1,并给队列分配内存空间。而在析构函数中,我们只要把分配给队列的数组空间释放。
接下来我们来学习队列的插入操作。我们在构造队列时,定义了一个队尾标记,在执行入队操作时,只需一直更新队尾标记就能保持好队列元素间的先后关系。
队列插入操作的实现方法如下:
1. 判断队列是否已满。实际上是由于队尾标记不断增加,需要判断队尾标记是否大于数组长度。
2. 更新队尾标记,将新插入元素存入队尾。
如:当前有一个包含元素 1、 2、 3 的队列,此时队尾标记为 2。我们要往队列中插入一个元素 4。
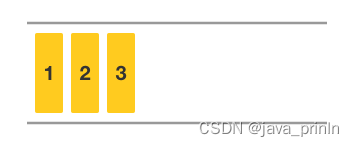
入队时,根据先进先出的性质我们会将新元素放在队尾。

将队尾标记加 1,接着存入新元素就完成了整个入队操作。此时队尾标记为 3。
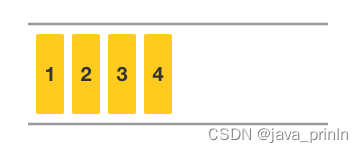
队列在遍历时也是依靠队首和队尾标记,我们只需把从队首标记上到队尾标记上的元素依次输出就好了。
队列遍历操作的实现方法如下:
1. 输出队首标记所在的元素。
2. 队首标记后移一位。
3. 若队尾标记和队首标记相等,输出最后一个元素,否则返回步骤 1。
队列入队是通过更新队尾标记实现的,那么出队操作又该怎么做呢?
队列出队操作的实现方法如下:
1. 比较队尾标记和队首标记的大小,当队首标记大于队尾标记则说明队列为空了,此时出队操作是非法的。
2. 令队首标记后移一位,队首标记后移即视作原队首出队了。
还是利用刚刚的队列来演示。此时队列中有 1、2、3、 4 四个元素。
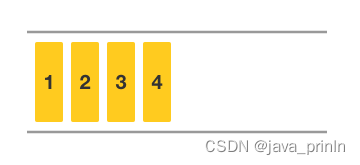
当前队首元素为 1,队首标记为 0。
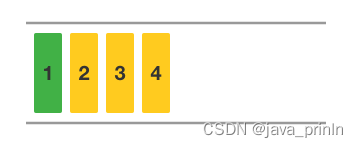
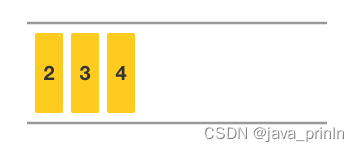
将队首标记后移一位就移除了队首元素。此时队首元素为 2,队首标记为 1。
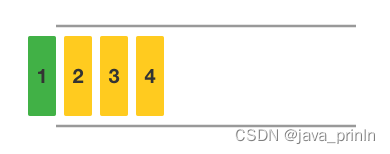
这样就完成了整个出队过程。
创建队列
#include <stdio.h>
#include <stdlib.h>
// 请在下面实现队列 Queue
// 定义一个空的结构体 Queue, 作为我们队列的数据结构类型。
// 接下来在结构体中定义一个 int 类型的指针变量 data, 用来保存队列中每个元素的编号。
// 定义 三个 int 变量 head. tail, length. head 和tail 分别表示队列的一个元素(队首)和 最后一个元素(队尾) 在数组中的位置,length 用于记录数组的长度。
// 我们队列中的所有元素都是介于head 和 tail 的位置之间, 并且是连续存放的。
typedef struct Queue {
int *data;
int head, tail,length;
}Queue;
// 定义一个初始化函数 init , 函数没有返回值, 参数为 Queue 类型的指针变量q, int 类型的变量length, 表示准备给队列q 中的data 数组动态分配 length 个int 类型的数据。
void init(Queue *q, int length) {
// 首先先给 q->data 数组分配 length 个 int 类型的内存, 然后将length 的值赋给 q->length. 使用malloc 来动态分配内存。
q->data = (int *)malloc(sizeof(int) *length);
q->lenght = length;
// 初始队列为空, 所以这里我们将队首元素, q->head 设置为0,再将队尾标记为 q->tail 设置为 -1.
q->head = 0;
q->tail = -1;
}
// 需要在程序结束前释放对垒所占用的内存,参数为Queue 类型的指针变量 q.
// 在 clear 函数中, 我们要释放q->data 和 q 指向的内存空间, 使用free
void clear(Queue *q) {
free(q->data);
free(q);
}
int main() {
// 在主函数里定义一个Queue 的指针queue , 并动态申请一个Queue 大小的空间。然后调用初始化函数init 完成初始化操作, 参数为queue 和初始化队列的长度,这里设为100.
Queue *q = (Queue *)malloc(sizeof(Queue));
init(queue, 100);
clear(queue);
return 0;
}
加入队列
#include <stdio.h>
#include <stdlib.h>
#define ERROR 0
#define OK 1
typedef struct Queeu {
int *data;
int head, tail, length;
}Queue;
void init(Queue *q, int length) {
q->data = (int *)malloc(sizeof(int) * length);
q->length = length;
q->head = 0;
q->tail = -1;
}
// 请在下面实现插入函数 push
// 首先要定义队列的插入函数,在clear 函数前定义一个 返回值为int 类型的函数push(), 参数有两个,一个是Queue 类型的指针参数q, 另一个是int 类型的变量 element,
// 接下来我们要实现队列的插入函数
// 在插入时我们确保队列中还有位置能够插入。我们可以使用一个if 语句来判断, 若队列已满,则返回ERROR, 我们已经将ERROR 定义为0, 将OK 定义为1 了。
// 在这里, 写在if 语句中放入条件显然是 q->tail +1 大于等于 q->length , 满足条件返回ERROR。
int push(Queue *q, int element) {
if(q->tail+1 >= q->length) {
return ERROR;
}
// 接下来,实现队列的插入,先将队尾标记q->tail 往后加一位,然后将元素 element 放到队尾,最后返回OK 结束。
q->tail++;
q->data[q->tail] = element;
return OK;
}
void clear(Queue *q) {
free(q->data);
free(q);
}
int main() {
Queue *queue = (Queue *)malloc(sizeof(Queue));
init(queue, 100);
// 请在主函数里写一个 for 循环,依次将1 到 10 十个数字调用插入函数插入到队列queue 里(借用i 变量,i 从1 循环到10).
for(int i = 1; i <=10; i++) {
push(queue, i);
}
clear(queue);
return 0;
}
队列遍历
#include <stdio.h>
#include <stdlib.h>
#define ERROR 0
#define OK 1
typedef struct Queue {
int *data;
int head, tail, length;
}Queue;
void init(Queue *q, int length) {
q->data = (int *)malloc(sizeof(int) * length);
q->length = length;
q->head = 0;
q->tail = -1;
}
int push(Queue *q, int element) {
if(q->tail + 1 >= q->length) {
return ERROR;
}
q->tail++;
q->data[q->tail] = element;
return OK;
}
// 请在下面实现输出函数 output
void output(Queue *q) {
for(int i = q->head; i <= q->tail; i++) {
printf("%d ",q->data[i]);
}
printf("\n");
}
void clear(Queue *q) {
free(q->data);
free(q);
}
int main() {
Queue *queue = (Queue *)malloc(sizeof(Queue));
init(queue, 100);
for (int i = 1; i <= 10; i++) {
push(queue, i);
}
output(queue);
clear(queue);
return 0;
}
队列中谁是第一名
#include <stdio.h>
#include <stdlib.h>
#define ERROR 0
#define OK 1
typedef struct Queue {
int *data;
int head, tail, length;
}Queue;
void init(Queue *q, int length) {
q->data = (int *)malloc(sizeof(int) * length);
q->length = length;
q->head = 0;
q->tail = -1;
}
int push(Queue *q, int element) {
if(q->tail + 1 >= q->length) {
return ERROR;
}
q->tail++;
q->data[q->tail] = element;
return OK;
}
void output(Queue *q) {
for (int i = q->head; i <= q->tail; i++) {
printf("%d ", q->data[i]);
}
printf("\n");
}
// 请在下面实现队首元素输出函数 front,
// 我们首先来是宪法队列的队首元素输出函数
定义一个返回值为 int 类型,只有一个Queue 类型的指针参数q 的函数 front ,
// 队首元素值q->head 对应的元素, 我们直接在front 函数中返回它就可以。
int front(Queue *q) {
return q->data[q->head];
}
// 请在下面实现删除队首元素函数 pop
// 请在 front 函数后面定义一个没有返回值,只有一个 Queue 类型的指针参数 q 的函数 pop().
// 在 pop 函数中 把 q->head 标记往后移一位就表示删除队首元素了。
void pop(Queue *q) {
q->head++;
}
// 请在下面实现判断队列是否为空的函数 empty
// 目前我们已经实现了 队首元素输出函数,
// 在输出队首元素之前,我们必须保证队列不为空, 这里我们用一个函数empty 来实现。
// 函数返回值类型为 int ,参数为Queue 类型的指针变量q。
// 在empty 函数中,我们可以通过队首标记和队尾标记大小来判断队列是否为空。
// 如果队首标记大于 队尾标记,则队列为空,我们直接把他们的比较结果返回就可以。
int empty(Queue *q) {
return q->head > q->tail;
}
void clear(Queue *q) {
free(q->data);
free(q);
}
int main() {
Queue *queue = (Queue *)malloc(sizeof(Queue));
init(queue, 100);
for (int i = 1; i <= 10; i++) {
push(queue, i);
}
output(queue);
// 在此之前,需要先调用 empty 函数确保队列不为空,我们可以用 if 语句来实现它,这里简单的写法我们直接让 if 语句 来实现它, 这里简单的写法 我们直接让 if 语句的条件为 !empty(queue) 就可以了。
// 接下来 我们就可以 调用 front 函数, 输出当前队列queue 的队首元素, 为了美观,再多输出一个换行。
// 接下来我们实现删除队首元素函数
// 现在我们在主函数里调用它,同样,在删除队首元素时, 我们也要确保 队列不为空 。
if(!empty(queue)) {
printf("%d\n", front(queue));
pop(queue);
}
// 最后我们调用output 函数把队列中所有元素输出。
output(queue);
clear(queue);
return 0;
}
循环队列
假上溢 。
什么叫“假上溢”呢?回忆一下之前的插入队列的代码:
tail++;
data[tail] = element;
}
当tail达到队列的上限后就不能再插入了,此时再插入就意味着溢出。但是tail达到上限后就意味着要插入的元素真的“无处可放”了么?
我们再来回忆一下删除队首元素的操作。
我们一起来看一遍代码:
head++;
如果一个队列在不断的执行插入、弹出、插入、弹出…那么可以想象,当执行到tail达到队列上限之后,便不能再插入到队列中了,而此时队列其实是空的。
我们该如何解决这个问题呢?
接下来我们会介绍一种目前使用最多的方法:循环队列。
循环队列,顾名思义,就是以循环的方式来存储队列。当队尾标记tail到达队列上限后,如果队列内的元素没有达到上限,就跳转到数组的开始位置,也就是 0 的位置,队首标记到达队列上限也采取同样的处理。通过这样的方法,我们就能够最大化利用内存空间,避免“假上溢”的情况出现。
循环队列的入队和遍历
#include <stdio.h>
#include <stdlib.h>
#define ERROR 0
#define OK 1
// 首先我们给Queue 类增加一个成员 count. 这个成员用来存储当前循环队列一共有多少元素,
typedef struct Queue {
int *data;
int head, tail, length, count;
} Queue;
// 接下来 我们要对 count 成员变量进行初始化
请在 init 初始化函数最后一行 写出合适的 对 count 初始化的代码。
void init(Queue *q, int length) {
q->data = (int *)malloc(sizeof(int) * length);
q->length = length;
q->head = 0;
q->tail = -1;
q->count = 0;
}
// 接下来 我们要修改队列的入队 push 函数。
// 在进入入队操作时,首先要判断队列是否已经满了。 那么循环队列怎么判断队列是否 已经满了
// 不同于一般队列,当循环队列q 的 tail 已经指向数组的最后, 而队列曾经有若干次出队操作导致head 不在 最初的位置, 此时时可以进行队列操作的, 我们会将这个元素插入到数组开始位置。
// 总之,在循环队列q 中 我们不能通过 tail 的位置 判断队列是否已满了,还记得我们 刚刚定义的 count 变量么,这时候它就派上用场。 如果当前队列中的元素数量加上现在即将要入队的元素不会超过 队列的总容量,那么队列此时就没有满,可以进行入队操作。
// 当判断出队列未满后,我们要首先调整 tail 的值
// tail 在增加 1 之后, 需要对容量length 取模, 就能获得这次入队的元素要插入的位置了。
// 当每次入队操作后,队列里的元素数量都会发生变化,那么应该更新队列内元素数量。
// 请在push 函数里 写下跟新 q->count 的操作。
int push(Queue *q, int element) {
if(q->count >= q->length) {
return ERROR;
}
q->tail = (q->tail + 1) % q->length;
q->data[q->tail] = element;
q->count ++;
return OK;
}
// 对于之前一般的队列, 我们只需要从head 遍历到 tail 就可以了, 因为当队列非空的时候,tail 一定不会比head 小。但是对于非空的循环队列,tail 是有可能出现在 head 的左侧的。
// 当我们从head 开始向右遍历时,如果走到了队尾而又没有和 tail 的值相等,则将 当前遍历的下标对length 取模就可以了;当从 length -1 向下一个位置移动时,会移动到 0 而非 length. 直到下标和tail 相等时,我们就算完成了 队列的遍历输出。
// 首先,在output 函数内的第一行,定义一个 int 类型的下标变量 i, 初始值等于q->head.
// 接下来 我们用一个 do-while 来完成循环队列的遍历和输出。
// 我们来想一下 如何写循环的终止条件,下标i 不能 等于循环队列里最后一个元素的下一个位置, 我们知道tail 所对应的即使最后一个元素,那么它的下一个位置 应该是什么呢,
答案应该是 (q->tail + 1) % q->length , 别忘记对 q->length 进行取余. 这里我们先把 do-while 的框架写好。
// 在循环里,首先我们把当前下标 i 对应的元素q->data[i] 输出吧, 元素后面跟 一个空格, 接着我们下标 i 一道下一个 位置, 记得把下标 i 对q->length 取余。
void output(Queue *q) {
int i = q->head;
do {
printf("%d ", q->data[i]);
i = (i + 1) % q->length;
} while(i != (q ->tail + 1) % q->length);
printf("\n");
}
void clear(Queue *q) {
free(q->data);
free(q);
}
int main() {
Queue *queue = (Queue *)malloc(sizeof(Queue));
init(queue, 100);
for (int i = 1; i <= 10; i++) {
push(queue, i);
}
output(queue);
clear(queue);
return 0;
}
循环队列的出队操作
#include <stdio.h>
#include <stdlib.h>
#define ERROR 0
#define OK 1
typedef struct Queue {
int *data;
int head, tail, length, count;
}Queue;
void init(Queue *q, int length) {
q->data = (int *)malloc(sizeof(int) * length);
q->length = length;
q->head = 0;
q->tail = -1;
q->count = 0;
}
// 我们之前说过,无论是head 还是 tail d, 当他们从数组的最后一位向后移动时,都要移动到第一位,也就是下标为0 的位置。对于队列来说,在进行出队操作时,head ++ 已经足够了,但是对循环队列来说是不行的,我们还需要让 它对 q->length 取余 。
// 在元素出队之后,我们还要更新count。每次出队时,让count 减一。
// 我们之前实现的队列,在empty 函数中利用 head d和 tail 的 大小关系来判断队列是否为空,
// 但是对于循环队列来说,不能用同样的函数来判断队列是否为空了, 因为非空循环队列的 tail 是由可能在head 的前面的。
// 我们在push 操作时用 count 来判断队列是否以满. 对于空队列来说, count 的值为0 因此我们只需要 在 empty 函数中, 将返回值成为count 等于 0.
int push(Queue *q, int element) {
if (q->count >= q->length) {
return ERROR;
}
q->tail = (q->tail + 1) % q->length;
q->data[q->tail] = element;
q->count++;
return OK;
}
void output(Queue *q) {
int i = q->head;
do {
printf("%d ", q->data[i]);
i = (i + 1) % q->length;
} while(i != (q->tail + 1) % q->length);
printf("\n");
}
int front(Queue *q) {
return q->data[q->head];
}
void pop(Queue *q) {
q->head = (q->head + 1) % q->length;
q->count--;
}
int empty(Queue *q) {
return q->count == 0;
}
void clear(Queue *q) {
free(q->data);
free(q);
}
int main() {
Queue *q = (Queue *)malloc(sizeof(Queue));
init(q, 100);
for (int i = 1; i <= 10; i++) {
push(q, i);
}
output(q);
if (!empty(q)) {
printf("%d\n", front(q));
pop(q);
}
output(q);
clear(q);
return 0;
}
