
斐波那契数列
普通的代码:

将数组压缩,使用滚动的方式缩小空间:

而此处如果使用递归的话时间复杂度是O(2^n)(为什么?)
?而空间复杂度:O(n) 算上了编程语?中实现递归的系统栈所占空间

此处的时间复杂度的思考,参照通过一道面试题目,讲一讲递归算法的时间复杂度! (qq.com)
来看求一个数的n次方,看下面这几段代码的时间复杂度:
递归算法的时间复杂度本质上是要看:?「递归的次数 * 每次递归中的操作次数」。
int function2(int x, int n) {
if (n == 0) {
return 1; // return 1 同样是因为0次方是等于1的
}
return function2(x, n - 1) * x;
}function2是递归,递归了n次,时间复杂度为O(n)
int function3(int x, int n) {
if (n == 0) {
return 1;
}
if (n % 2 == 1) {
return function3(x, n / 2) * function3(x, n / 2)*x;
}
return function3(x, n / 2) * function3(x, n / 2);
}
function3,我们来分析一下,首先看递归了多少次呢,可以把递归抽象出一颗满二叉树。刚刚同学写的这个算法,可以用一颗满二叉树来表示(为了方便表示,选择n为偶数16),如图:
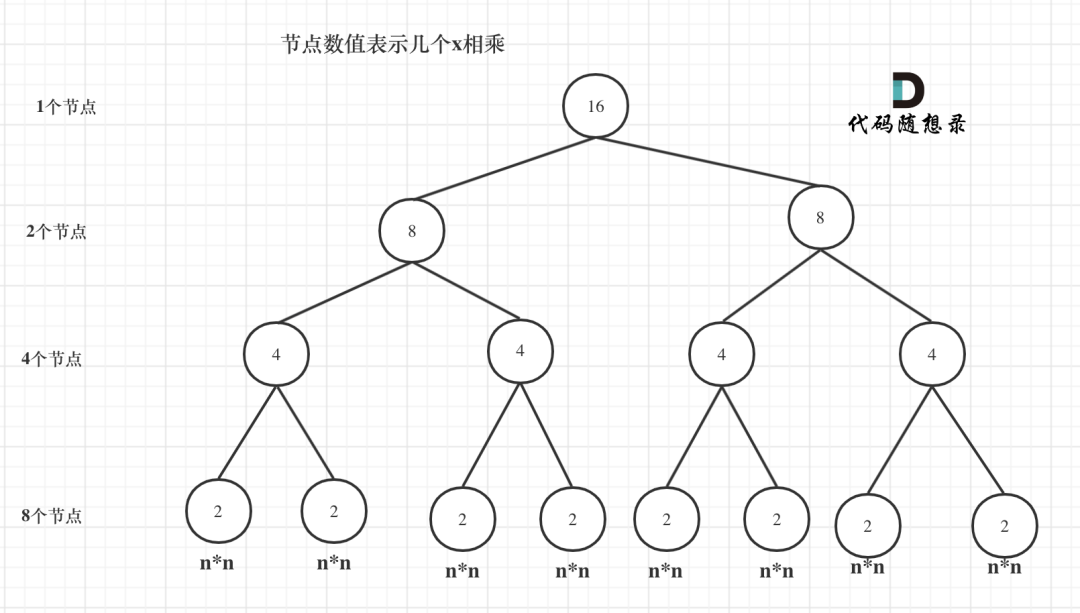
总共n-1个结点时间复杂度为O(n)
int?function4(int?x,?int?n)?{
????if?(n?==?0)?{
????????return?1;
????}
????int?t?=?function4(x,?n?/?2);//?这里相对于function3,是把这个递归操作抽取出来
????if?(n?%?2?==?1)?{
????????return?t?*?t?*?x;
????}
????return?t?*?t;
}
此处将代码在3的基础上改改,每次只调用一次递归,则此时调用递归的次数为树的深度,即为logn,时间复杂度即为O(logn)
再来看看前面的求斐波那契数列的递归法时间复杂度为什么是O(2^n)?
数学解法:
递归算法的时间复杂度,记计算第n个数的所需时间为T(n),那么T(n) = T(n-1) + T(n-2) ,由T(n-1) > T(n-2) 可以推出T(n) < 2T(n-1) < 2^2 * T(n-2)<2^(n-1)T(1),可以推出T(n)的时间复杂度为O(2^n)。
爬楼梯及其拓展
根据dp[i]代表到第i层有几种方法,我们让i从1开始,舍弃dp[0],不考虑其意义。
代码很好写

重点是扩展:
这道题?还可以继续深化,就是?步?个台阶,两个台阶,三个台阶,直到 m个台阶,有多少种?法爬 到n阶楼顶。
这?有难度了,这其实是?个完全背包问题,但?扣上没有这种题?,所以后续我在讲解背包问题的时 候,今天这道题还会拿从背包问题的?度上来再讲?遍。
其实就是对于dp[8],那么假如可以一次爬1个、2个、3个、4个台阶的话。
那么dp[8]的值就等于dp[8-1]+dp[8-2]+dp[8-3]+dp[8-4]。
所以代码如下:

?
扩展2:力扣746:

?

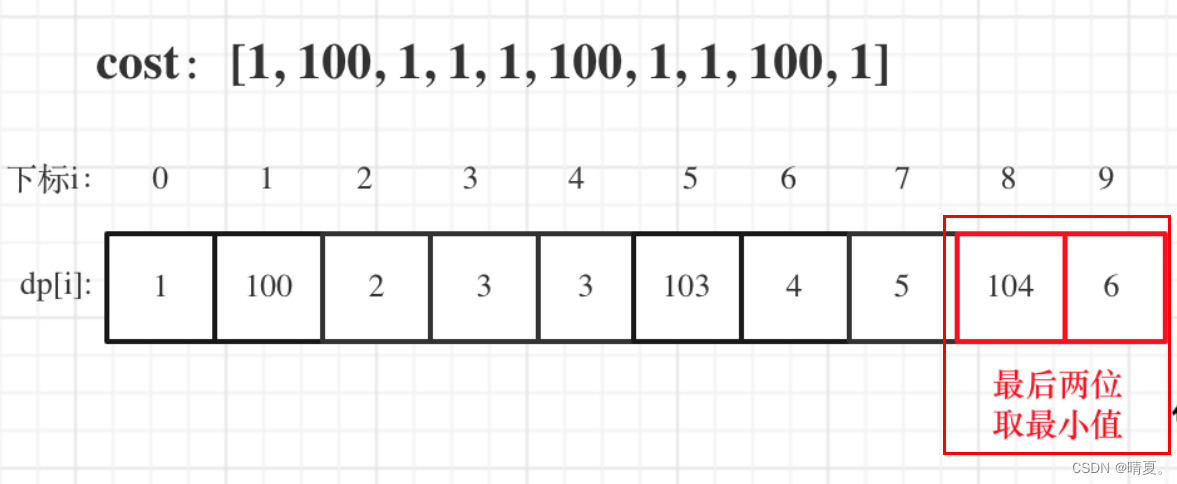
dp[i]代表的是到第i层所花费的最小代价,并且支付了费用,然后可以往上走一或两层。
也就是说最后想走到第n层,是不需要付第n层的费用的。也就是说最后的返回值是min(dp[n-1],dp[n-2])。
另外这里下标它说从0开始,那就从0开始写,当然可以从1开始。
转移方程:
dp[i] = min(dp[i - 1], dp[i - 2]) + cost[i];
?代码:

不同路径
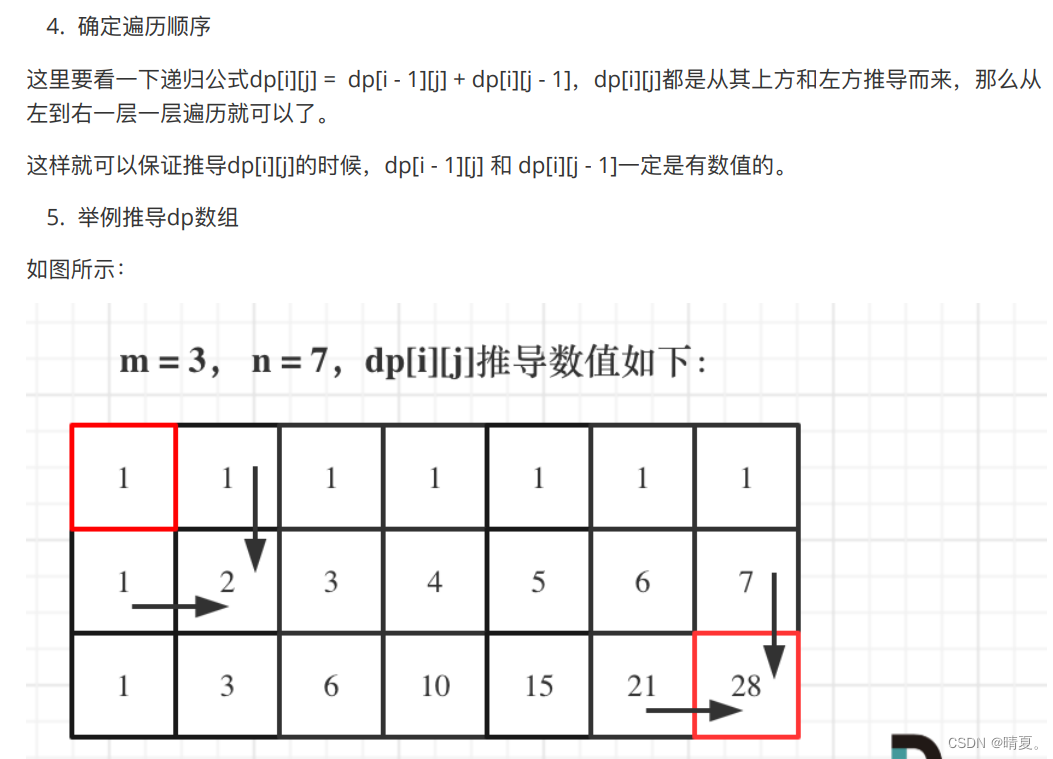
力扣 (leetcode.cn) https://leetcode.cn/problems/unique-paths/
https://leetcode.cn/problems/unique-paths/
递归方法当然好写,不过其时间复杂度如何计算?
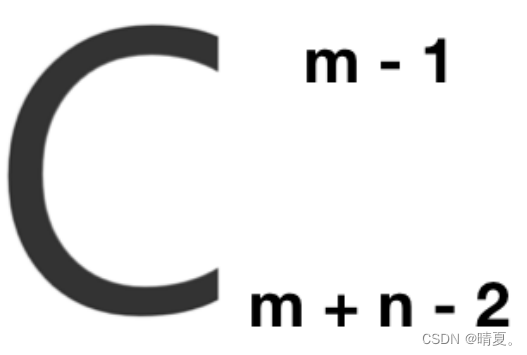
由于其只能往右或者下走,则走过的长度是确定的,即m+n-1,每一步都有两种选择,所以时间复杂度是O(2^(m+n-1))?
?

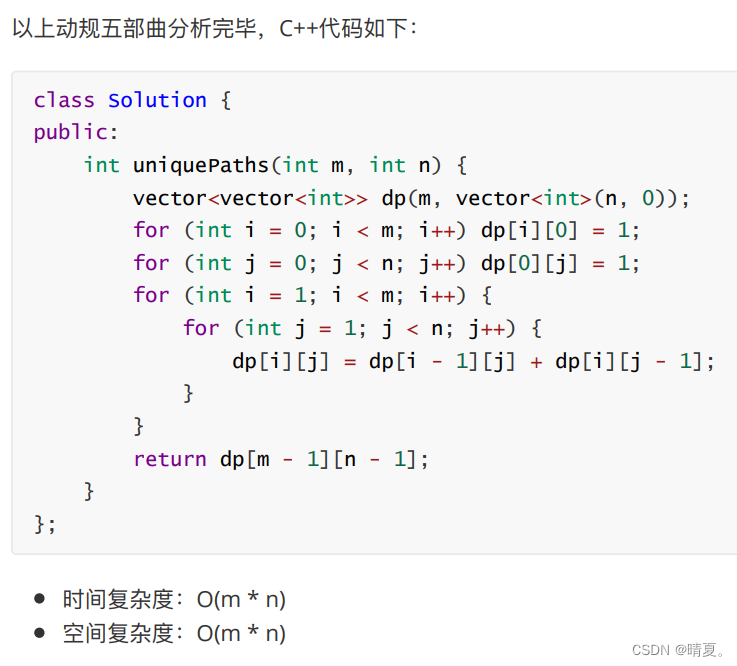
代码如下,很好写:
 ?
?
?
当然,还有数学方法:
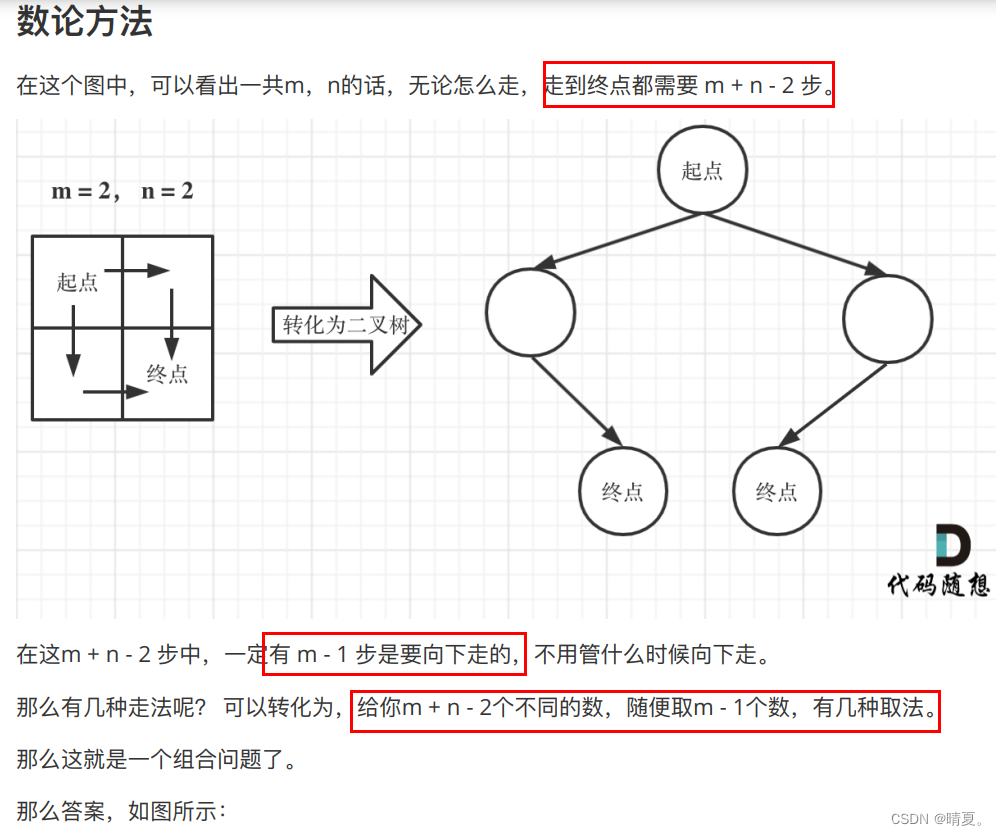
?
 ?
?
?
但是有一点需要注意,阶乘容易溢出!

?
所以正确代码如下:

?
?
不同路径2:

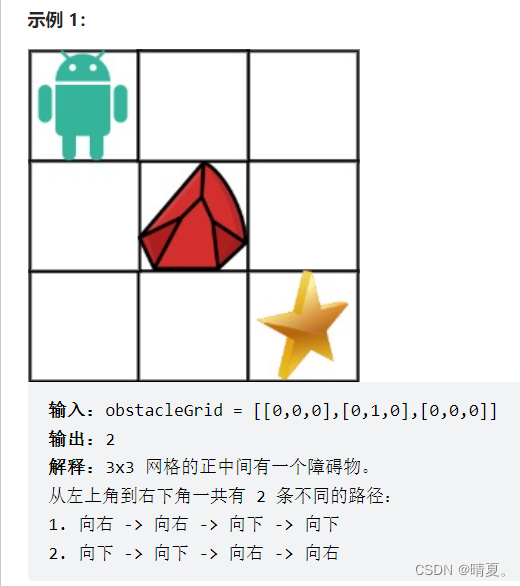
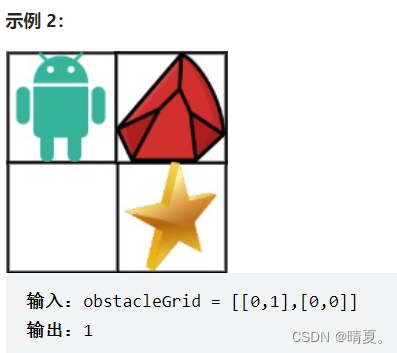
与上文不同,此处多了一个障碍物。
?
?
?和上面那题大体相同,区别在于:

所以代码如下:
 ?
?
整数拆分

?
对于dp[i],其代表的意义是数字为i时,最大的乘积。
而dp[i],对于数字i,其可以由1和i-1,2和i-2,3和i-3……加过来,加到i-1和1。
对于拆分出来的i和j,这个数字所能得到的最大乘积,由于是从前往后遍历,所以可以直接永dp[i-j]和dp[j]得出。
所以dp[i]=max(dp[i],dp[i-j]*dp[j])
不过需要注意一下,此处的dp[i]值,对于i从1到3需要做一下特殊处理。
因为例如dp[3],直接脑算,值应该是2+1=3,然后2x1=2,好像看似dp[3]的值是2。
但是我们在当i大的时候,计算dp[i]值时,需要用到的dp[i-j]和dp[j]时,假如此时i-j或者j为3,那么此时dp[3]不应该是2,而应该是3!
因为此时的3,是i-j或者j得到的结果,是已经拆分过的!所以它代表的乘积就是它本身!而前面计算出的dp[3]为2,是因为单纯计算dp[3]它是需要拆分的,。
对于dp的i值为1~3时,其dp值代表的是已经拆分过的,也就是说不需要再拆分了。
换个角度理解,i为1~3时,不拆分才是最大值!对于i从4开始时,对于4及以后的数字来说,此时拆分才能得到最大值!
所以我们就对1~3特殊处理一下,i从4开始时使用递推公式。
