目录
一,题目描述
英文描述
Given a string s that contains parentheses and letters, remove the minimum number of invalid parentheses to make the input string valid.
Return all the possible results. You may return the answer in any order.
中文描述
给你一个由若干括号和字母组成的字符串?
s?,删除最小数量的无效括号,使得输入的字符串有效。返回所有可能的结果。答案可以按?任意顺序?返回。
示例与说明

来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/remove-invalid-parentheses
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
二,解题思路
参考三叶大佬的思路@宫水三叶【【宫水三叶】将括号的「是否合法」转化为「数学判定」】
目标字符串的形成过程中,对每个字符都有 取 和 不取 两种选择,因此可以考虑dfs递归的方法暴力遍历每种情况。
为方便计算,引入几个变量:
- max记录最多可以匹配的括号对数,max取值为左右括号数目中较小的那个;
- 用score记录左右括号匹配情况,左括号score++,右括号score--。score < 0 表明左括号数目不足以匹配右括号,score > max 表明左括号数目超出可以匹配的最多括号对数;
- lDel和rDel分别记录需要删除的左右括号数目;
- maxLen字符串最大长度 = 原字符串长度 - lDel - rDel;
递归的出口条件:
- 左括号数目不足以匹配右括号数目。score < 0;
- 左括号数目大于可以匹配的最多括号对数(比如左括号有5个,右括号有3个,最多只能匹配3对括号)。score? > max;
- 需要删除的左、右括号数目小于0。lDel < 0 || rDel < 0;
- 已经遍历字符串中所有字符。index = s.length();
当需要删除的左、右括号数目为0,并且当前字符串长度为字符串最大长度maxLen时,将其添加到结果集中即可。
三,AC代码
Java
DFS
class Solution {
int l, r, max, maxLen;// 分别记录左括号数目、右括号数目、最多可以匹配的括号对数、最长子串长度
Set<String> ans = new HashSet<>();
public List<String> removeInvalidParentheses(String s) {
for (int i = 0; i < s.length(); i++) {
if (s.charAt(i) == '(') l++;
else if (s.charAt(i) == ')') r++;
}
max = Math.min(l, r);// 最多可以匹配的括号对数
dfs(0, "", s, 0);
return new ArrayList<String>(ans);
}
// index记录当前遍历的下标、tem为当前形成的字符串、s为原字符串、score为得分(左括号加一分,右括号减一分)
public void dfs(int index, String tem, String s, int score) {
if (score < 0 || score > max) return;
if (index == s.length()) {// !!!遍历完所有字符
if (score == 0 && tem.length() >= maxLen) {
if (tem.length() > maxLen) {
ans.clear();
maxLen = tem.length();
}
ans.add(tem);
}
return;// !!!这里也是出口条件之一
}
char c = s.charAt(index);
if (c == '(') {
dfs(index + 1, tem + '(', s, score + 1);
dfs(index + 1, tem, s, score);
} else if (c == ')') {
dfs(index + 1, tem + ')', s, score - 1);
dfs(index + 1, tem, s, score);
} else {
dfs(index + 1, tem + c, s, score);
}
}
}DFS+剪枝
class Solution {
int max, maxLen;// 分别记录最多可以匹配的括号对数、最长子串长度
Set<String> ans = new HashSet<>();
public List<String> removeInvalidParentheses(String s) {
int l = 0, r = 0;// 记录左右括号数目
int lDel = 0, rDel = 0;// lDel需要删除的左括号数目,rDel需要删除的右括号数目
for (int i = 0; i < s.length(); i++) {
if (s.charAt(i) == '(') {
l++;
lDel++;
}
else if (s.charAt(i) == ')') {
r++;
if (lDel > 0) lDel--;
else rDel++;
}
}
max = Math.min(l, r);// 最多可以匹配的括号对数
maxLen = s.length() - lDel - rDel;// 最长子串长度:总长度-需要删除的左右括号数
dfs(0, "", s, 0, lDel, rDel);
return new ArrayList<String>(ans);
}
// index记录当前遍历的下标、tem为当前形成的字符串、s为原字符串、score为得分(左括号加一分,右括号减一分)、lDel需要删除的左括号数目、rDel需要删除的右括号数目
public void dfs(int index, String tem, String s, int score, int lDel, int rDel) {
if (score < 0 || score > max || lDel < 0 || rDel < 0) return;// 出口:不符合条件
if (lDel == 0 && rDel == 0 && tem.length() == maxLen) {
ans.add(tem);
}
if (index == s.length()) {// !!!遍历完所有字符
return;// !!!这里也是出口条件之一
}
char c = s.charAt(index);
if (c == '(') {
dfs(index + 1, tem + '(', s, score + 1, lDel, rDel);
dfs(index + 1, tem, s, score, lDel - 1, rDel);// 不添加当前字符,需要删除的左括号数目减一
} else if (c == ')') {
dfs(index + 1, tem + ')', s, score - 1, lDel, rDel);
dfs(index + 1, tem, s, score, lDel, rDel - 1);// 不添加当前字符,需要删除的右括号数目减一
} else {
dfs(index + 1, tem + c, s, score, lDel, rDel);
}
}
}四,解题过程
第一搏
一开始想法很简单,先遍历一遍字符串,看看多出来多少个右括号,并记录他们的位置。
以这些位置作为最后要删除的右括号,依次尝试删除之前出现的右括号,并将结果存入set中,举个例子:s = "()())()"
可以看出最晚 i=4 时,必须要删除一个右括号,删除之前的任何一个右括号都可以使得最终的字符串括号有效。
同理,最少需要删除的括号数目就是多出来的右括号数目,而且之前遍历时已经获取了他们最晚删除的位置。
class Solution {
public List<String> removeInvalidParentheses(String s) {
int left = 0;// 记录左括号数目
List<Integer> rightDeletePos = new ArrayList<>();// 记录需要删除的最右侧右括号位置
List<Integer> posToDelete = new ArrayList<>();
Set<String> record = new HashSet<>();// 记录遍历所有的可能解并去重
List<String> ans = new ArrayList<>();
if (s.charAt(0) == ')') return ans;// !!! [")("]
for (int i = 0; i < s.length(); i++) {
char c = s.charAt(i);
if (c == '(') left++;
else if (c == ')') {
if (left > 0) left--;
else rightDeletePos.add(i);
}
}
if (rightDeletePos.size() == 0) return ans;
getAns(record, s, rightDeletePos, posToDelete);
return new ArrayList<String>(record);
}
public void getAns(Set<String> record, String s, List<Integer> rightDeletePos, List<Integer> posToDelete) {
if (rightDeletePos.size() == posToDelete.size()) {
record.add(removeChars(s, posToDelete));
return;
}
for (int pos : rightDeletePos) {
for (int i = 0; i <= pos; i++) {
if (!posToDelete.contains(i) && s.charAt(i) == ')') {
posToDelete.add(i);
getAns(record, s, rightDeletePos, posToDelete);
posToDelete.remove(posToDelete.size() - 1);
}
}
}
}
public String removeChars(String s, List<Integer> posToDelete) {
StringBuilder sb = new StringBuilder(s);
for (int i = 0; i < posToDelete.size(); i++) {
int pos = posToDelete.get(i) - i;// 每次删除字符后,字符串长度减一,对应后面记录的位置需要减一
sb.deleteCharAt(pos);
}
return new String(sb);
}
}心细的同学可能已经发现了,上面的思路中有个非常明显的缺陷:只考虑了右括号数目多于左括号的情况
- 左括号数目大于右括号数目:处理流程和上面的思路类似,不过需要从右向左遍历字符串,记录多出来的左括号数目位置,然后进一步处理;
- 左括号数目等于右括号数目:类似于这样s="))()()((",依次执行上面两种情况的处理方法即可,先删除多余右括号,再删除多余左括号;
以上问题大概就可以解决了(因为没亲手实现出来),可以看出思路勉强还可以,但是实现过程较为复杂和繁琐
第二搏
目标字符串的形成过程中,对每个字符都有 取 和 不取 两种选择,因此可以考虑dfs递归的方法暴力遍历每种情况。
递归的出口条件:
- 1,左括号数目不足以匹配右括号数目;
- 2,左括号数目大于可以匹配的最多括号对数(比如左括号有5个,右括号有3个,最多只能匹配3对括号);
- 3,已经遍历字符串中所有字符;
其中遍历所有字符后,可以对当前形成的字符串进行校验,考虑是否加入结果集(左右括号数目完全匹配)、清空并更新结果集(当前字符串长度大于结果集中字符串长度,需要删除的字符更少,优先选择)
class Solution {
int l, r, max, maxLen;// 分别记录左括号数目、右括号数目、最多可以匹配的括号对数、最长子串长度
Set<String> ans = new HashSet<>();
public List<String> removeInvalidParentheses(String s) {
for (int i = 0; i < s.length(); i++) {
if (s.charAt(i) == '(') l++;
else if (s.charAt(i) == ')') r++;
}
max = Math.min(l, r);// 最多可以匹配的括号对数
dfs(0, "", s, 0);
return new ArrayList<String>(ans);
}
// index记录当前遍历的下标、tem为当前形成的字符串、s为原字符串、score为得分(左括号加一分,右括号减一分)
public void dfs(int index, String tem, String s, int score) {
if (score < 0 || score > max) return;
if (index == s.length()) {// !!!遍历完所有字符
if (score == 0 && tem.length() >= maxLen) {
if (tem.length() > maxLen) {
ans.clear();
maxLen = tem.length();
}
ans.add(tem);
}
return;// !!!这里也是出口条件之一
}
char c = s.charAt(index);
if (c == '(') {
dfs(index + 1, tem + '(', s, score + 1);
dfs(index + 1, tem, s, score);
} else if (c == ')') {
dfs(index + 1, tem + ')', s, score - 1);
dfs(index + 1, tem, s, score);
} else {
dfs(index + 1, tem + c, s, score);
}
}
}
第三搏
在遍历原字符串时,其实可以得到需要删除的左、右括号数目,根据这个条件可以在递归过程中避免部分不必要的递归分支
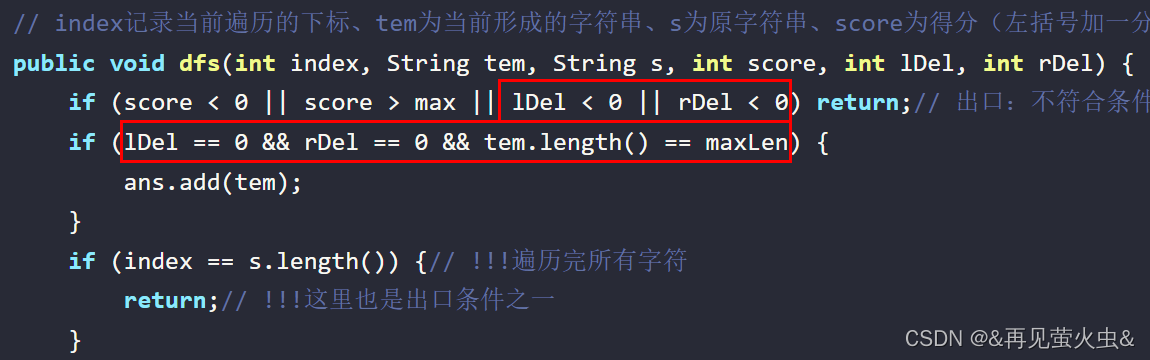

可以看出剪枝的效果非常明显!*★,°*:.☆( ̄▽ ̄)/$:*.°★* 。
