最长上升子序列(一)
牛客链接:NC163 最长上升子序列(一)
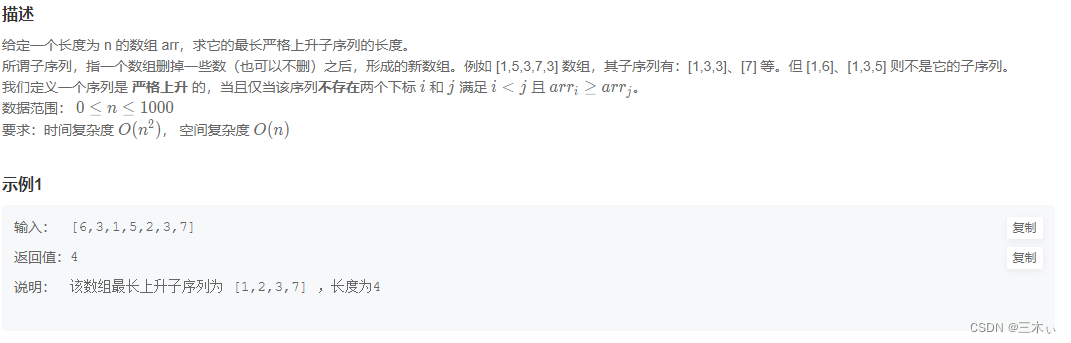
定义长度为n的ans数组,用以保存以arr[i]结尾的最长严格上升子序列的长度。在每次获得最长序列的时候进行比较从而得到最终结果。结果满足复杂度要求。
class Solution {
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
* 给定数组的最长严格上升子序列的长度。
* @param arr int整型vector 给定的数组
* @return int整型
*/
int LIS(vector<int>& arr) {
// write code here
if(arr.size()==0)
return 0;
int res = 0;
vector<int> ans(arr.size(),1);
for(int i = 1; i < arr.size();++i){
for(int j =0; j<i; ++j){
if(arr[i]>arr[j])
{
ans[i] = max(ans[i],ans[j]+1);
}
}
res = max(ans[i] ,res);
}
return res;
}
};
最长上升子序列(二)
牛客链接:NC164 最长上升子序列(二)
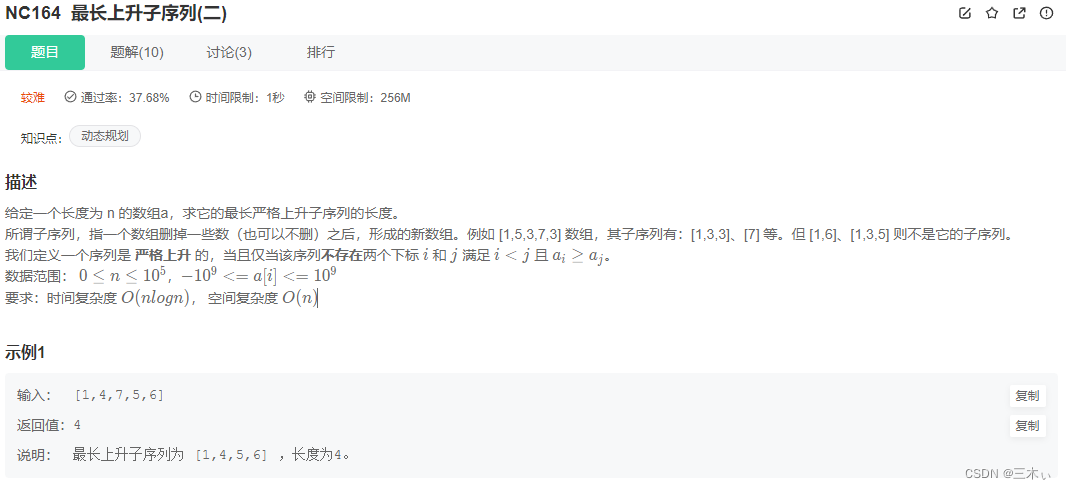
和上题目目的相同,只是更严格的要求了时间和空间复杂度。这里使用动态规划+二分的思路。
arr[i]用来存储尽可能小的值,因为小的值在后续中,更可能寻找到大的值从而使得长度增加。
遍历每个a[ i ],如果严格大于arr的最后一个数,则加入arr;
否则,找到找到大于等于他的最小的一个数,进行替换。
最终获得的arr的长度就是答案。
//实现1:手写二分
class Solution {
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
* 该数组最长严格上升子序列的长度
* @param a int整型vector 给定的数组
* @return int整型
*/
int LIS(vector<int>& a) {
// write code here
int n=a.size();
if(n==0)
return 0;
vector<int> arr;
arr.push_back(a[0]);
for(int i =1;i<n;++i){
if(a[i]>arr.back()){
arr.push_back(a[i]);
}
else{
int l=0, r = arr.size()-1,mid;
while(l<r){ //寻找>=的位置 也可以直接使用lower_bound() 替代
mid = (l+r)>>1;
if(arr[mid]>=a[i])
r = mid;
else
l = mid+1;
}
arr[l] = a[i]; //更新长度为l的子序列的最小值
}
}
return arr.size();
}
};
//实现2:调用函数
class Solution {
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
* 该数组最长严格上升子序列的长度
* @param a int整型vector 给定的数组
* @return int整型
*/
int LIS(vector<int>& a) {
// write code here
vector<int> arr;
for(int i : a){
vector<int>::iterator it = lower_bound(arr.begin(),arr.end(),i);
if(it == arr.end())
arr.push_back(i);
else
*it = i;
}
return arr.size();
}
};
最长公共子序列(一)
牛客链接:NC165 最长公共子序列(一)

题解一:满足要求1
定义ans[][]二维数组,其中ans[i][j] 表示s1中第i个字符和s2中第j个字符为结尾的最长公共子序列。如果 s1[i-1]==s2[j-1],结果则为ans[i-1][j-1]+1,否则最大值在ans[i-1][j], ans[i][j-1]中产生。
class Solution {
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
* s1和s2最长公共子序列的长度
* @param s1 string字符串
* @param s2 string字符串
* @return int整型
*/
int LCS(string s1, string s2) {
// write code here
vector<vector<int>> ans(s1.size()+1,vector<int>(s2.size()+1,0));
for(int i = 1;i<=s1.size();++i)
for(int j = 1; j<=s2.size(); ++j)
{
if(s1[i-1] == s2[j-1])
ans[i][j] = ans[i-1][j-1] + 1;
else
ans[i][j] = max(ans[i-1][j], ans[i][j-1]);
}
return ans[s1.size()][s2.size()];
}
};
解法2:进阶版
解法1中,建立的arr数组,其实每次都只是用了当前行和之前一行的数据,因此可以使用两个一维数组代替。
b数组用于保存上次的结果,a数组用于计算当前行的结果。
class Solution {
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
* s1和s2最长公共子序列的长度
* @param s1 string字符串
* @param s2 string字符串
* @return int整型
*/
int LCS(string s1, string s2) {
// write code here
int n = min(s1.size(),s2.size());
vector<int> a(n+1,0);
vector<int> b(n+1,0);
if(s1.size()<s2.size())
swap(s1,s2);
for(int i = 1; i<=s1.size();++i){
for(int j = 1; j<=s2.size(); ++j)
{
if(s1[i-1] == s2[j-1])
a[j] = b[j-1] + 1;
else
a[j] = max(a[j-1],b[j]);
}
swap(a, b); //交换a,b
a = vector<int>(n+1,0); //初始化a为全0的数组
}
return b[n];
}
};
