题目

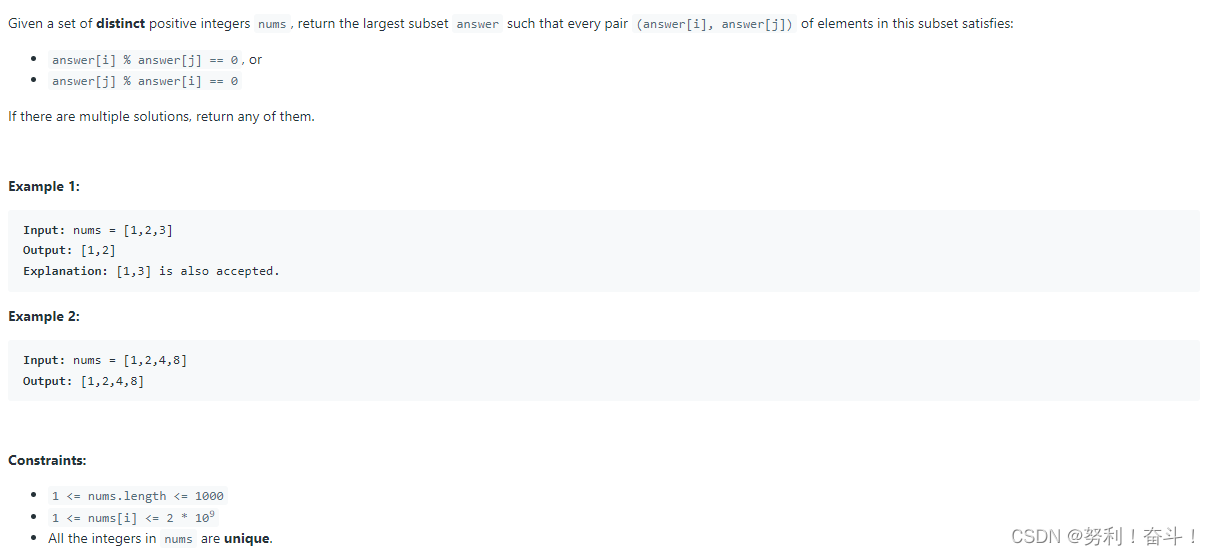
在这里插入图片描述

解法：dp

这道题目的关键在于想到一个subset在符合条件的情况下，如果另一个数字能够整除这个subset中最大的数字，证明这个数字能够被扩展到这个subset中，那么这就是一种子问题关系

将数组排序，保证在数字的某个位置，当前数字的所有因数或者能整除的数都在这个数前面，这样我们才能用上面提到的子问题关系
dp状态转移方程：dp[i] = max(dp[j] + 1 for j < i and nums[i]%nums[j]==0)
同时由于需要返回最终的subset而不是长度，这边需要用到一个技巧，构建一个同等长度数组pre，这个数组i位置储存的是i位置的数字之前的那个数，这个之前的关系在哪边更新需要注意
dp的同时用一个变量keep track那个最优subset中最大的数字，避免重复遍历
利用pre数字形成最终答案

class Solution {
public:
    vector<int> largestDivisibleSubset(vector<int>& nums) {
        // sort the nums so that every number's divisible element number is before this number
        // only that we can use dp
        sort(nums.begin(),nums.end());
        // dp[i] means the larest length of subset that can be formed using nums[i] as the largest number
        vector<int> dp(nums.size(),1);
        // since we need the subset it self rather than the length of the subset, we need an array to keep track the previous element in the largest subset
        // pre[a] = b, meaning the previous number before number at posistion a is at position b
        vector<int> pre(nums.size(),-1);
        int max_ = 0;
        int max_index = 0;
        for(int i=1;i<nums.size();i++){
            for(int j = i-1;j>=0;j--){
                if(nums[i]%nums[j] == 0){
                    if(dp[j]+1 > dp[i]){
                        pre[i] = j;
                        dp[i] = dp[j] + 1;
                    }
                }
            }
            // we also need to keep track of the position where the answer occur
            if(dp[i] > max_){
                max_ = dp[i];
                max_index = i;
            }
        }
        vector<int> ans;
        while(max_index >= 0){
            ans.push_back(nums[max_index]);
            max_index = pre[max_index];
        }
        return ans;
    }
};