在数据结构中比较熟知的最小生成树的几种算法,知道可以这样去做,但是正确性却没有特别强调,也没有重点验证,下面从理论证明最小生成树的几种算法还有它们正确性的验证。
文章目录
一、概念
对一个带权重的无向连通图,有权重以后生成树的所有的权才有大小,如果权重都为1的话那就没有必要去比较了。
生成树的概念是首先有一个图,从图里面要找到一颗树来,这个树要包含所有顶点,树是连通的,从图里找出一些边来构造这个树,这个树的选择就有很多种,要包含这些点的路径就有很多种,但是其中有一个是最小的,比较的是最小的生成树的权重,所最小的生成树的权重如果能达到最小,那就是最小生成树。
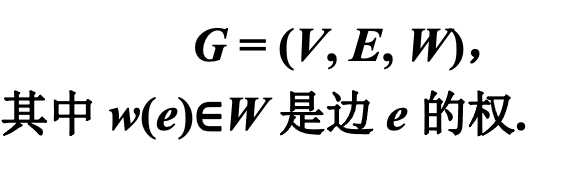
G 的一棵生成树T 是包含了G 的所有顶点的树, 树中各边的权之和W(T) 称为树的权,具有最小权的生成树称为G 的最小生成树.
二、实例
1、图示
G=(V,E,W),V={1,2,3,4,5,6},W 如图所示.
E = {{1,2},{1,3},{1,4},{2,3},{2,5},{3,4},{3,5},{3,6},{4,6},{5,6}}
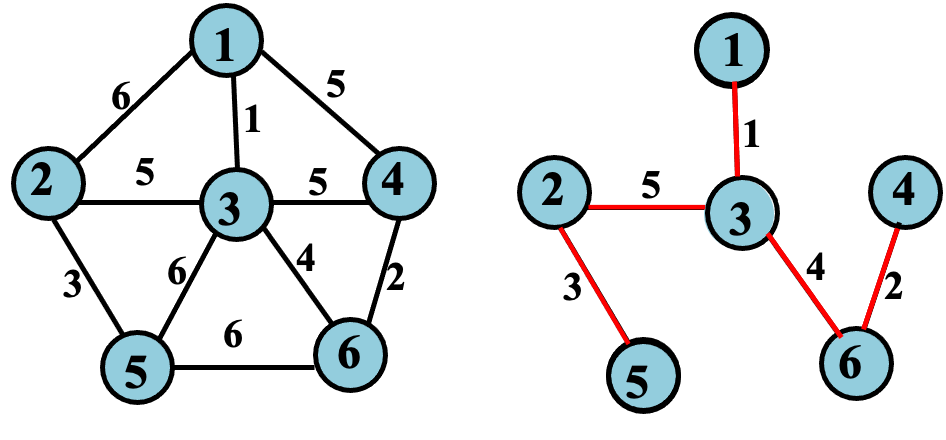
左边是一个图,图里面连接的权重有顶点:1,2,3,4,5,6。顶点1与它相临的顶点有顶点2、3、4。顶点3相邻的顶点1、2、4、5、6……权重都在边上。
2、构造最小生成树
(1)从顶点1出发,权值最小的边是1,所以到达顶点3
(2)从顶点3出发,权值最小的边是4,所以到达顶点6
(3)从顶点6出发,权值最小的边是2,所以到达顶点4
(4)从顶点4出发,任意一条边都会构成回路,退回顶点6
(5)从顶点6出发,任意一条边都会构成回路,退回顶点3
(6)从顶点3出发,除权值为4外权值最小的为5,到达顶点2
(7)从顶点2出发,权值最小的边是3,所以到达顶点5
右边这颗树包含了所有顶点,这颗树里面有很多边,这些边的所有的权重加起来是最小的,其实它的构造过程就是由这些边来构成的,这些生成树由这些性质
三、性质
如果是生成树,这个树是没有环的,只有n-1条边,所有的顶点数是n,图G是n个顶点,接下来连接所有顶点。找到任何一颗生成树,如果在加入任何一条不在这颗树上的任意一条边,那么都会形成一个圈。
1、命题 设G是n 阶连通图
那么
(1) T 是G 的生成树当且仅当T 无圈且有n-1条边.
(2) 如果T 是G 的生成树,e?T,那么T∪{ e }含有一个圈C(回路).
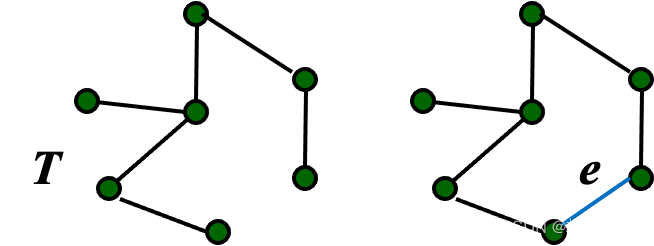
把不在这个树以外的任何一条边加进来就形成圈了,在这个圈里面可以去掉任何一条边,由一颗生成树变化成另外一个生成树,这两个生成树之间有不同,所有点都在里面不同就只能在边上不同,另外一个不同就是生成树的权重(所有边之和)
(3) 去掉圈C的任意一条边,就得到G的另外一棵生成树T’
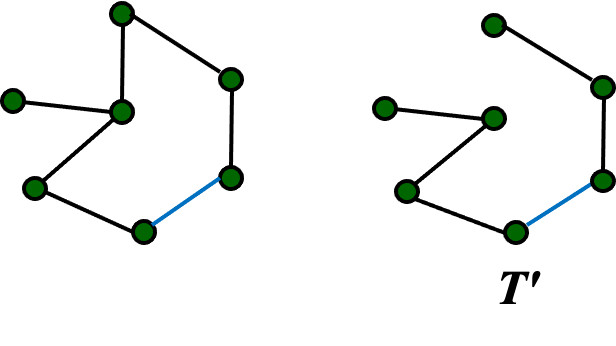
这些性质在证明Prim算法和Kruskal算法会在证明的时候用到
四、生成树性质的应用
如果能够改进生成树的性质,加上一条本来不在这个树里面的边,因为加进去之后形成回路,去掉一条边得到一个新的树。如果这个树的权重有降低的话,那就找到了一个更好的生成树。
1、算法步骤
选择边.
约束条件:不形成回路
截止条件:边数达到n-1.
2、改进生成树T 的方法
在T 中加一条非树边e , 形成回路
C,在C 中去掉一条树边ei,形成一棵新的生成树T’
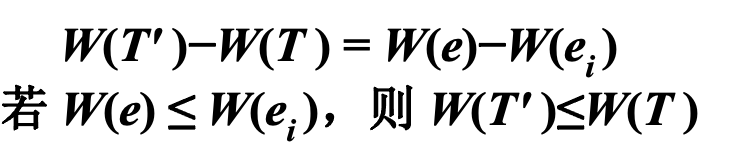
五、求最小生成树
1、问题:
给定连通带权图G = (V, E, W),w(e)∈W是边e 的权。求G 的一棵最小生成树。
在无向连接带权图里面,如何寻找一颗最小生成树,就是我们熟悉的Prim算法和Kruskal算法。
2、贪心法:
Prim 算法,Kruskal算法
生成树在网络中有着重要的应用,网络传输的时候有很多数据要从一个地方发到另外一个地方去,当这个网络拓扑是确定的情况下,知道传输代价的时候,怎么样让传输代价达到最小,那么数据的跳转,整个拓扑里找到通路。
