一、问题提出:
// 算法要求:请编写?个算法,能够确定?个切割方案,使切割的总代价最?。?
void MinCost(int L,int n,int *p){
//调用函数输出一个切割最小的代价和,结果通过cout输出,均为int类型
}
//你的代码只需要补全上方函数来实现算法,可根据自己需要建立别的函数
//其中L是钢条长度,n是位置点个数,p包含n 个切割点的位置(乱序)
//只需要提交这几行代码,其他的都是后台系统自动完成的。
二、代码实现:
其实质就是钢条切割的问题,是一个十分常见的问题,在这里就不过多赘述。直接上代码。
void MinCost(int L,int n,int *p)
{
void lowestCost(int m, int n, int* &x, int xlen, int** &memo);
int** memo;//备忘录矩阵
int INF=100000000;
int xlen = n + 2;//在输入的切割点的基础上考虑最开始和最末端的点
//对切割点位置进行排序
sort(p, p + xlen);
//初始化备忘录
memo = new int*[xlen];
for (int i = 0; i < xlen; i++)
memo[i] = new int[xlen];
for (int i = 0; i < xlen; i++)
{
for (int j = 0; j < xlen; j++)
memo[i][j] = INF;
}
int m=0;
for (int i = 0; i < xlen; i++)
{
memo[i][i] = 0;
if (i + 1 < xlen)
{
memo[i][i+1] = 0;//
}
if (i + 2 < xlen)
{
memo[i][i+2] = p[i + 2] - p[i];//
}
}
int temp;
//应采用步长
for (int step = 3; step <= p[xlen - 1]; step++)//注意边界
{
for (int m = 0; m < xlen; m++)
{
if (m + step <= xlen - 1)
{
for (int i = m + 1; i < m + step; i++)
{
temp = memo[m][i] + memo[i][m + step] + p[m + step] - p[m];
if (temp < memo[m][m + step])
{
memo[m][m + step] = temp;
}
}
}
}
}
cout<<memo[m][xlen - 1]<<endl;
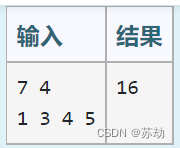
}三、测试用例: