个人学习 代码随想录 的做题笔记,如果对你有帮助,请一键三连(点赞+收藏+关注)哦~ 感谢支持!欢迎各位在评论区与博主友好讨论!缓慢更新中……
一般从以下几点分别考虑:
- 子状态:
- 递推状态:
- 初始值:
- 遍历顺序:
- 返回结果:
1.斐波那契数列:
0,1,1,2,3……
求前两个数之和可得此数列。
- 子状态:F(n)
- 递推状态:F(n)=F(n-1)+F(n-2)
- 初始值:F(0)=0,F(1)=F(2)=1
- 遍历顺序:一维数组从左到右
- 返回结果:F(N)
public class Solution {
??public int Fibonacci(int n) {
????// 初始值
????if(n <= 0)
??????return 0;
????int[] a = new int[n + 1];
????a[0] = 0;
????a[1] = 1;
????for(int i = 2; i <= n; ++i)
???{
??????// F(n)=F(n-1)+F(n-2)
??????a[i] = a[i - 1] + a[i - 2];
???}
????return a[n];
?}
}实际上实现这个数列用a,b,result三个值就可以了。
比如:
int a = 1;
int b = 1;
int result = 0;
for (int i = 3; i <= n; i++)//0,1,1
{
????// F(n)=F(n-1)+F(n-2)
result = a + b;
????// 更新值
a = b;
b = result;
}2.最小路径和:
依题意,到F(i,j)能从上面或左面,需要前面的值才能得出接下来的值,建立二维数组存储对应格子的最短路径和?
- 子状态:从(0,0)到达(1,0),(1,1),(2,1),...(m-1,n-1)的最短路径。F(i, j): 从(0,0)到达F(i, j)的最短路径
- 递推状态:F(i,j)=F(i-1, j)+F(i, j-1)
- 初始值:F(0, j)=1,F(i, 0)=1? ?即最左边一列到其他列只能往右,最上边一行到其他行只能往下
- 遍历顺序:从左到右按顺序即可
- 返回结果:F(m-1,n-1)
class Solution {
public:
int minPathSum(vector<vector<int> >& grid) {
// write code here
if(grid.size()==0)
return 0;
int m=grid.size();
int n=grid[0].size();
for(int i=1;i<m;i++)
grid[i][0]=grid[i-1][0]+grid[i][0];
for(int j=1;j<n;j++)
grid[0][j]=grid[0][j-1]+grid[0][j];
for(int i=1;i<m;i++)
{
for(int j=1;j<n;j++)
{
grid[i][j]=min(grid[i-1][j],grid[i][j-1])+grid[i][j];
}
}
return grid[m-1][n-1];
}
};有障碍版本:
自己写的繁琐:?
class Solution {
public:
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
if(obstacleGrid[obstacleGrid.size()-1][obstacleGrid[0].size()-1]==1)
return 0;
vector<vector<int>>a(obstacleGrid.size(),vector<int>(obstacleGrid[0].size(),0));
for(int i=0;i<obstacleGrid.size()&&obstacleGrid[i][0]==0;i++)
{
a[i][0]=1;
}
for(int i=0;i<obstacleGrid[0].size()&&obstacleGrid[0][i]==0;i++)
{
a[0][i]=1;
}
for(int i=1;i<obstacleGrid.size();i++)
{
for(int j=1;j<obstacleGrid[0].size();j++)
{
if(obstacleGrid[i-1][j]==0&&obstacleGrid[i][j-1]==0)
{
a[i][j]=a[i-1][j]+a[i][j-1];
}
else if(obstacleGrid[i-1][j]==0&&obstacleGrid[i][j-1]==1)
a[i][j]=a[i-1][j];
else if(obstacleGrid[i][j-1]==0&&obstacleGrid[i-1][j]==1)
a[i][j]=a[i][j-1];
}
}
return a[obstacleGrid.size()-1][obstacleGrid[0].size()-1];
}
};大佬写的:?
class Solution {
public:
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
int m = obstacleGrid.size();
int n = obstacleGrid[0].size();
vector<vector<int>> dp(m, vector<int>(n, 0));
for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++)
dp[i][0] = 1;
for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++)
dp[0][j] = 1;
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
if (obstacleGrid[i][j] == 1)
continue;
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
}
};?for循环跳出,进行下一次循环的条件:
if (obstacleGrid[i][j] == 1) continue;
即如果当前格子有障碍,就不算谁能到达它了,此障碍需要被略过。?
3.爬楼梯问题
使用最小花费爬楼梯,带权值楼梯。
依旧是从前一个台阶或前两个台阶可以到达当前台阶。
- 子状态:F(i),到达第?i阶需要的最小体力,c(i)原题给的台阶对应体力
- 递推状态:F(i)=min(F(i-1)+F(i-2))+c(i)
- 初始值:F(1)=c(1),F(0)=c(0),
- 遍历顺序:一维数组从左到右
- 返回结果:由于题意是遍历完体力楼梯数组后还要再上一个台阶,此时对于楼顶来说是不花体力的,但要从前一个台阶和前两个台阶中选出体力最小的。
min(F[c.size() - 1], F[c.size() - 2]);
4.?整数拆分
- 子状态:F(i),数字i拆分后对应的最大的乘积
- 递推状态:F(i)=max(F[i],max(j*(i-j),F[i-j]*j));?max(上一次计算的乘积,拆分成两个数,拆分成多个数)
- 初始值:F(2)=1; 题意n从2开始
- 遍历顺序:一维数组从左到右,i=3,j=1; F(2)已经初始化了,第一次循环计算i-j刚好可得2
- 返回结果:F(n);
class Solution {
public:
int integerBreak(int n) {
vector<int>a(n+1);
a[2]=1;
for(int i=3;i<=n;i++)
{
for(int j=1;j<i-1;j++)
{
a[i]=max(a[i],max(j*(i-j),a[i-j]*j));
}
}
return a[n];
}
};5.不同的二叉搜索树
1个节点:1个二叉树
2个节点:2个二叉树
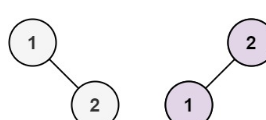
3个节点:5?个二叉树
?
可以发现:
1为头结点:2个右子树的布局与2个节点时相同;
2为头结点:左子树和右子树与1个节点时相同;
3为头结点:2个左子树的布局与2个节点时相同
此时便可想到一种递推关系:
F(1)=1,
F(2)=F(1)*F(0)+F(1)*F(0)=2,?即左子树为1节点*右子树0个节点的树的个数+左子树为0节点*右子树1个节点的树的个数
F(3)=F[2] * F[0] + F[1] * F[1] + F[0] * F[2]=2*1+1*1+1*2=5
模拟一下该过程可得递推公式,i,j的范围
- 子状态:F(i),i个节点对应的二叉树个数
- 递推状态:F(i)+=F(i-j)*F(j-1);
F[i] += F[以j为头结点左子树节点数] * F[以j为头结点右子树节点数]
j相当于是头结点的元素,从1遍历到i为止。j<=i
递推公式:F(i)+=F(i-j)*F(j-1),j-1 :j为头结点左子树节点数量,i-j :以j为头结点右子树节点数量
- 初始值:F(0)=1,乘法计算
- 遍历顺序:一维数组从左到右
- 返回结果:F(n);
class Solution {
public:
int numTrees(int n) {
vector<int>a(n+1);
a[0]=1;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=i;j++)
{
a[i]+=a[j-1]*a[i-j];
}
}
return a[n];
}
};?背包问题:
背包:最大容量;物品:价值、体积、每个物品的数量
01背包:每个物品的数量只有一个,放一个或者不放入背包
完全背包:每个物品的数量有无数个,放几个或者不放入背包
二维数组的01背包:
n 个物品和一个大小为 m 的背包. 给定数组 W表示每个物品的大小和数组 V 表示每个物品的
价值
??
1.子状态:f[i][j]:前i个物品放入大小为j的背包中所获得的最大价值
2.递推状态:装不下和装得下时放还是不放:
①背包容量不够不能放入第i号物品,f[i-1][j];?
②背包容量够可以放入第i号物品,包括两种状态:放进去或者不放进去,选择一种最终价值最大的。
f[i-1][j]:不放;
f[i - 1][j - W[i]] + V[i]:先为第i号物品腾出空间,即减去该物品的容量后包内还剩多少容量,再加上i号物品的价值。
f[i][j]=max(f[i-1][j], f[i - 1][j - W[i]]? + V[i])。
3.初始值:f[i][0]=0:0~i个物品,背包容量为0时,一个物品都放不进去,价值仍为0。
f[0][j]=0:没放物品价值也为0
4.遍历顺序:双重循环,先遍历谁都行。从递推公式可得f[i][j]由(i-1,j),和(i-1,j - W[i])得到的。在左上角方向(包括正上方向)。
5.返回结果:f(N-1,m);
//动态规划部分代码实现
for (int i = 1; i < N; ++i)
{
for (int j = 1; j != M; ++j)
{
if (A[i - 1] > j)
{
result[i][j] = result[i - 1][j];
}
else
{
int newValue = result[i - 1][j - A[i - 1]] + V[i - 1];
result[i][j] = max(newValue, result[i - 1][j]);
}
}
}一维数组01背包:
上面的算法在计算第i行元素时,只用到第i-1行的元素,所以二维的空间可以优化为一维空间。
但是如果是一维向量,需要从后向前计算,因为后面的元素更新需要依靠前面的元素未更新的值。
1.子状态:f[j]:大小为j的背包中所获得的最大价值
2.递推状态:装不下和装得下时放还是不放:
①背包容量不够不能放入第i号物品,f[[j];?
②背包容量够可以放入第i号物品,包括两种状态:放进去或者不放进去,选择一种最终价值最大的。
f[j]:不放,容量不变;
f[ j - W[i] ] + V[i]:先为第i号物品腾出空间,即减去该物品的容量后包内还剩多少容量,再加上i号物品的价值。
f[ j ]=max( f[ j ], f[ j - W[ i ] ] + V[ i ])。
3.初始值:都初始为0
f[0][j]=0:没放物品价值也为0
4.遍历顺序:双重循环,只能先遍历物品再遍历背包容量,因为如果先遍历背包,就是在当前容量中,现有物品中选出价值最大一个的放入。倒叙遍历是保证物品i只被放入一次。如果正序遍历物品 i 就会被重复加入多次。
二维数组正序遍历是因为f[ i ][ j ]通过上一层f[i - 1][j]计算而来,本层的f[ i ][ j ]不会被覆盖。
5.返回结果:f(m);
class Solution {
public:
int backPackII(int m, vector<int> A, vector<int> V) {
if (A.empty() || V.empty() || m < 1)
{
return 0;
}
???
????const int N = A.size();
const int M = m + 1;
vector<int> result;
result.resize(M, 0);
for (int i = 0; i != N; ++i)
{
for (int j = M - 1; j > 0; --j)
{
if (A[i] > j)
{
result[j] = result[j];
}
else
{
int newValue = result[j - A[i]] + V[i];
result[j] = max(newValue, result[j]);
}
}
}
return result[m];
}
};6.分割等和子集
每一个数字只能选一次,有最大和的限制-->01背包存在。分割成两个子集,和相等。那直接找和为sum/2的子集就行了。
- 子状态:a[j],容量为 j 时的最大和
- 递推状态:a[j]=max(a[j],a[j-nums[i]]+nums[i]);
- 初始值:都为0
- 遍历顺序:逆序遍历 j,再写一遍原因:此递推公式与二维数组的递推公式意义一样,a[j]对应a[i-1][j],a[j-nums[i]] +nums[i]对应a[i-1][j-nums[i]] +nums[i]。逆序遍历,a[j-nums[i]]使用的是上一行(逻辑上)的值。正序遍历,a[j-nums[i]]就会被更新,接下来的a[j]使用的就不是原来的值了,应该让a[j]从未更新的值里选出最大的。
a[j] (新)= a[j] (旧) || a[j - nums[i]] (旧)
- 返回结果:f(sum/2)==sum/2时;
7.最后一块石头的重量
背包最值:每次选2个石头,最终让差值最小。那么把石头分为两堆,每堆石头都选接近(所有石头总重量/2)。把所有石头放进容量为sum/2的背包,求放进去的石头的最大重量x。差值就是sum-2x。
8.目标和
背包组合:要求装满背包容量有几种方法。数组和sum,要被加的数字之和a,要被减的数字(正数)之和b,题目求的目标和 t。
a+b=sum,a-b=t。两式联立求得a=(sum+t)/2,由此可知sum+t为偶数,a也为偶数。
- 子状态:dp[j],装满容量j的方法
- 递推状态:dp[j]=dp[j]+dp[j-nums[i]]:?不选nums[i]+选nums[i]
- 初始值:dp[0]=1,即0容量时有一种方法,就是选0件物品
- 遍历顺序:内部逆序遍历
- 返回结果:dp[a]
9.一和零
dp[i][j],i个0和j个1时对应的最多子集。
递推:可以从放入当前子集,或者不放入,选出最大的。dp[i][j]不放入,dp[i-zero][j-one]+1在 放入后还应该有的0,1的个数对应的子集数的基础上+1。
三维数组表示:
dp[k][i][j] 表示在前 i个字符串中,使用 i 个 0 和 j 个 1 的情况下最多可以得到的字符串数量。
那去掉一个维度,最外层遍历的就是strs中k个字符串。每个字符串统计0,1个数,遍历物品。内层遍历背包容量i,j,倒序遍历。
10.零钱兑换II
看了题解中有说本题像?爬楼梯 这个题。爬楼梯扩充成每次可走1,2……m阶台阶,到达n级台阶有几种方法,是个排列问题。
每种钱可以用无数次,最终和为已给容量大小。题目给出的样例是组合而不是排列,意为 2+2+1与1+2+2是相同的。外部物品,内部背包,且物品的顺序是不变的。
物品无限次选取,而01背包只能选一次物品,保证下标j之前的dp[j]都是经过计算的就行。
- 子状态:dp[j],必须选取conis[i]时,装满容量 j 的方法。
- 递推状态:dp[j]=dp[j]+dp[j-coins[i]]。不用当前物品+用当前物品
- 初始值:dp[0]=1,即0容量时有一种方法,就是选0件物品。
- 遍历顺序:组合问题,外部物品,内部背包,从小到大遍历。
- 返回结果:dp[amount]
11.组合总和
物品无限,有确定的总和即容量,求排列数,完全背包。按排列计算,不同的排列方式就是不同的方法。
- 子状态:dp[j],装满容量 j 的方法。
- 递推状态:dp[j]=dp[j]+dp[j-nums[i]]。不用当前物品+用当前物品
- 初始值:dp[0]=1,无意义,只是为了累加时能计算。
- 遍历顺序:排列问题,外背包,内物品(记得判断条件[j-nums[i]]),从小到大遍历。
- 返回结果:dp[target]
12.零钱兑换?
每种硬币的数量是无限的,凑成总金额所需的?最少的硬币个数?:典型完全背包问题。样例显示不强调组合还是排列,硬币有顺序和没有顺序都不影响硬币的最小个数,for循环内外可交换。
- 子状态:dp[j],装满容量 j 的最小数量。
- 递推状态:dp[j]=min(dp[j],dp[j-coins[i]]+1)。不用当前物品+用当前物品且数量+1
- 初始值:dp[0]=0,凑够0元时,需要0个硬币。剩下的初始化为INT_MAX
- 遍历顺序:都行,内循环是正序。可以判断?if?(a[j?-?coins[i]]?!=?INT_MAX)时,再计算数量。
- 返回结果:dp[amount]
13.完全平方数
乍一看,看不出来什么。模拟一遍过程,就看出来是零钱兑换的相似问题了。
注意以下几点:
1.dp[0]=0。为了能进循环并赋值后面的数,实际无意义。除此之外都初始化为INT_MAX,因为求的是最小值
?2.物品遍历,本来想的是再建一个物品数组,看了答案才知道可以直接dp[j-i*i].
3.先遍历背包:i从1开始,因为完全平方数从1开始
for(int j=0;j<=n;j++)
{
for(int i=1;i*i<=j;i++)
{
a[j]=min(a[j],a[j-i*i]+1);
}
}先遍历物品:
for (int i = 1; i * i <= n; i++)
{
for (int j = 1; j <= n; j++)
{
if (j - i * i >= 0) //判断是否越界
{
dp[j] = min(dp[j - i * i] + 1, dp[j]);
}
}
}14.单词拆分
?字符串是背包,字典是物品。字典里的单词可以无限取出放入背包内。
- 子状态:dp[j],长度为j的字符串是否可以被拆分
- 递推状态:i<j,dp[i]&&[i,j] 这个区间的子串出现在字典里?。那么dp[j]就是true。
- 初始值:dp[0]=true,如果设为false,那么循环结果始终为false
- 遍历顺序:有的题解说都行但建议用外层背包,有的说只能用外层背包。
- 返回结果:dp[s.size()]
?背包做了这些题,稍微一变是不是感觉自己就不会了呢?

15.打家劫舍
通过前面的计算后面的值,该类题也是典型动态规划问题。
- 子状态:dp[i],前i间房可得的最大钱数
- 递推状态:
dp[i]:此时两种可能,第i间房被偷了,第i-1号房子就不能偷,dp[i]=dp[i-2]+nums[i];
没偷第i间,第i-1间就能偷,但可以不偷,反正等于前 i-1个房子的最高金额,dp[i]=dp[i-1];
如果在前i-1间时,第i-1间一定被偷了吗?
假设第i-1间没被偷,dp[i-1]=dp[i-2],则第i间可以被偷:
dp[i]=dp[i-1]+num[i]=dp[i-2]+nums[i]。
第i-1间被偷了,那第i间就不能被偷。
所以,dp[i]=max(dp[i]=dp[i-2]+nums[i],dp[i-1])
3.初始值:dp[0]=nums[0],dp[1]=max(nums[0],nums[1])
4.遍历顺序:?从前到后
5.返回结果:dp[nums.size()-1]
16.打家劫舍II
本题可以转为两个子问题。
从下标0号开始考虑,到倒数第二个,即不选最后一个。
从下标1号到最后一个,即不选第一个。
也可以第一个和最后一个都不选,但这种情况包含在上述两种中了,即他们中不一定非选第一个或是最后一个,具体情况具体分析。
分别求他俩的最大值(和上面的题思路一样,不过是取值范围不同),再算他俩谁大。
17.打家劫舍III
只想到了后序遍历……?
当前节点被偷,它的子节点不能偷,子节点的子节点可以考虑。不偷当前节点,可以偷它的子节点。子节点的子节点的子节点……递归!
不由得想到三种遍历方法,要分别在左子树,右子树找大的。因为通过递归函数的返回值来做下一步计算。
定义一个数组a,下标0表示不偷,下标1为偷。
如果当前为空就返回{0,0}。
递归遍历左子树,右子树。
单层遍历:当前节点被偷,它的子节点不能偷。不偷当前节点,可以选最大子节点(子节点的子节点)偷。
最终返回{单层遍历的两个值}
18.买卖股票的最佳时机
暴力解非常明显的超时了……
- 子状态:dp[i][0],第i天拥有股票时现金的最大金额,dp[i][1],第i天没有股票时现金的最大金额
- 递推状态:
dp[i][0]:
前一天就有股票dp[i-1][0],第i天新买的股票 -prices[i]
dp[i][1]:
前一天没有股票dp[i-1][1],第i天把股票卖出去了dp[i-1][0]+prices[i]
dp[i][0] = max(dp[i - 1][0], -prices[i]);
dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]);
3.初始值:dp[0][0]-=prices[0]:第一天先买股票,dp[0][1]=0:没有股票
4.遍历顺序:?从前到后
5.返回结果:dp[prices.size()-1]
19.买卖股票的最佳时机II
可以多次买卖,那么第i天新买的股票就可能是从前几天没有股票时获得的利润里扣钱,即使最终结果是负值也是正常的。
dp[i][0]:
前一天就有股票dp[i-1][0],第i天新买的股票?dp[i-1][1]-prices[i],唯一与上题不同的地方。
dp[i][0] = max(dp[i - 1][0], dp[i-1][1]-prices[i]);
?20.买卖股票的最佳时机III
仅限两笔买卖,一共五种状态。
0:无操作
1:第一次买入
2:第一次卖出
3:第二次买入
4:第二次卖出
?
1.子状态:dp[i][0],第i天拥有股票时现金的最大金额,dp[i][1],第i天没有股票时现金的最大金额
2.?递推状态:
dp[i][0]:
前一天对股票就没操作dp[i-1][0]
dp[i][1]:
前一天没有股票dp[i-1][1],第i天把股票买了dp[i-1][0]-prices[i]
dp[i][2]:
前一天有股票dp[i-1][2],第i天把股票卖出去了dp[i-1][1]+prices[i]
……
dp[i][0] = dp[i - 1][0];
dp[i][1] = max(dp[i - 1][1], prices[i] -?dp[i - 1][0]);? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? dp[i][2]=max(dp[i-1][2],dp[i-1][1]+prices[i]);? ?
……? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
3.初始值:dp[0][0]=0:dp[0][1]-=prices[0],dp[0][3]-=prices[0]
买入,现金就减少。卖出,现金增加,并且最终取的是最大值,收获利润小于0也没必要计算。
4.遍历顺序:?从前到后
5.返回结果:dp[prices.size()-1][4],因为最后一次卖出的价格一定比第一次卖的贵
21.买卖股票的最佳时机III
?通过上题找规律。
0:无操作
1:第一次买入
2:第一次卖出
3:第二次买入
4:第二次卖出
5:第三次买入
6:第三次卖出
……
偶数卖出,奇数买入。
1.子状态:dp[i][j],第i天状态j时现金的最大金额
2.?递推状态:
dp[i][0]:
前一天对股票就没操作dp[i-1][0]
dp[i][1]:
前一天没有股票dp[i-1][1],第i天把股票买了dp[i-1][0]-prices[i]
dp[i][2]:
前一天有股票dp[i-1][2],第i天把股票卖出去了dp[i-1][1]+prices[i]
……
dp[i][0] = dp[i - 1][0];
dp[i][1] = max(dp[i - 1][1], prices[i] -?dp[i - 1][0]);? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? dp[i][2]=max(dp[i-1][2],dp[i-1][1]+prices[i]);? ?
……? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
for(int i=1;i<prices.size();i++)
{
for(int j=1;j<2*k+1;j++)
{
if(j%2==0)
dp[i][j]=max(dp[i-1][j-1]+prices[i],dp[i-1][j]);//卖出
else
dp[i][j]=max(dp[i-1][j-1]-prices[i],dp[i-1][j]);//买入
}
}3.初始值:dp[0][0]=0:dp[0][1]-=prices[0],dp[0][3]-=prices[0]……奇数买入,
买入,现金就减少。卖出,现金增加,并且最终取的是最大值,收获利润小于0也没必要计算。
4.遍历顺序:?从前到后
5.返回结果:dp[prices.size()-1][2*k],因为最后一次卖出的价格一定比第一次卖的贵
22.买股票冷冻期
看了好多题解,分了4个状态:今天买,不持有股票有两种:(前天卖今天保持,今天卖 ),今天冷冻期。
感觉还是两种状态简洁一点,也好理解。但上面这种分多种状态讨论的思想要学会。
0:有股票
前一天就有了,前两条天没有今天买了(买入时要考虑冷冻期:昨天是冷冻期,即前天卖了也就是没有股票,今天才能买)。
那么会有i-2,此时要考虑到i<=1时的赋值。
当只有2天,如果可以买卖。只能第一天买,第二天卖,所以一定是前一天已经买好了。
第一天买为负值,第二天不能买了,就得让0状态保持第一天的状态,?比负值还小。
1:没股票
没股票就是卖出了或者是在冷冻期,不需要管前两天的。
前一天没有,即冷冻期或者处于没有状态。
前一天有,今天卖了。
初始值第一天买入即为负值?
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n = prices.size();
if (n == 1) return 0;
vector<vector<int>>dp(n,vector<int>(2,0));
dp[0][0]-=prices[0];
for(int i=1;i<n;i++)
{
//当只有2天,如果可以买卖。只能第一天买,第二天卖,所以一定是前一天已经买好了
//第一天买为负值,第二天不买就得让0状态保持第一天的状态
dp[i][0]=max(dp[i-1][0],(i>1?dp[i-2][1]:0)-prices[i]);
dp[i][1]=max(dp[i-1][1],dp[i-1][0]+prices[i]);
}
return dp[n-1][1];
}
};
23.买股票手续费
比买股票II多了在卖出时减去手续费,因为买卖结束后才算一笔交易,所以不能在买入时就减手续费。
24.最长递增子序列
经典题目!一定要会!
1.子状态:dp[i],前i个字符里最长递增子序列的长度
2.递推状态:如果nums[i]>nums[i-1],dp[i]可由dp[i-1]+1得出,即前i-1个字符再加上第i个字符。
i循环遍历nums数组,令0<= j <=i-1。每次还要比较当前dp[i]和dp[i-1]+1哪一个更大,也就是更新最长子串。
3.初始值:每个字符都设为1个长度。
4.遍历顺序:由dp[i-1]得到所以从前往后。
5.结果:返回的是最长。滚动数组过程中无法确定i遍历完后就是最大,所以要判断遍历完j后当前数组的dp[i]是否最大。
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
if(nums.size()==1)
return 1;
vector<int>a(nums.size(),1);
int c=0;
//0~i-1,i
for(int i=1;i<nums.size();i++)
{
for(int j=0;j<i;j++)
{
if(nums[i]>nums[j])
a[i]=max(a[i],a[j]+1);
}
c=max(c,a[i]);
//由于dp[i]表示前i个字符的最大升序长度。i在外层循环,每一行固定i与每一列的j比大小
//要的是最后结果i,但其他行即i取其他值时有可能升序序列长度更大
}
return c;
}
};25.最长连续递增子序列
关键在于递增,比较dp[i],dp[i-1]的值。递推公式不用再取max了,因为dp[i]意为:以i结尾的递增子序列长度=以i-1结尾的递增序列长度+1。
最终结果要取max,因为自己遍历一遍数组发现最大值不在数组末尾。
递推公式实现后一定要自己算一遍答案。
26.最长公共子序列
1.子状态:两个数组长度不一,采用二维数组分别代表两数组长度。dp[i][j]:n1数组前i个字符与n2数组前j个字符拥有的公共子序列长度。
2.递推状态:题意可知,答案是不连续。从下标1开始。
n1[i-1]与n2[j-1]相等时:dp[i][j]=dp[i-1][j-1]+1。即前从开始到前一个字符得到的最大长度+1
不相等:dp[i][j]=max(dp[i-1][j],dp[i][j-1])?从n1[0,i-2]与n2[0,j-1],n1[0,i-1]与n2[0,j-2]的最长子序列选最大的
3.初始值:0
4.遍历顺序:正序
5.结果dp[n1.size()][n2.size()]
27.判断子序列
编辑距离系列开始啦!
1.子状态:两数组长度不一,采用二维数组分别代表两数组长度。不连续,dp[i][j]:n1数组前i个字符与n2数组前j个字符拥有的公共子序列长度。
2.递推状态:
相等:a[i][j]=a[i-1][j-1]+1;?
不相等:要删除当前字符(j-1),即a[i][j]?要看s[i - 1]与 t[j - 2]的比较结果了:a[i][j] = a[i][j - 1];
3.初始值:a[i][0]表示以i-1为下标结尾的字符串,它与空串的相同序列长度为0
4.遍历顺序:可知a[i][j]来自a[i-1][j-1],a[i][j - 1],所以为正序
5.结果:a[s.size()][t.size()]表示s与t的最长公共序列,如果和s长度相同就得到结果了
其实本题用双指针更简单一点吧~
参考自大佬的题解:
bool isSubsequence(char * s, char * t){
? ? while(*s && *t){
? ? ? ? if(*s == *t){//
? ? ? ? ? ? s++;
? ? ? ? }
? ? ? ? t++;
? ? }
? ? if(*s == '\0')
? ? ? ? return true;
? ? else
? ? ? ? return false;
}
28.不同的子序列?
如果单独拿出来这题,这类题做得少的话,估计不容易想到动态规划的做法(好吧,博主在说博主自己呜呜)。
1.子状态:两个字符串长度不一,二维数组。dp[i][j]为s以下标为i-1?出现和?t以下标j-1结尾的序列相同的个数。
2.递推状态:要得到dp[i][j],注意dp数组从1开始
相等:s[i-1]==t[j-1]:可能使用s[i-1]--->s[0,i-1]匹配t[0,j-1]--->dp[i-1][j-1],也可能不用--->s[0,i]匹配t[j-1],就是去用s数组里 i 前面的字符--->dp[i-1][j]
寻找bat:
babtbat不相等:dp[i][j]=dp[i-1][j],既然不相等,就不用s[i-1]来匹配了。
3.初始值:dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];???dp[i][j] = dp[i - 1][j];??
那么第0行第0列都得初始化:
dp[0][j]:s为空,无法匹配t,=0;
dp[i][0]:t为空,空集是任何字符串的子集,或者理解为,s数组删n个字符,就能得到空串与空串t匹配,=1;
dp[0][0]也和dp[i][0]的理解一致,=1。
4.遍历顺序:来自左上,上面,所以正序。
5.结果:dp[s.size()][t.size()]
放个代码:
发现如果用int类型会溢出,那就用long?long吧。
class Solution {
public:
int numDistinct(string s, string t) {
// dp[0][j]=0;
vector<vector<uint64_t>> dp(s.size() + 1, vector<uint64_t>(t.size() + 1,0));
for(int i=0;i<s.size();i++)
{
dp[i][0]=1;
}
for(int i=1;i<=s.size();i++)
{
for(int j=1;j<=t.size();j++)
{
if(s[i-1]==t[j-1])
{
dp[i][j]=dp[i-1][j-1]+dp[i-1][j];
}
else
{
dp[i][j]=dp[i-1][j];
}
}
}
return dp[s.size()][t.size()];
}
};?29.两个字符串的删除操作
本题可以理解为:两个字符串的公共子序列,最后返回两个数组长度相加-公共子序列*2。就能得到最短操作步数。
两个数组都能删了。
class Solution {
public:
int minDistance(string word1, string word2) {
//最长公共子序列
vector<vector<int>>dp(word1.size()+1,vector<int>(word2.size()+1,0));
for(int i=1;i<=word1.size();i++)
{
for(int j=1;j<=word2.size();j++)
{
if(word1[i-1]==word2[j-1])
dp[i][j]=dp[i-1][j-1]+1;
else
dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
}
}
return word1.size()+word2.size()-dp[word1.size()][word2.size()]*2;
}
};30.编辑距离?
1.子状态:dp[i][j]? w1数组下标i-1结尾,与 以j-1下标结尾的w2,的最近编辑距离。
2.递推状态:
w1[i-1]==w2[j-1]:不操作,就等于dp[i-1][j-1]
w1[i-1]!=w2[j-1]:删除、增加、替换
删除:w1删除1个:dp[i-1][j]+1
删除和增加是一样的:w1: ja 和? w2: a,ja删除j或者a增加j,编辑距离一样?dp[i][j-1]+1
替换:w1替换掉w1[i-1],让他与w2[j-1]相等,即w1数组下标i-2结尾,与 以j-2下标结尾的w2,的最近编辑距离。dp[i-1][j-1]+1,在进行替换的数组里:dp[i-1][j-1]表示前面的已经相等了,再加当前i-1下标的字符被替换。
3.初始值:
dp[i][0]:以下标i-1的w1,与空字符串的?最短编辑距离:删除i个
dp[0][j]:以下标j-1的w2,与空字符串的?最短编辑距离:删除j个
4.遍历顺序:
来自左边,上边,左上,所以正序
5.结果:遍历一遍即可得到最后的答案在尾部。
31.回文子串
动态规划和双指针都行,先来看看双指针:
分别以s的每个字符为中心点,向两边扩散,找两边相等的,这是奇数个字符时的做法。
偶数个字符,比如caac,则要以两个中心字符向两边扩散。
?
动态规划:
1.子状态:dp[i][j]:[i,j]闭区间内是否为回文子串
2.递推状态:
s[i]==s[j]:
①i==j:a是回文子串
②i+1=j:aa也是
③j-1>i:已经s[i]==s[j],下标i与j差了很多,隔了很远,就得缩短空间-->dp[i+1][j-1]判断是否文回文子串。
s[i]!=s[j]:
dp[i][j]=false
3.初始值:
都为false
4.遍历顺序:
dp[i][j]由dp[i+1][j-1],也就是左下方推出,就得从下往上遍历。
5.结果:
数一数总共几个true
class Solution {
public:
int countSubstrings(string s) {
vector<vector<bool>>a(s.size(),vector<bool>(s.size()+1,false));
int c=0;
for(int i=s.size()-1;i>=0;i--)
{
for(int j=i;j<s.size();j++)
{
if(s[i]==s[j])
{
if(j-i<=1)
{
c++;
a[i][j]=true;
}
else if(a[i+1][j-1])
{
a[i][j]=true;
c++;
}
}
}
}
return c;
}
};
32.最长回文子序列
1.子状态:dp[i][j],区间内回文子序列的长度
2.递推状态:
s[i]==s[j]:
dp[i][j]=dp[i+1][j-1]+2:加上相等的两字符
s[i]!=s[j]:
更新最大值,dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);? 既然两边不相等,那就去掉一边看看是否能为最大值。
s[i]? ?s[i+1]? ? s[j-1]? ?s[j]
3.初始值:
式子无法推出dp[i][i],那就初始为1,其他都为0.
4.遍历顺序:
来自左下,左,下。从下往上遍历。
5.结果:
下->上遍历,左->右,结果应该在右上角。dp[0][s.size()-1]
如果对你有帮助,请一键三连(点赞+收藏+关注)哦~ 感谢支持!让更多的人看到~ 欢迎各位在评论区与博主友好讨论!(????)

?
?(表情包来源网络)
