2022年春季学期《算法分析与设计》练习10
文章目录
最长递增子序列
题目描述
给定一个序列 a,求去除 a 中一段连续长度为 L 的序列后,a 的最长不下降子序列的长度的最大值。
输入
单组数据。
第一行两个整数 n,L 表示序列的长度为 n,L 如题意所示。
第二行 n 个数表示序列 a
n ≤ 105, 0 ≤ L ≤ n
输出
输出一个整数表示最长不下降子序列长度的最大值
样例输入
6 3
2 1 3 6 4 5
样例输出
3
分析:如果序列长度为1,那么最长递增子序列也为1;
如果序列长度不为1,那么我们需要在前面找一个a[j]<a[i],并且以a[j]结尾的所得到的最长递增子序列长度最大,那么可以利用这个a[j]对应的长度b[j]+1,这样一直遍历下去就可以得到最长递增子序列。
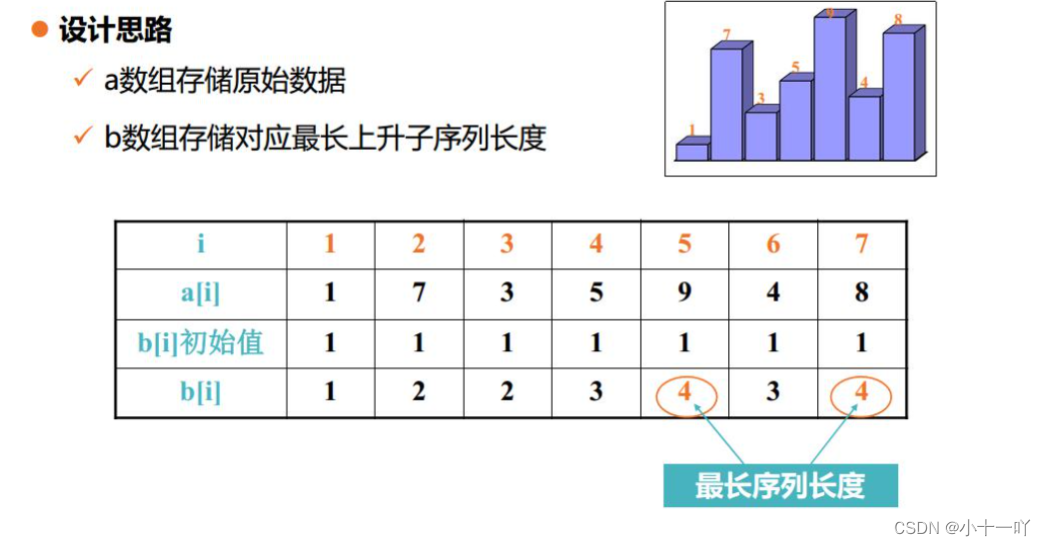
不过这个题目老师给我们讲的是时间复杂度为O(n^2)的代码分析,优化后的代码的时间复杂度为O(nlogn)。
O(n^2):
#include <bits/stdc++.h>
using namespace std;
int solve(int a[],int dp[],int n)
{
dp[0]=1;
int maxlen;
int maxx=dp[0];
for(int i=1; i<n; i++)
{
maxlen=0;
for(int j=i-1; j>=0; j--)
{
if(a[j]<a[i]&&maxlen<dp[j])
{
maxlen=dp[j];
}
}
dp[i]=maxlen+1;
if(dp[i]>maxx)
maxx=dp[i];
}
return maxx;
}
int main()
{
int a[2005],dp[2005];
int n;
while(cin>>n)
{
for(int i=0; i<n; i++)
{
cin>>a[i];
}
cout<<solve(a,dp,n)<<endl;
}
}
O(nlogn):
#include <bits/stdc++.h>
using namespace std;
const int N = 100010;
int a[N],b[N];
int q[N];//所有不同长度上升子序列最小值
int n,m;
int main()
{
while(cin>>n)
{
for (int i = 0; i < n; i ++ )cin>>a[i];
int len = 0;
for (int i = 0; i < n; i ++ )
{
int l = 0,r = len;
//l到r之间小于a[i]最大的数
while(l < r)
{
int mid = l + r + 1>> 1;//右移1位相当于除以2
if(q[mid] < a[i])l = mid;
else r = mid - 1;
}
len = max(len,r + 1);
q[r + 1] = a[i];
}
cout<<len<<endl;
}
return 0;
}
构造最长递增子序列
题目描述
在“最长递增子序列”的基础上对代码进行改进,输出一条最长递增子序列。
输入
每组输入包括两行,第一行为序列长度n,第二行为序列。
输出
输出最长递增子序列中的任意一条即可。
样例输入
7
1 7 3 4 9 2 3
样例输出
1 3 4 9
构造最长递增子序列相对于第一题需要引入一个新的数组pre数组,把找到的a[j]<a[i],并且以a[j]结尾的所得到的最长递增子序列长度最大的这个值 的下标保存在pre数组中,然后再对pre数组遍历拿出对应的a数组中的值输出即可.
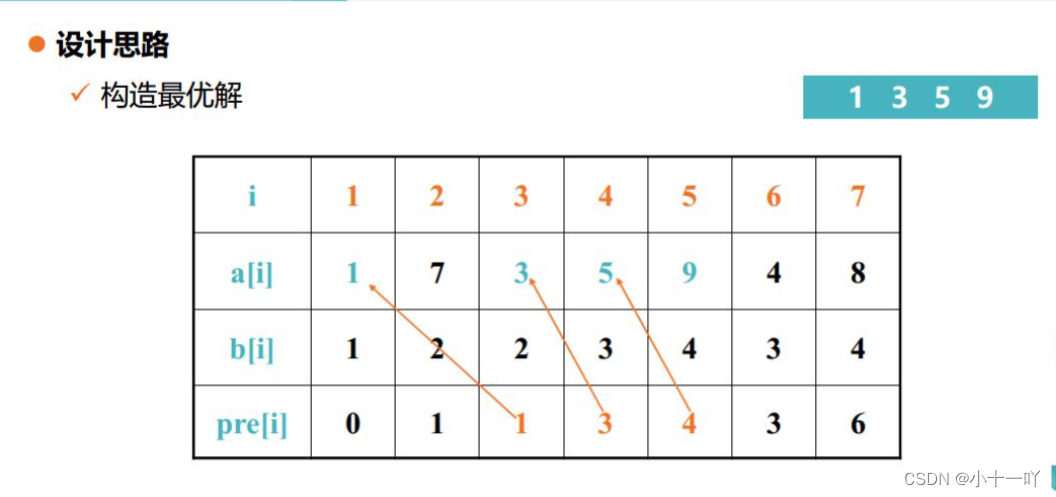
#include <bits/stdc++.h>
using namespace std;
int p[2005];
int solve(int a[],int dp[],int n)
{
dp[0]=1;
int maxlen;
int maxx=dp[0];
int x=0;
for(int i=1; i<n; i++)
{
maxlen=0;
for(int j=i-1; j>=0; j--)
{
if(a[j]<a[i]&&maxlen<dp[j])
{
maxlen=dp[j];
p[i]=j;
}
}
dp[i]=maxlen+1;
if(dp[i]>maxx)
{
maxx=dp[i];
x=i;
}
}
int i=x;
int m=maxx;
int c[2000];
while(m>0)
{
c[m]=a[i];
i=p[i];
m--;
}
for(int i=1; i<=maxx; i++)
if(i==maxx)
{
printf("%d\n",c[i]);
}
else
{
printf("%d ",c[i]);
}
}
int main()
{
int a[2005],dp[2005];
int n;
while(cin>>n)
{
for(int i=0; i<n; i++)
{
cin>>a[i];
}
solve(a,dp,n);
}
}
出列人数
题目描述
有N位同学站在一排,体育老师要请其中的(N-K)位同学出列,将剩下的K位同学从左到右依次编号为1,2,3,…K,他们的身高分别为T1,T2,T3,…TK,要求满足T1<T2<T3<…<TK。已知N位同学的身高,请设计一个算法,计算最少需要几位同学出列可使得剩下的同学满足上述要求。
输入
多组输入,对于每一组测试数据,第1行N表示同学数量(n<=1000)。
第2行包含N个正整数,分别表示每一个同学的身高。(单位:厘米)
输出
输出最少需要出列的同学人数。
样例输入
4
172 185 169 178
5
165 168 174 170 182
样例输出
2
1
这个题目的代码和最长递增子序列的代码可以说是一模一样了。只不过输出的时候是需要输出不符合的人数,即把除了可以构成最长递增子序列的数字长度减掉就是最后输出的答案。即:n-len,len为最长递增子序列的长度。
#include <bits/stdc++.h>
using namespace std;
int solve(int a[],int dp[],int n)
{
dp[0]=1;
int maxlen;
int maxx=dp[0];
for(int i=1; i<n; i++)
{
maxlen=0;
for(int j=i-1; j>=0; j--)
{
if(a[j]<a[i]&&maxlen<dp[j])
{
maxlen=dp[j];
}
}
dp[i]=maxlen+1;
if(dp[i]>maxx)
maxx=dp[i];
}
return maxx;
}
int main()
{
int a[2005],dp[2005];
int n;
while(cin>>n)
{
for(int i=0; i<n; i++)
{
cin>>a[i];
}
cout<<n-solve(a,dp,n)<<endl;
}
}
0-1背包问题
题目描述
给定n种物品和一个背包,物品i的重量是Wi,其价值为Vi,背包的容量为C。如何选择装入背包的物品,可以使得装入背包中物品的总价值最大?
输入
每组输入包括三行,
第一行包括物品个数n,以及背包容量C。
第二、三行包括两个一维数组,分别为每一种物品的价值和重量。
输出
输出包括两行,第一行为背包的最大总价值,第二行为所选取的物品。
例如:最大总价值=15,物品选取策略为11001。数据保证答案唯一。
样例输入
5 10
6 3 5 4 6
2 2 6 5 4
样例输出
15
11001
根据是否可以放入来求得递归式:
不放:背包当前产生价值仍为dp(i+1,j)
放入:调整背包容量j-wi,背包当前产生价值为m(i+1,j-wi)+vi;
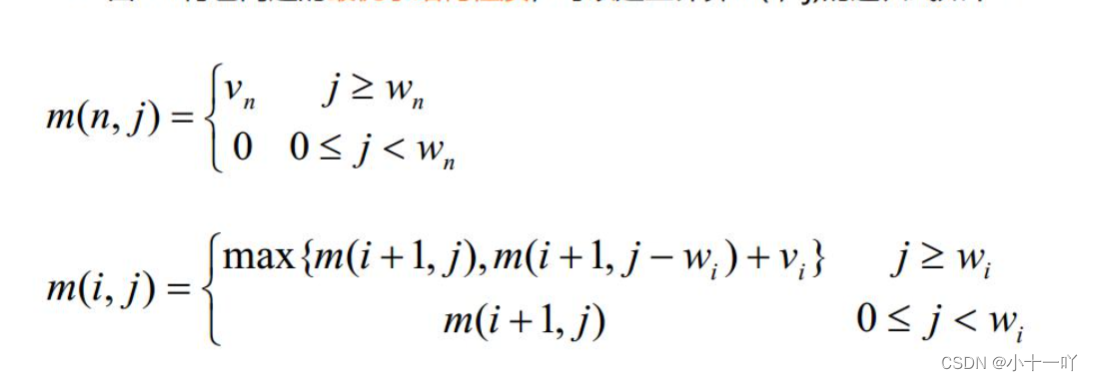
#include <bits/stdc++.h>
using namespace std;
int dp[2010][2010];
void solve(int w[],int v[],int n,int c)
{
int jmax=min(w[n]-1,c);
for(int j=0; j<=jmax; j++)
{
dp[n][j]=0;
}
for(int j=w[n]; j<=c; j++)
{
dp[n][j]=v[n];
}
for(int i=n-1; i>=1; i--)
{
int jmax=min(w[i]-1,c);
for(int j=0; j<=jmax; j++)
{
dp[i][j]=dp[i+1][j];
}
for(int j=w[i]; j<=c; j++)
{
dp[i][j]=max(dp[i+1][j],dp[i+1][j-w[i]]+v[i]);
}
}
}
void print(int w[],int c,int n)
{
for(int i=1; i<=n; i++)
{
if(dp[i][c]==dp[i+1][c])
{
cout<<"0";
}
else
{
c-=w[i];
if(c>=0)
{
cout<<"1";
}
else
{
cout<<"0";
}
}
}
}
int main()
{
int n,c;
int v[2005],w[2005];
while(cin>>n>>c)
{
for(int i=1; i<=n; i++)
{
cin>>v[i];
}
for(int i=1; i<=n; i++)
{
cin>>w[i];
}
solve(w,v,n,c);
cout<<dp[1][c]<<endl;
print(w,c,n);
cout<<endl;
}
return 0;
}
XP的午餐
题目描述
XP每天都会思考一个问题,今天午餐去哪里吃?这是一个很重要的问题,这会影响到他下午的体力值。他的午餐预算是M元,现在有N种菜品,每一种菜品的价格和能够提供的体力值已知(每种菜品只能选择一次),请问如何选择菜品能够让XP下午的体力值最大呢?
输入
多组输入
第一行:M元和菜品数量N。
接下来N行,每一行两个整数,分别表示每一种菜品的价格(vi)和能够获得的体力值(wi)。
(0<N<=20,0<=M<=1000)(0<=vi<=50,0<=wi<=100)
输出
最大体力值。
样例输入
10 5
1 5
2 4
3 3
4 2
5 1
样例输出
14
这题和后面一题都是利用01背包问题做的文章,理解了01背包就行。直接贴代码吧。
#include <bits/stdc++.h>
using namespace std;
int dp[2010][2010];
struct Node
{
int v;
int w;
} p[2005];
int main()
{
int n,c;
int v[2005],w[2005];
while(cin>>c>>n)
{
for(int i=1; i<=n; i++)
{
cin>>p[i].v>>p[i].w;
}
int jmax=min(p[n].v-1,c);
for(int j=0; j<=jmax; j++)
{
dp[n][j]=0;
}
for(int j=p[n].v; j<=c; j++)
{
dp[n][j]=p[n].w;
}
for(int i=n-1; i>=1; i--)
{
int jmax=min(p[i].v-1,c);
for(int j=0; j<=jmax; j++)
{
dp[i][j]=dp[i+1][j];
}
for(int j=p[i].v; j<=c; j++)
{
dp[i][j]=max(dp[i+1][j],dp[i+1][j-p[i].v]+p[i].w);
}
}
cout<<dp[1][c]<<endl;
}
return 0;
}
补充能量
题目描述
一年一度的宇宙超级运动会在宇宙奥特英雄体育场隆重举行。X星人为这场运动会准备了很长时间,他大显身手的时刻终于到了!
为了保持良好的竞技状态和充沛的体能,X星人准备了N个不同的能量包,每个能量包都有一个重量值和能量值。由于这些能量包的特殊性,必须要完整地使用一个能量包才能够发挥功效,否则将失去能量值。
考虑到竞赛的公平性,竞赛组委会规定每个人赛前补充的能量包的总重量不能超过W。
现在需要你编写一个程序计算出X星人能够拥有的最大能量值是多少?
输入
单组输入。
第1行包含两个正整数N和W,其中N<=103,W<=103。
第2行包含N个正整数,分别表示每一个能量包的重量,两两之间用空格隔开。
第3行包含N个正整数,分别表示每一个能量包的能量值,两两之间用空格隔开。
输出
输出X星人能够拥有的最大能量值。
样例输入
3 10
4 5 7
100 120 200
样例输出
220
这个题目由于我是直接套用的构造01背包为题的代码,所以对于这个题目,代码里面的print函数用不到。
#include <bits/stdc++.h>
using namespace std;
int dp[2010][2010];
void solve(int w[],int v[],int n,int c)
{
int jmax=min(w[n]-1,c);
for(int j=0; j<=jmax; j++)
{
dp[n][j]=0;
}
for(int j=w[n]; j<=c; j++)
{
dp[n][j]=v[n];
}
for(int i=n-1; i>=1; i--)
{
int jmax=min(w[i]-1,c);
for(int j=0; j<=jmax; j++)
{
dp[i][j]=dp[i+1][j];
}
for(int j=w[i]; j<=c; j++)
{
dp[i][j]=max(dp[i+1][j],dp[i+1][j-w[i]]+v[i]);
}
}
}
/*void print(int w[],int c,int n)
{
for(int i=1; i<=n; i++)
{
if(dp[i][c]==dp[i+1][c])
{
cout<<"0";
}
else
{
c-=w[i];
if(c>=0)
{
cout<<"1";
}
else
{
cout<<"0";
}
}
}
}*/
int main()
{
int n,c;
int v[2005],w[2005];
while(cin>>n>>c)
{
for(int i=1; i<=n; i++)
{
cin>>w[i];
}
for(int i=1; i<=n; i++)
{
cin>>v[i];
}
solve(w,v,n,c);
cout<<dp[1][c]<<endl;
/*print(w,c,n);
cout<<endl;*/
}
return 0;
}
最少硬币
题目描述
假设有4种硬币,它们的面值分别为1分、5分、10分和25分。
现在要找给顾客n分钱。
请问怎样找零钱才能使给顾客的硬币个数最少?
输出所需最少硬币的枚数。
输入
输入需要找给顾客的零钱n(单位:分)。
输出
输出所需最少硬币的枚数。
样例输入
8
10
63
样例输出
4
1
6
这个是最最简单的贪心问题了。就是根据硬币的面值来计算,从面值最大的开始贪。
不过这里老师跟我们说了并不是所有的硬币问题都可以使用贪心算法,
对于面值成等比数列的硬币问题一定可以使用贪心算法,而对于面值不成等比数列的硬币问题则不一定能使用贪心算法。
而对于硬币问题除了可以使用贪心算法外,还可以使用动态规划来写,并且对硬币的面值没有要求。下面我会贴上贪心算法的代码以及动态规划方法的代码。
贪心算法:
#include <bits/stdc++.h>
using namespace std;
const int a[4]= {1,5,10,25};
int main()
{
int n;
while(cin>>n)
{
int j=3;
int ans=0;
while(n>0)
{
if(n>=a[j])
{
ans++;
n-=a[j];
}
else
{
j--;
}
}
cout<<ans<<endl;
}
return 0;
}
动态规划:
#include<bits/stdc++.h>
using namespace std;
int main()
{
int v[4] = {1,5,10,25};
int n;
while(cin>>n)
{
int length = sizeof(v) / sizeof(v[0]);
int *dp = new int [n + 1]();
for (int i = 1; i <= n; ++i)
{
dp[i] = i;
for (int j = 0; j < length; ++j)
{
if (i >= v[j] && dp[i] > (1 + dp[i - v[j]]))
{
dp[i] = 1 + dp[i - v[j]];
}
}
}
cout <<dp[n]<<endl;
}
return 0;
}
图书排序
题目描述
某图书销售管理系统需要对图书(Book)进行排序,每一本图书包含书名(bookName)、销量(bookSales)、价格(bookPrice)等属性,要求先按照销量由大到小排序,对于销量相同的图书再按照价格由小到大排序。
输入
每组输入包括两个部分,第一部分为书的数量n,
接下来n行则为n本书的信息。 按顺序输入书名(不超过20个字)、销量、价格。
输出
输出排序后的信息,每个属性用空格隔开
样例输入
7
C++程序设计 120 25.00
软件工程 96 48.00
高等数学 80 32.50
算法分析与设计 96 54.00
离散数学 96 28.00
计算机网络 96 36.00
操作系统 115 45.00
样例输出
C++程序设计 120 25.00
操作系统 115 45.00
离散数学 96 28.00
计算机网络 96 36.00
软件工程 96 48.00
算法分析与设计 96 54.00
高等数学 80 32.50
根据题目意思来就行了。
#include <bits/stdc++.h>
using namespace std;
struct Node
{
string bn;
int bs;
double bp;
} p[2010];
bool cmp(Node a,Node b)
{
if(a.bs!=b.bs)
{
return (a.bs>b.bs);
}
else
{
return (a.bp<b.bp);
}
}
int main()
{
int n;
while(cin>>n)
{
for(int i=0; i<n; i++)
{
cin>>p[i].bn>>p[i].bs>>p[i].bp;
}
sort(p,p+n,cmp);
for(int i=0; i<n; i++)
{
cout<<p[i].bn<<" ";
printf("%d %.2lf\n",p[i].bs,p[i].bp);
}
}
return 0;
}
道具的魅力值
题目描述
在某网络游戏中提供了一个道具库,在道具库中每种道具均有若干件(数量已知),游戏玩家购买一件道具将获得一定的魅力值。
已知每种道具的价格和魅力值,请编写一个程序,在总价格不超过某个上限的情况下使得所购道具的魅力值之和达到最大。
输入
每组测试数据的输入有n+1行,n表示道具的种类。(n<=100,p<=10000)
第1行包含两个正整数,分别表示道具种类数n和总价值的上限p,两个数字之间用空格隔开。
第2行到第n+1行分别对应于第1种道具到第n种道具的信息,每1行包含三个正整数,两个数字之间用空格隔开,三个正整数分别表示某一种道具的数量、单个道具的价格和魅力值。
输出
每组测试数据的输出只有一行,即道具魅力值的最大和。
样例输入
3 10
2 2 3
1 5 10
2 4 12
样例输出
27
多重背包问题这里贴个链接吧,学习多重背包问题的视频:
下面贴上代码:
#include<bits/stdc++.h>
using namespace std;
int v[510],w[510],s[510],dp[10020];
int main(){
int n,m;
while(cin>>n>>m){
for(int i=1;i<=n;i++){
cin>>s[i]>>v[i]>>w[i];
}
for(int i=1;i<=n;i++){
for(int j=m;j>=1;j--){
for(int k=0;k<=s[i]&&j>=k*v[i];++k){
dp[j]=max(dp[j],dp[j-k*v[i]]+k*w[i]);
}
}
}
cout<<dp[m]<<endl;
}
}
最长不下降子序列
题目描述
给定一个序列 a,求去除 a 中一段连续长度为 L 的序列后,a 的最长不下降子序列的长度的最大值。
输入
单组数据。
第一行两个整数 n,L 表示序列的长度为 n,L 如题意所示。
第二行 n 个数表示序列 a
n ≤ 105, 0 ≤ L ≤ n
输出
输出一个整数表示最长不下降子序列长度的最大值
样例输入
6 3
2 1 3 6 4 5
样例输出
3
这个题目是真不会啊,属实是小菜鸡。。。。
