二叉搜索树的第k大节点

题目链接：https://leetcode-cn.com/problems/er-cha-sou-suo-shu-de-di-kda-jie-dian-lcof/

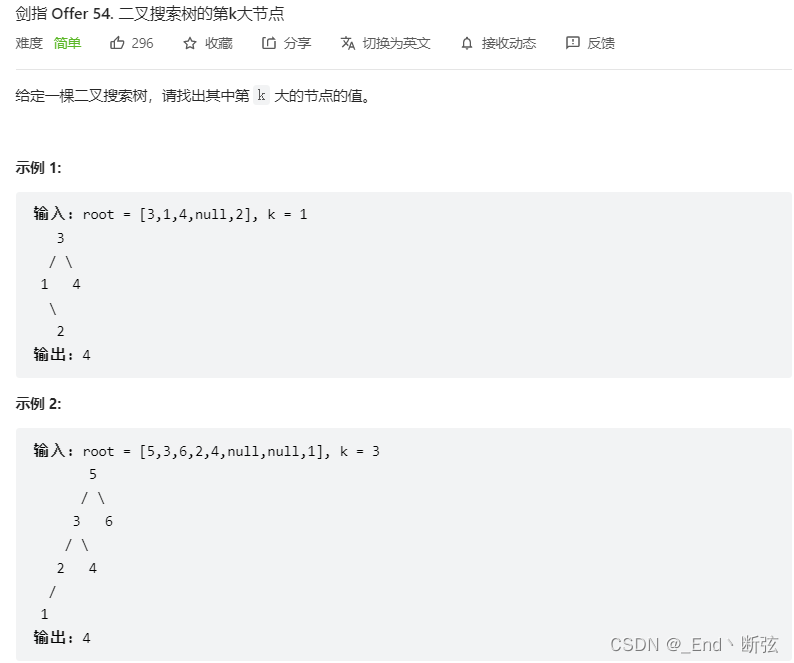
在这里插入图片描述

二叉搜索树性质：左子节点比根节点小，右子节点比根节点大，中序遍历出来是升序的，题目是求第K个大的结点，可以转化为求中序的遍历倒序的第K个结点,先递归右子树，k–，再递归左子树

动图演示：

代码如下：

class Solution {
public:
   int ans;
    int kthLargest(TreeNode* root, int k) {
        dfs(root,k);
        return ans;
    }
    void dfs(TreeNode* root,int &k)
    {
        if(!root) return;//结点为空结束
        
        dfs(root->right,k);//先递归右子树
        k--;
       
        if(!k) ans = root->val;// k == 0记录答案
        if(!k) return;// 返回，就不用再到左子树递归
        dfs(root->left,k);
    }
};

在这里插入图片描述

时间复杂度:O(N),空间复杂度:O(N)

二叉搜索树的最近公共祖先

题目链接：https://leetcode-cn.com/problems/er-cha-sou-suo-shu-de-zui-jin-gong-gong-zu-xian-lcof/

在这里插入图片描述

之前讲过普通二叉树的最近公共祖先，这里是搜索树就变得简单了：

代码如下：

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(!root) return nullptr;
        
        //找到一个比q大比p小的或者比q小比p大就返回，否则递归处理左右子树
        if((p->val <= root->val && q->val >= root->val) ||
           (p->val >= root->val && q->val <= root->val)) return root;
        else if(p->val <= root->val && q->val <= root->val)
            return lowestCommonAncestor(root->left,p,q);
        else
           return lowestCommonAncestor(root->right,p,q);
    }
};

在这里插入图片描述

时间复杂度:O(N),最坏的情况是退化成链表
空间复杂度度:O(N)

和为s的两个数字

题目链接：https://leetcode-cn.com/problems/he-wei-sde-liang-ge-shu-zi-lcof/

在这里插入图片描述

首先想到的是用哈希表来做，如果能在哈希表中找到就返回对应的索引，否则返回空

 unordered_set<int> sumHash;
        for(int i : nums)
        {
            if(sumHash.count(target - i))
            return vector<int>{i,target - i};
            sumHash.insert(i);
        }
        return vector<int>();

提交过后看了一下，太慢了，看了一下大佬们的题解，对撞双指针了解一下：

代码如下：

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        int left = 0, right = nums.size()-1;
        while(left < right)
        {
           int sum = nums[left] + nums[right];
           if(sum > target) right--;
           else if(sum < target) left++;
           else return vector<int>{nums[left],nums[right]};
        }
         return vector<int>();
       
    }
};

时间复杂度:O(N),空间复杂度:O(1)，哈希表的时间复杂度O(N),空间复杂度:O(N)

扑克牌中的顺子

题目链接：https://leetcode-cn.com/problems/bu-ke-pai-zhong-de-shun-zi-lcof/

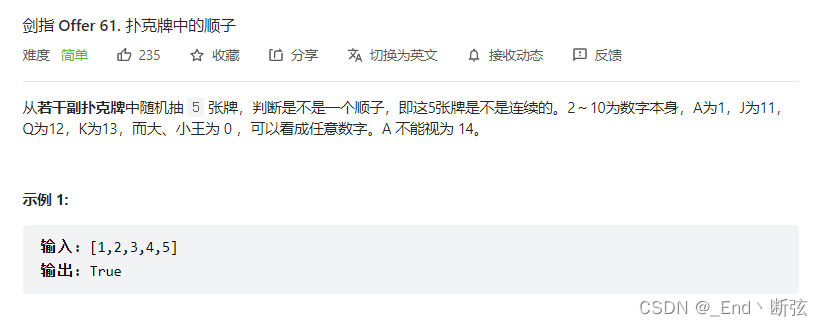
在这里插入图片描述

1.先将数组排序
2.把0去掉，遍历数组，有重复的牌返回false
3.若最大值-最小值小于等于4则是true，否则false

代码如下：

class Solution {
public:
    bool isStraight(vector<int>& nums) {
        if(nums.empty()) return false;
        sort(nums.begin(),nums.end());
        int k = 0;
        while(!nums[k]) k++;//去掉0
        for(int i = k + 1;i < nums.size();++i)
        {
            if(nums[i] == nums[i-1])//判断是否有重复的元素
            return false;
        }
        return *(nums.end()-1) - nums[k] <= 4;
    }
};

时间复杂度;O(nlogn),空间复杂度:O(1),还可以用set做

class Solution {
public:
    bool isStraight(vector<int>& nums) {
        if(nums.empty()) return false;
          set<int> s;
        for(int i = 0; i < nums.size(); i++) {
            if(nums[i] == 0) {//去掉0
                continue;
            }
            if(s.count(nums[i])) {//去掉重复的
                return false;
            }
            s.insert(nums[i]);
        }
        return *(--s.end()) - *s.begin() <= 4;  
    }
};