前言
快速排序是一种不稳定的、 时间复杂度为O(nlogn)的排序算法,算是较快的算法。
类似于归并排序,主要思想是分治,不同的是快排自顶向下(类似于二叉树的前序遍历),归并排序自底向上(类似于二叉树的后序遍历)。
时间复杂度:
平均:
O
(
n
l
o
g
n
)
O(nlogn)
O(nlogn)
最坏:
O
(
n
2
)
O(n^2)
O(n2)
最好:
O
(
n
l
o
g
n
)
O(nlogn)
O(nlogn)
空间复杂度:
平均:
O
(
l
o
g
n
)
O(logn)
O(logn)
最坏:
O
(
n
)
O(n)
O(n)
快速排序
原理
快排的基本概念就是选取一个目标元素,然后将目标元素放到数组中正确的位置,然后根据该元素,将数组切分成两个子数组(相对有序,组间有序,组内无序),用相同的方法,在没有排好序的范围进行相同操作。
一趟排序将待排序的数列分成两部分,其中一部分元素都比另一部分小,再分别对这两部分数列进行排序,以达到整个数列有序。
图示
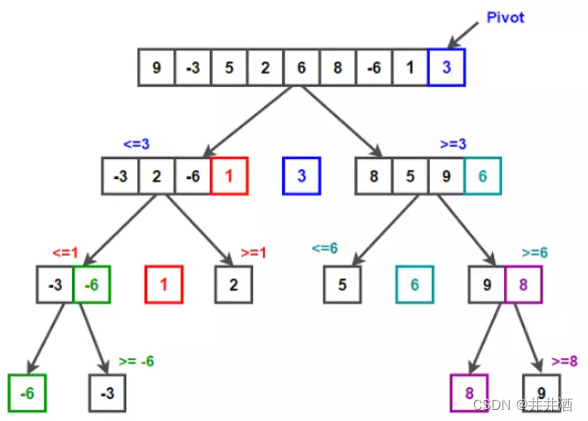

代码实现
具体步骤
- 对当前数组,选一个元素,作为基准privot;(常取第一个元素或最后一个元素)
- 分区:重新排序数列,将所有比基准小的数放在基准前面,所有比基准大的放在基准后面,相同的可以任意一边。分区后。基准元素处于数列的中间;
- 根据基准的位置将原数组分成前后两个子数组;
- 对两个子数组采用以上全部步骤,直到子数组的长度小于等于1为止。
实现代码
void Sort::quick_sort(vector<int>& nums, int l, int r){
int n = nums.size();
if (l < r) {
int index = part(nums, l, r); //一趟排序,并返回交换后基数下标
quick_sort(nums, l, index - 1); //递归排序左边数组
quick_sort(nums, index + 1, r); //递归排序右边数组
}
}
int Sort::part(vector<int>& nums, int l, int r) {
int p = nums[l]; //数组第一个元素作为基准
int i = l, j = r;
while (i < j) {
while (nums[j] >= p && i < j) j--; //从右往左找第一个小于基准的数
while (nums[i] <= p && i < j) i++; //从左往右找第一个大于基准的数
swap(nums[i], nums[j]); //交换两个数
}
swap(nums[i], nums[l]); //把找到的小于基准的数与基数交换,这样小数就换到基准前面
return i;
}
复杂度分析
时间复杂度
最坏
O
(
n
2
)
O(n^2)
O(n2), 平均
O
(
n
l
o
g
n
)
O(nlogn)
O(nlogn):最坏情况下,元素一开始就是从大到小排列的,那么每个元素都需要调换,时间复杂度就是
O
(
n
2
O(n^2
O(n2)。正常情况下,需要切分logn次,每层的划分是O(n),就是
O
(
n
l
o
g
n
)
O(nlogn)
O(nlogn)。
空间复杂度
最坏
O
(
n
)
O(n)
O(n),平均
O
(
l
o
g
n
)
O(logn)
O(logn):空间复杂度取决于递归的层数,最糟糕的情况需要O(n)层,平均O(logn)。
总结
快速排序采用分治思想,先划分子序列,让子序列间有序,在让子序列内有序。
时间复杂度:
平均:
O
(
n
l
o
g
n
)
O(nlogn)
O(nlogn)
最坏:
O
(
n
2
)
O(n^2)
O(n2)
最好:
O
(
n
l
o
g
n
)
O(nlogn)
O(nlogn)
空间复杂度:
平均:
O
(
l
o
g
n
)
O(logn)
O(logn)
最坏:
O
(
n
)
O(n)
O(n)
