前言:
本篇主要记录堆排序及TOP-K问题的求解
目录
1.1.1 向上调整算法建堆的时间复杂度 O(N*logN)
1、堆的应用
1.1 堆排序
堆排序即利用堆的思想来进行排序,总共分为两个步骤:
1. 建堆
升序:建大堆
降序:建小堆建的是大堆还是小堆取决于向上调整和向下调整中的判断语句
2. 利用堆删除思想来进行排序建堆和堆删除中都用到了向下调整,因此掌握了向下调整,就可以完成堆排序
1.1.1 向上调整算法建堆的时间复杂度 O(N*logN)
向上调整算法思想:
从第二个节点开始,向上调整一次,可保证这个节点及之前节点构成一个堆;找到下一个节点,调用一次向上调整,又能保证这个节点及之前所有节点构成一个堆,循环往复,对最后一个节点调用向上调整时,能保证所有节点构成一个堆。
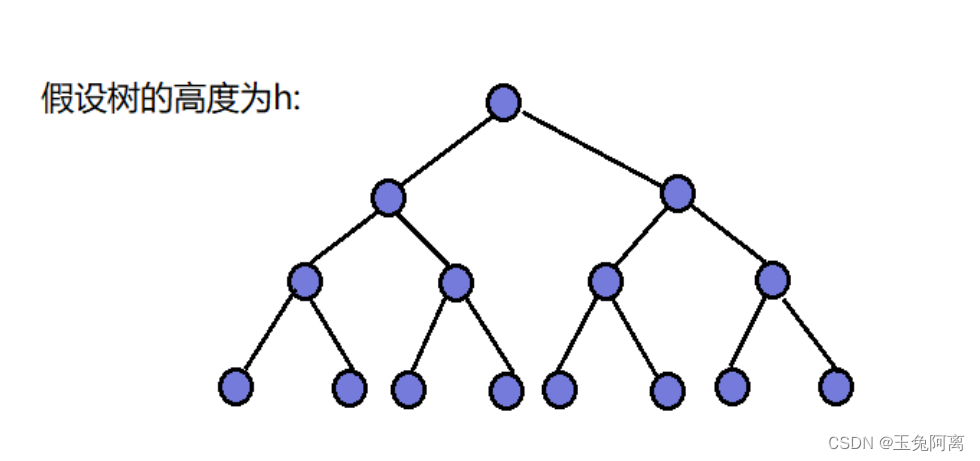
??? 即? ?
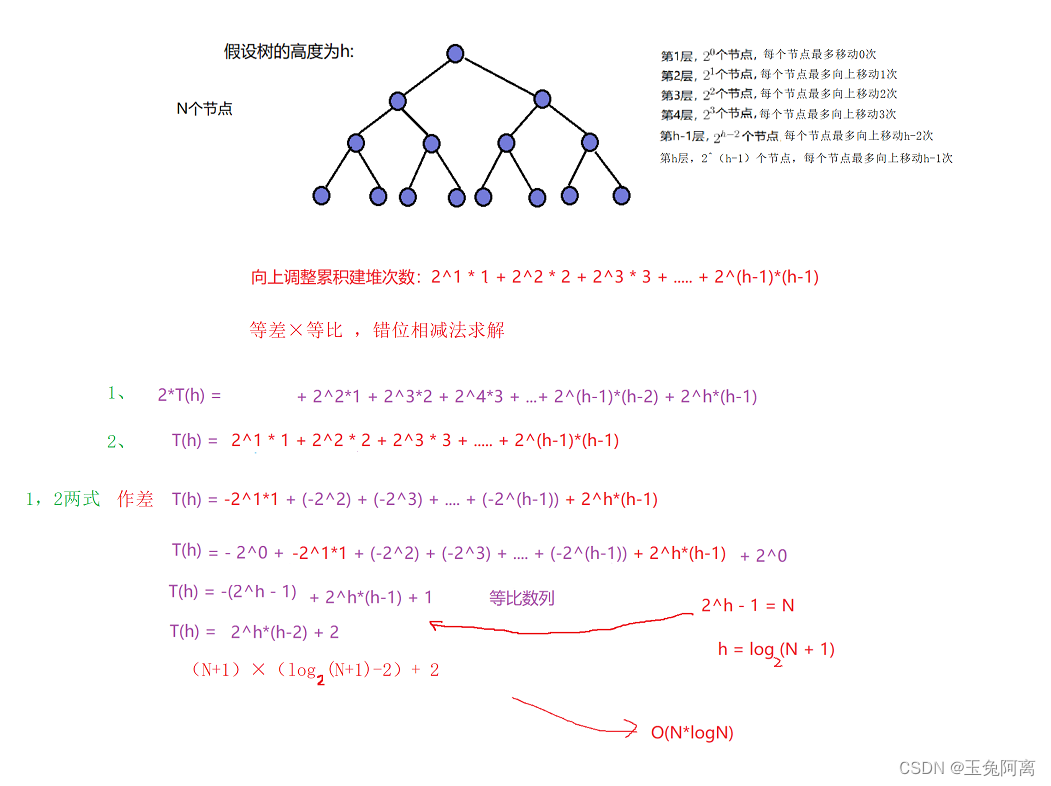 ?
?
//向上调整算法建一个堆
for (int i = 1; i < n; i++)
{
AdjustUp(a, i);
}1.1.2 向下调整算法建堆的时间复杂度 O(N)
向下调整算法的思想:
在向下调整中,要保证左子树和右子树均是堆,否则不能;按照这个思路,那采用向下调整建堆时,应该从下往上走,保证左右子树都是堆。
找到最后一个非叶节点(最后一个节点的父亲),调用一次向下调整;再找到前一个节点,调用一次向下调整,循环往复,直到对根节点向下调整(此时根节点的左右子树已是堆),堆就实现了。
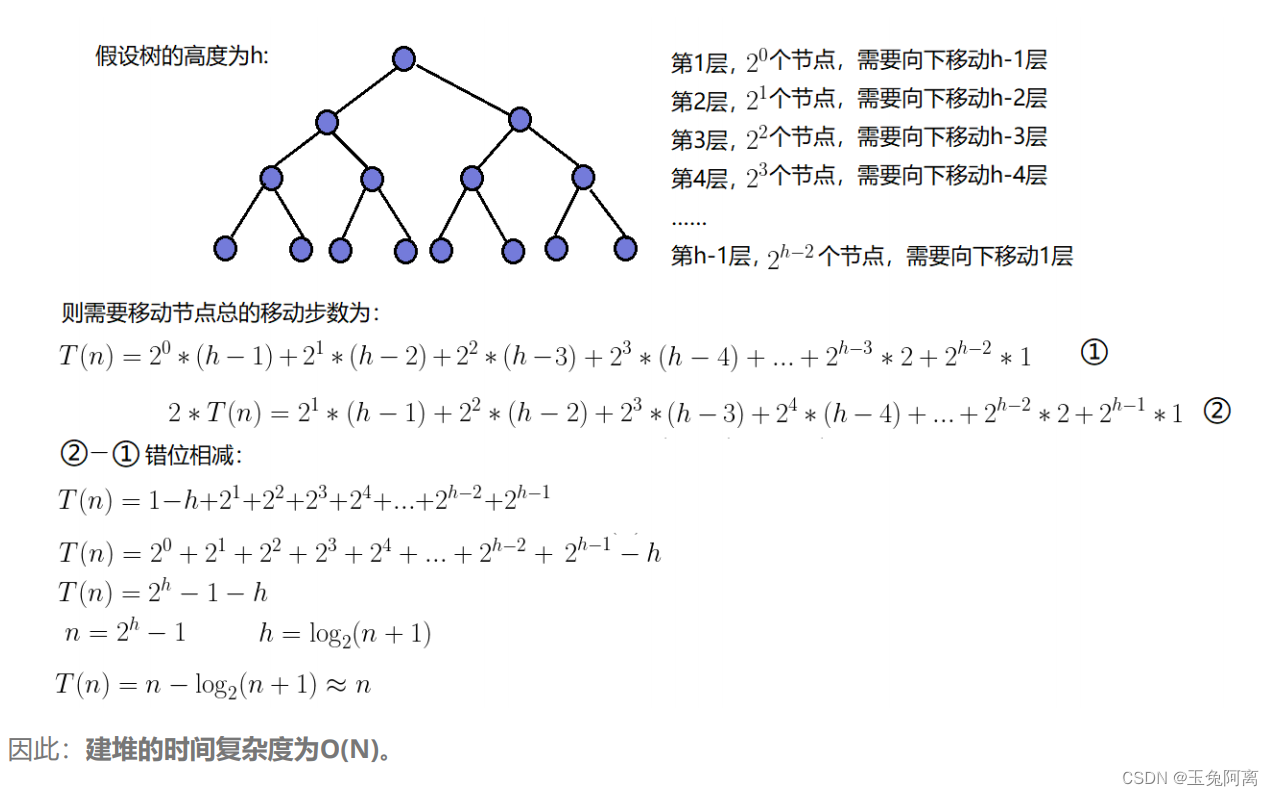 ?
?
//用向下调整算法建一个堆
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(a, n, i);
}?相对于向上调整算法和向下调整算法的时间复杂度,建堆选择向下调整算法
1.1.3?堆排序?
堆排序思想:
1、建一个堆,有两种方法:循环调用向上调整或者循环调用向下调整
2、利用堆删除思想,将堆顶元素和最后一个元素交换,对前 n - 1?个节点向下调整,循环往复
时间复杂度O(N *?logN)
空间复杂度O(1),对原数组进行排序,未开辟新空间
void HeapSort(int* a, int n)
{
//向上调整算法建一个大堆
for (int i = 1; i < n; i++)
{
AdjustUp(a, i);
}
//用向下调整算法建一个大堆
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(a, n, i);
}
size_t end = n - 1;
while (end > 0)
{
Swap(&a[0], &a[end]);
AdjustDown(a, end, 0);
end--;
}
}
1.2 TOP-K问题
即求数据结合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大。
比如:专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。
对于Top-K问题,能想到的最简单直接的方式就是排序,但是:如果数据量非常大,排序就不太可取了(可能数据都不能一下子全部加载到内存中)。最佳的方式就是用堆来解决,基本思路如下:
1. 用数据集合中前K个元素来建堆
前k个最大的元素,则建小堆
前k个最小的元素,则建大堆
2. 用剩余的N-K个元素依次与堆顶元素来比较,不满足则替换堆顶元素将剩余N-K个元素依次与堆顶元素比完之后,堆中剩余的K个元素就是所求的前K个最小或者最大的元素。?
// TopK 问题求解
void PrintTopK(int* a, int n, int k)
{
// 1. 建堆--用a中前k个元素建堆
int* kminHeap = (int*)malloc(sizeof(int) * k);
assert(kminHeap);
for (int i = 0; i < k; ++i)
{
kminHeap[i] = a[i];
}
// 建小堆
for (int j = (k - 1 - 1) / 2; j >= 0; --j)
{
AdjustDown(kminHeap, k, j);
}
// 2. 将剩余n-k个元素依次与堆顶元素交换,不满则则替换
for (int i = k; i < n; ++i)
{
if (a[i] > kminHeap[0])
{
kminHeap[0] = a[i];
AdjustDown(kminHeap, k, 0);
}
}
for (int j = 0; j < k; ++j)
{
printf("%d ", kminHeap[j]);
}
printf("\n");
free(kminHeap);
}
void TestTopk()
{
int n = 10000;
int* a = (int*)malloc(sizeof(int) * n);
srand(time(0));
for (size_t i = 0; i < n; ++i)
{
a[i] = rand() % 1000000;
}
a[5] = 1000000 + 1;
a[1231] = 1000000 + 2;
a[531] = 1000000 + 3;
a[5121] = 1000000 + 4;
a[115] = 1000000 + 5;
a[2305] = 1000000 + 6;
a[99] = 1000000 + 7;
a[76] = 1000000 + 8;
a[423] = 1000000 + 9;
a[0] = 1000000 + 10;
PrintTopK(a, n, 10);
}
int main()
{
TestTopk();
return 0;
}?打印结果:![]()
?时间复杂度O(k + logk * (N - K)), 建堆 +?向下调整N - K个数
?空间复杂度O(k)
N很大但是K很小啊,空间复杂度不高且很快
2、总结?
堆排序效率极其高,时间复杂度很小;对于一个堆来说,排序数字越多,量越大,快就体现出来了,排序时,跳过1个,2个,4个,8个,……,以2的n次方指数形式增长,这就是快的关键所在。TOP-K问题,处理海量数据,内存加载不下,换个思路,建立K个数据构成的堆,让其他N - K个数据依次遍历,与堆顶元素进行比较。
