1. 图（Graph）相关概念
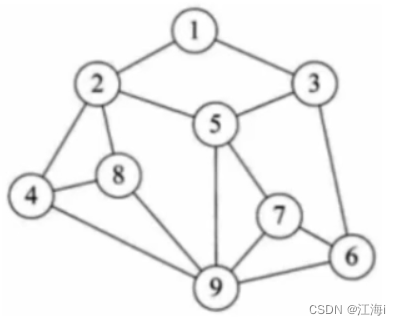
1.1 基础概念
图由**顶点(vertex)和边(edge)**组成，通常表示为
G = (V,E)。
其中：G表示一个图，V是顶点集，E是边集。
V有穷且非空。
任意两个顶点之间都可以用边来表示它们之间的关系，E可以是空的。
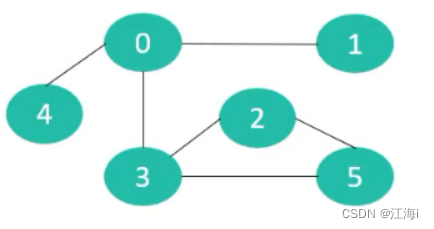
1.2 有向图（Directed Graph）
边是有明确方向的。
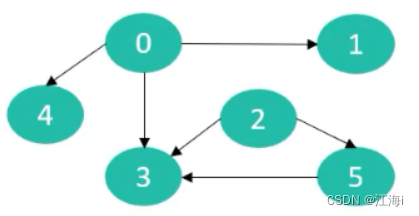
- 有向无环图（Directed Acyclic Graph，简称 DAG）
如果一个有向图，从任意顶点出发无法经过若干条边回到改顶点，就是一个有向无环图。
- 出度、入度
- 出度（Out-degree）：一个顶点的出度为
x，是指由x条边以该顶点为起点。
2. 入度（In-degree）：一个顶点的入度为x，是指由x条边以该顶点为终点。
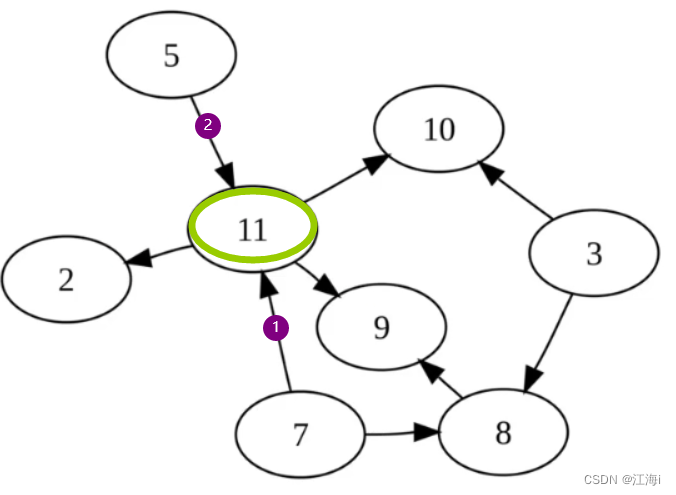
1.3 无向图（Undirected Graph）
无向图的边是无方向的。
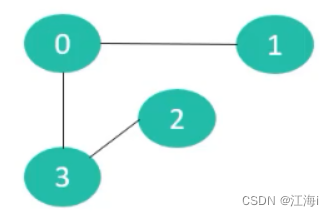
1.4 混合图（Mixed Graph）
混合图的边可能是无向的，也可能是有向的。
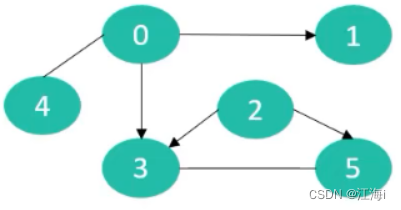
1.5 简单图、多重图
- 平行边：
- 无向图中，关联一对顶点的无向边如果多于一条，则称这些边为平行边；
- 有向图中，关联一对顶点的有向边多余一条且方向相同，则这些边为平行边。
- 多重图（Multigraph）
有平行边或者有自环的图。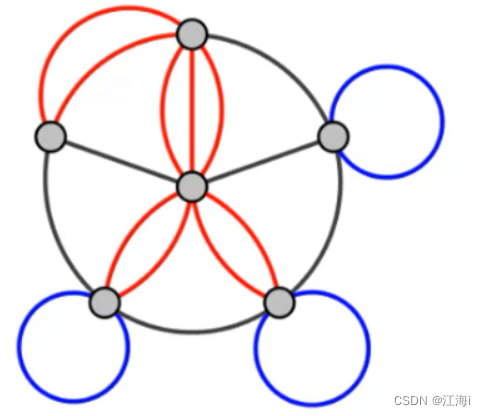
- 简单图（Simple Graph）
既没有平行边也没有自环的图。
1.6 无向完全图（Directed Complete Graph）
无向图的任意两个顶点之间都存在边。n个顶点的无向完全图有
n(n-1) / 2条边。
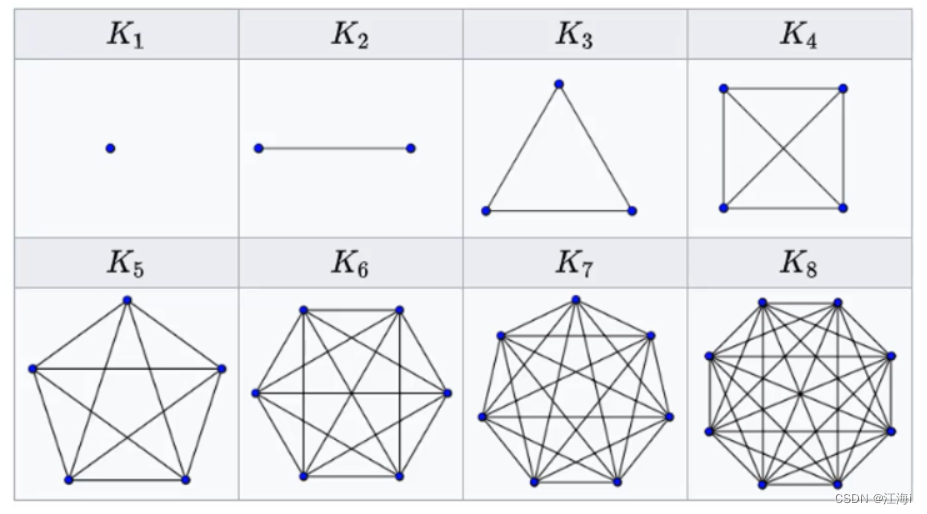
1.7 无向完全图（Undirected Complete Graph）
任意两点之间都存在方向相反的两条边。n个顶点的有向完全图有
n(n-1)条边。
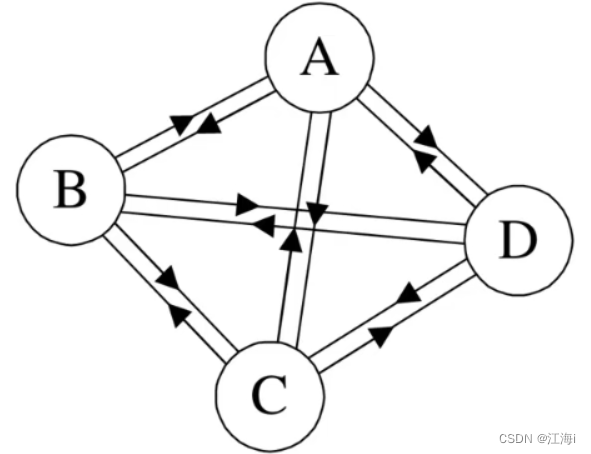
1.8 稠密图和稀疏图
- 稠密图：边的数量接近于或等于完全图。
- 稀疏图：边的数量远远小于完全图。
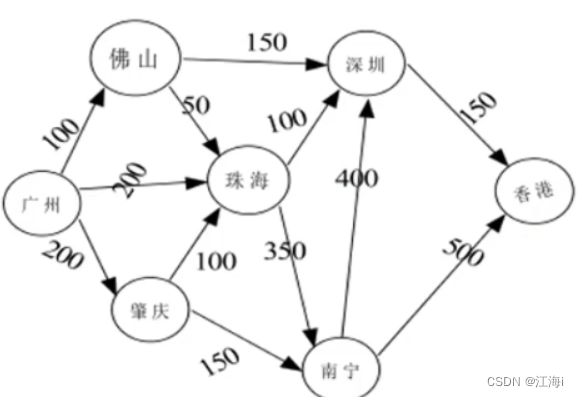
1.9 有权图（Weighted Graph）
有权图的边拥有权值。
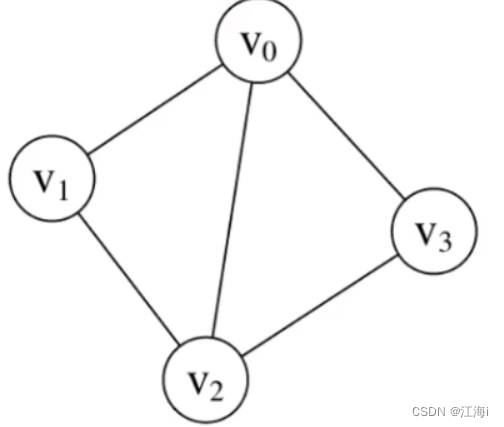
1.10 连通图（Connected Graph）
如果顶点
x和y之间存在可互相抵达的路径（直接或者间接），则称x和y是连通的。
如果无向图种任意两个顶点都是连通的，则称为连通图。
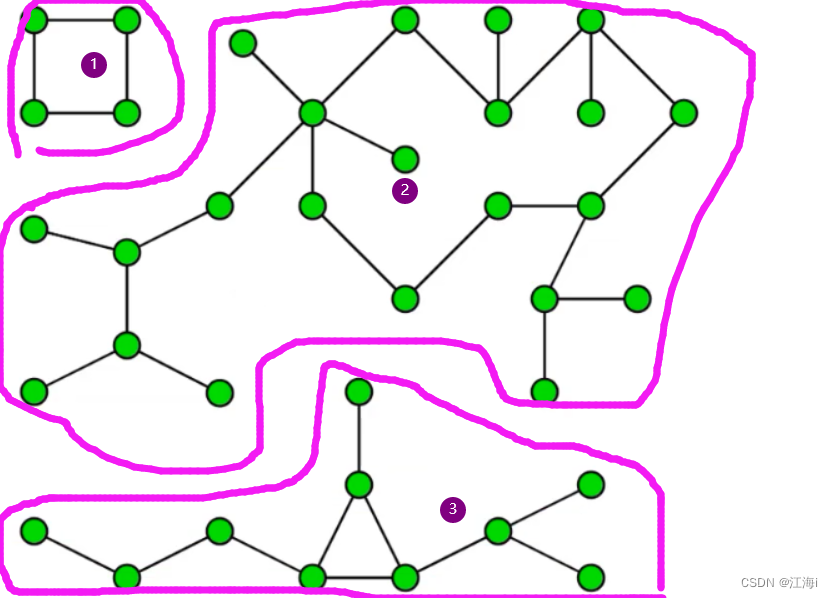
- 连通分量（Connected Component）：无向图的极大连通子图。连通图只有一个连通分量，即它本身。非连通的无向图有多个连通分量。
如：下图中有三个连通分量。
1.11 强连通图（Strongly Connected Graph）
有向图中任意两个顶点都是连通的，称为强连通图。
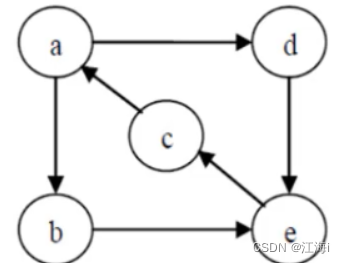
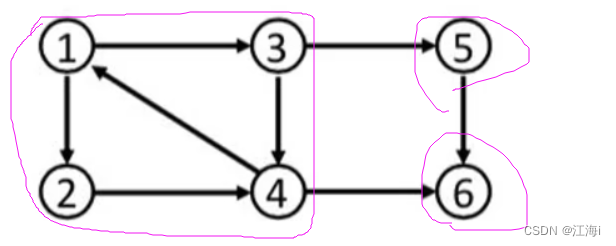
- 强连通分量（Strongly Connected Component）：有向图的极大强连通子图。连通图只有一个连通分量，即它本身。非连通的有向图有多个强连通分量。
如：下图中有三强个连通分量。
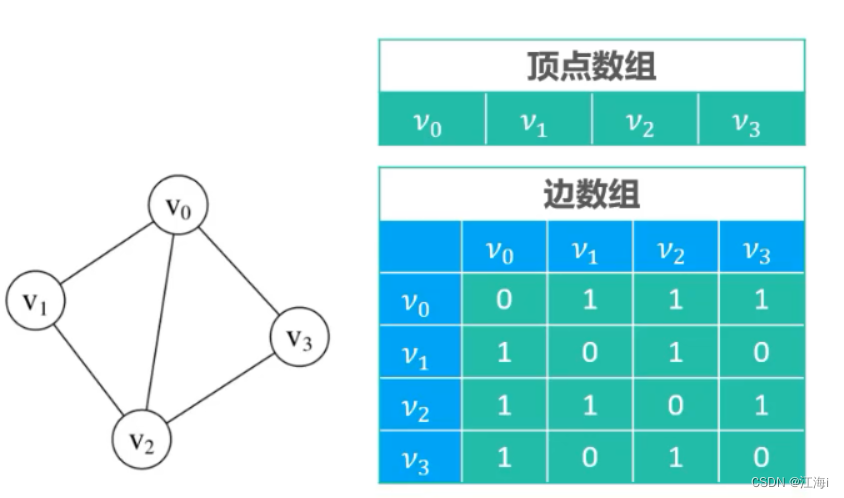
1.12 邻接矩阵（Adjacency Matrix）实现图的存储
- 存储方式：
- 一维数组存放顶点信息；
- 二维数组存放边信息。
- 无向图：二维数组中两个顶点有边用1表示，否则用0来表示。
-
有向图：二维数组中节点有出度到另一节点的边用1表示，否则用0来表示。
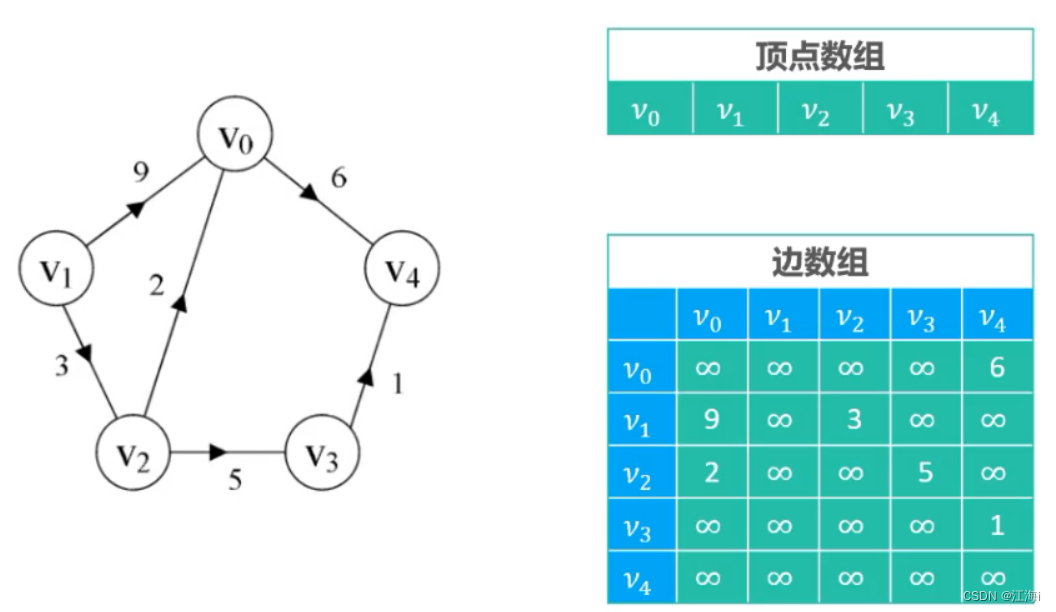
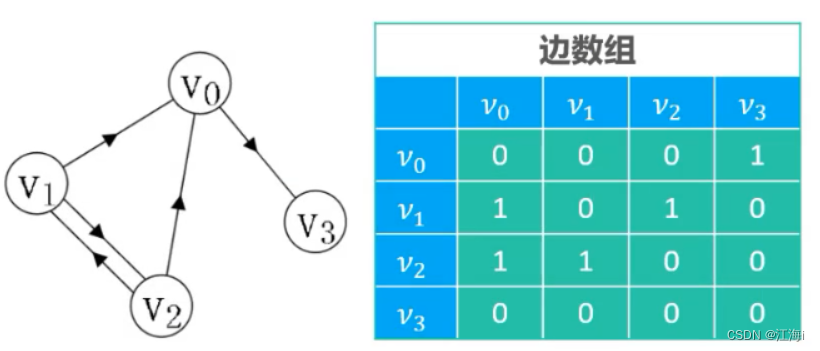- 有权图：二维数组存节点有出度到另一节点的边用权值的值表示，否则用∞来表示。
-
适合稠密图使用。
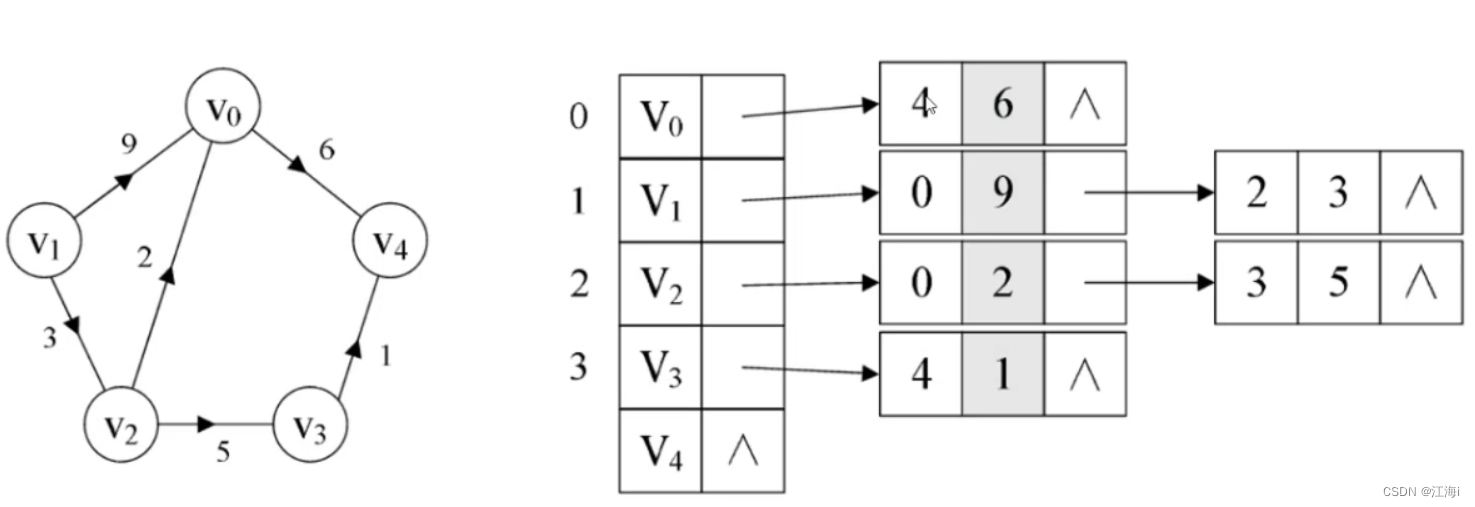
1.13 邻接表（Adjacency List）实现图的存储
- 存储方式：
- 一维数组存放顶点信息；
- 顶点作为链表的头节点，后面指向直接可达的顶点。
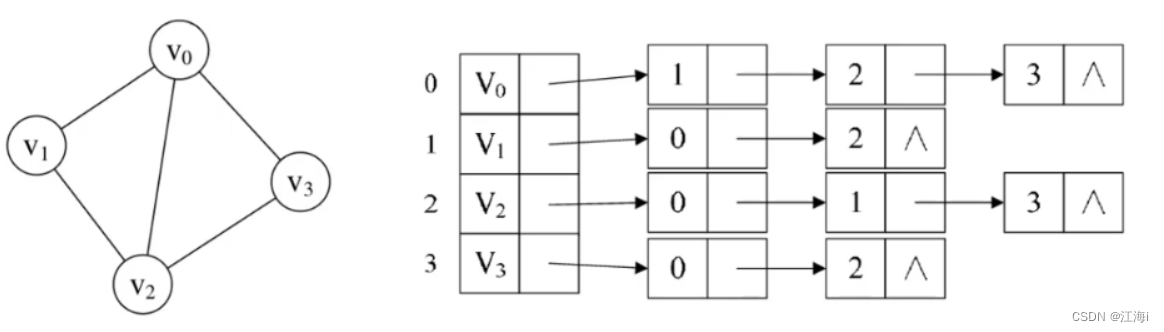
- 无向图：在链表后面存储当前顶点可以直接通往的顶点。
- 有向图：在链表后面存储当前顶点作为出度直接可达的顶点。
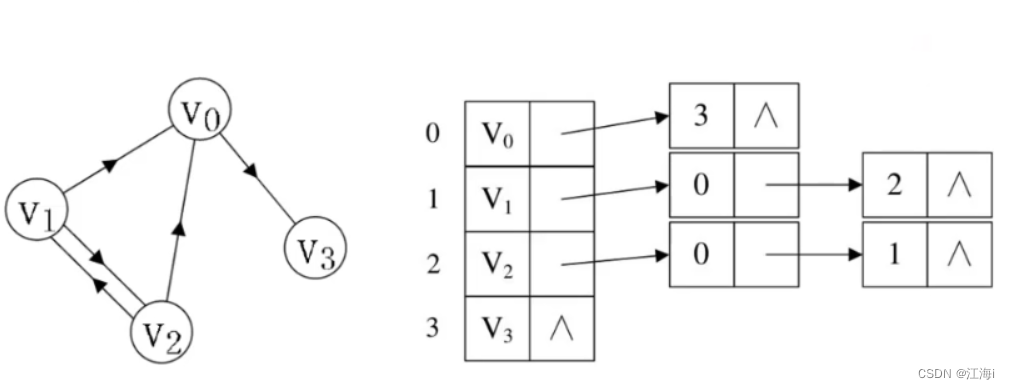
- 逆邻接表：在链表后面存储当前顶点作为入度直接可达的顶点。
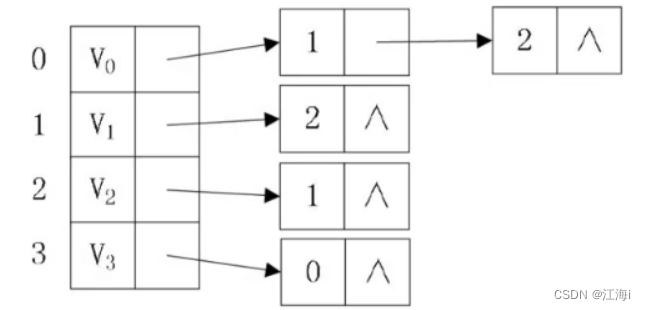
- 有权图：在链表后面存储当前顶点作为出度直接可达的顶点，并在顶点的节点类中存储权值。
2. 图的实现
2.1 接口设计
/**
* @Description 图接口
* @date 2022/5/10 20:31
*/
public interface Graph<V,E>{
/**
* 获取边的数量
* @return 边数量
*/
int edgeSize();
/**
* 获取顶点数量
* @return 顶点数量
*/
int verticesSize();
/**
* 添加一个顶点
* @param v 顶点
*/
void addVertex(V v);
/**
* 两个顶点之间添加一个边
* @param from 起点
* @param to 终点
*/
void addEdge(V from, V to);
/**
* 两个顶点之间添加一个携带权值的边
* @param from 起点
* @param to 终点
* @param weight 权值
*/
void addEdge(V from, V to, E weight);
/**
* 删除一个顶点
* @param v 顶点
*/
void removeVertex(V v);
/**
* 删除一条边
* @param from 起点
* @param to 终点
*/
void removeEdge(V from, V to);
/**
* 广度优先搜索
* @param v
*/
public abstract void bfs(V v, VertexVisitor<V> visitor);
/**
* 深度优先搜索
* @param v
*/
public abstract void dfs(V v, VertexVisitor<V> visitor);
/**
* 使用栈实现深度优先搜索
* @param v
*/
public abstract void difOfStack(V v, VertexVisitor<V> visitor);
/**
* dfs 和 bfs 遍历是外部获取值
* @param <V>
*/
public interface VertexVisitor<V> {
boolean visit(V v);
}
}
2.2 HashMap + HashSet实现图
- 节点类设计：
/**
* 顶点类
* @param <V>
* @param <E>
*/
private static class Vertex<V,E>{
// 顶点值
V v;
// 以该顶点为终点的边 入度
Set<Edge<V, E>> inEdges = new HashSet<>();
// 以该顶点为起点的边 出度
Set<Edge<V, E>> outEdges = new HashSet<>();
public Vertex(V v) {
this.v = v;
}
@Override
public boolean equals(Object o) {
// 顶点值相等就表示顶点相等
return Objects.equals(v, ((Vertex<V,E>) o).v) ;
}
@Override
public int hashCode() {
return Objects.hash(v);
}
}
/**
* 边类
* @param <V>
* @param <E>
*/
private static class Edge<V,E>{
// 起点顶点
Vertex<V, E> from;
// 终点顶点
Vertex<V, E> to;
// 权值
E weight;
@Override
public boolean equals(Object o) {
// 起点终点相同就是同一条边
return Objects.equals(from, ((Edge<V,E>) o).from) && Objects.equals(to, ((Edge<V,E>) o).to);
}
@Override
public int hashCode() {
return Objects.hash(from, to);
}
}
- 全局变量
// 存放顶点及它对应的顶点信息
private Map<V, Vertex<V, E>> vertices = new HashMap<>();
// 存放边信息
private Set<Edge<V, E>> edges = new HashSet<>();
- 边的数量 和 顶点数量
@Override
public int edgeSize() {
return edges.size();
}
@Override
public int verticesSize() {
return vertices.size();
}
- 添加顶点
@Override
public void addVertex(V v) {
if (vertices.containsKey(v)) return;
vertices.put(v,new Vertex<>(v));
}
- 添加边
@Override
public void addEdge(V from, V to) {
addEdge(from, to ,null);
}
@Override
public void addEdge(V from, V to, E weight) {
// 判断当前顶点是否存在
Vertex<V, E> fromVertex = vertices.get(from);
if (fromVertex == null){
fromVertex = new Vertex<>(from);
vertices.put(from,fromVertex);
}
Vertex<V, E> toVertex = vertices.get(to);
if (toVertex == null){
toVertex = new Vertex<>(to);
vertices.put(to,toVertex);
}
// 新建一个边
Edge<V, E> edge = new Edge<>(fromVertex, toVertex, weight);
// 删除原有的边（没有就删除不了）
if (fromVertex.outEdges.remove(edge)) {
toVertex.inEdges.remove(edge);
edges.remove(edge);
}
// 当前边是
// 1. 起点fromVertex 的出度
// 2. 终点toVertex 的入度
fromVertex.outEdges.add(edge);
toVertex.inEdges.add(edge);
edges.add(edge);
fromVertex.outEdges.add(edge);
toVertex.inEdges.add(edge);
edges.add(edge);
}
- 删除边
@Override
public void removeEdge(V from, V to) {
// 判断顶点是否存在
Vertex<V, E> fromVertex = vertices.get(from);
if (fromVertex == null) return;
Vertex<V, E> toVertex = vertices.get(to);
if (toVertex == null) return;
// 构建一条基于当前值的边
Edge<V, E> edge = new Edge<>(fromVertex,toVertex);
if (fromVertex.outEdges.remove(edge)) {
fromVertex.inEdges.remove(edge);
edges.remove(edge);
}
}
- 删除顶点
@Override
public void removeVertex(V v) {
// 直接从 map 中删除如果为空就表示不存在不需要再进行操作。
Vertex<V, E> vertex = vertices.remove(v);
if (vertex == null) return;
// 删除当前顶点时 还需要删除当前顶点作为 起点 和 终点 的边。
// 当前节点的作为出度的迭代器
Iterator<Edge<V, E>> outIterator = vertex.outEdges.iterator();
while (outIterator.hasNext()) {
// 获取作为当前顶点作为起点的边
Edge<V, E> edge = outIterator.next();
// 从边的视角来说作为 出度 即就是终点的入度
edge.to.inEdges.remove(edge);
// 迭代器中删除-从集合中删除
outIterator.remove();
// 边集合中删除
edges.remove(edge);
}
// 当前节点的作为入度的迭代器
Iterator<Edge<V, E>> inIterator = vertex.inEdges.iterator();
while (inIterator.hasNext()) {
// 获取作为当前顶点作为终点的边
Edge<V, E> edge = inIterator.next();
// 从边的视角来说作为 入度 即就是起点的出度
edge.from.outEdges.remove(edge);
// 迭代器中删除-从集合中删除
inIterator.remove();
// 边集合中删除
edges.remove(edge);
}
}
3. 广度优先搜索（Breadth First Search，简称 BFS）
又称宽度优先搜索、横向优先搜索，是一种图的遍历实现方式。
图的遍历是指从图中某一个顶点出发访问图的其余顶点，且每个顶点仅被访问一次。
二叉树的层序遍历就是一种广度优先算法。
遍历结果中的顶点没有规定的顺序。
- 无序图的遍历：以顶点
A开始，作为第一层；以顶点A直接可达的顶点B、F为第二层；依次类推G、I、C、E为第三层；H、D为第四层。
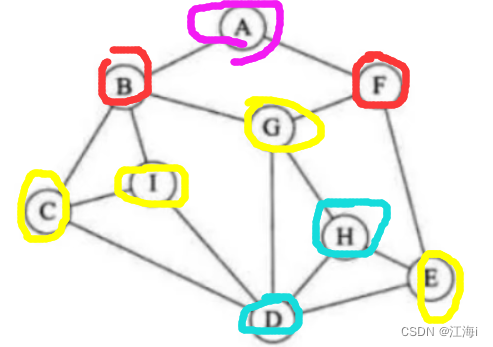
- 有序图的遍历：遍历的顺序与无序图一致，但是要遵守方向。
- 实现：与二叉树的层序遍历思路完全相同，即使用一个队列将遍历得到的顶点加入到队列中；但因为需要保证每个顶点只到达一次，需要使用
hashset来实现。
@Override
public void bfs(V v, VertexVisitor<V> visitor) {
if (visitor == null) return;
// 根据传入的顶点值 获取顶点
Vertex<V, E> beginVertex = vertices.get(v);
if (beginVertex == null) return;
// 将遍历过的节点存入到 set 中保证只遍历一次
Set<Vertex<V, E>> set = new HashSet<>();
set.add(beginVertex);
Queue<Vertex<V, E>> queue = new LinkedList<>();
queue.offer(beginVertex);
while (!queue.isEmpty()){
Vertex<V, E> vertex = queue.poll();
if (visitor.visit(vertex.v)) return;
set.add(vertex);
for (Edge<V,E> outEdge : vertex.outEdges) {
if (set.contains(outEdge.to)) continue;
queue.offer(outEdge.to);
}
}
}
4. 深度度优先搜索（Depth First Search，简称 DFS）
二叉树的前序遍历其实就是深度优先搜索的一种。
其实就是从选定的一个顶点，一直往下走，直到走不动就倒退一个顶点选择其它的方向走，走不动再倒退顶点，类推…。
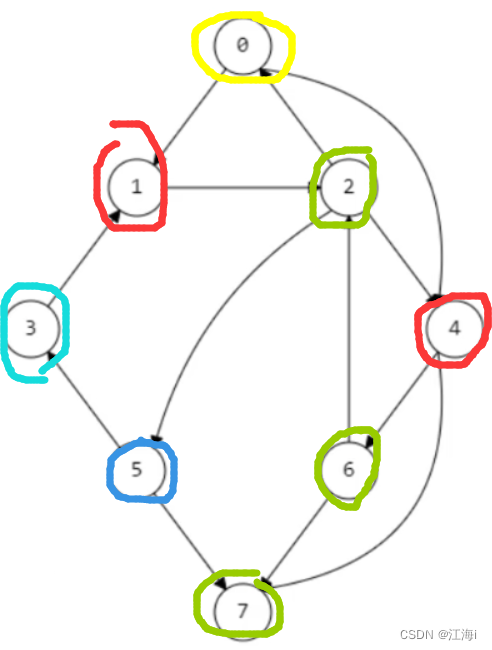
- 无序图的遍历：
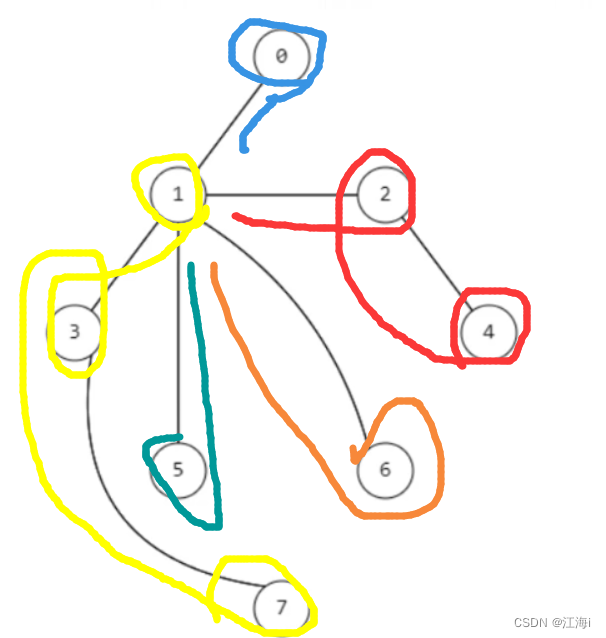
- 有序图的遍历：如下图中：先走蓝线，等到再次走到顶点
e时，无法再进行遍历，就回退，一直回退到节点e，然后选择其它方向f。
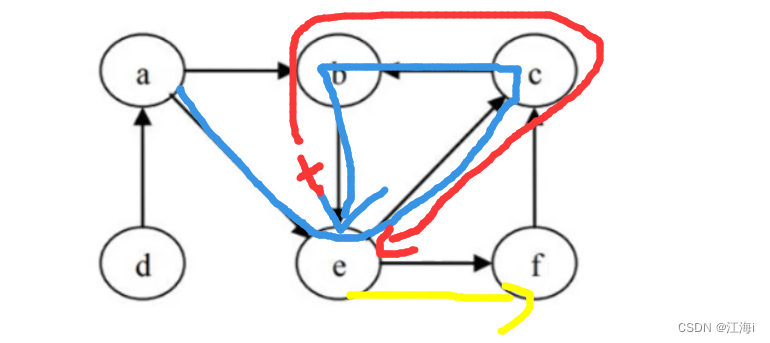
- 实现：与前序遍历思路相同，将切换到左右子节点的代码换成切换成当前顶点往外出去的线的终点的点，再附加
set保证唯一即可。
@Override
public void dfs(V v, VertexVisitor<V> visitor) {
if (visitor == null) return;
Vertex<V, E> beginVertex = vertices.get(v);
if (beginVertex == null) return;
dfs(beginVertex, new HashSet<>(), visitor);
}
private void dfs(Vertex<V, E> vertex, Set<Vertex<V,E>> set, VertexVisitor<V> visitor){
if (visitor.visit(vertex.v)) return;
set.add(vertex);
for (Edge<V,E> outEdge : vertex.outEdges) {
if (set.contains(outEdge.to)) continue;
dfs(outEdge.to, set, visitor);
}
}
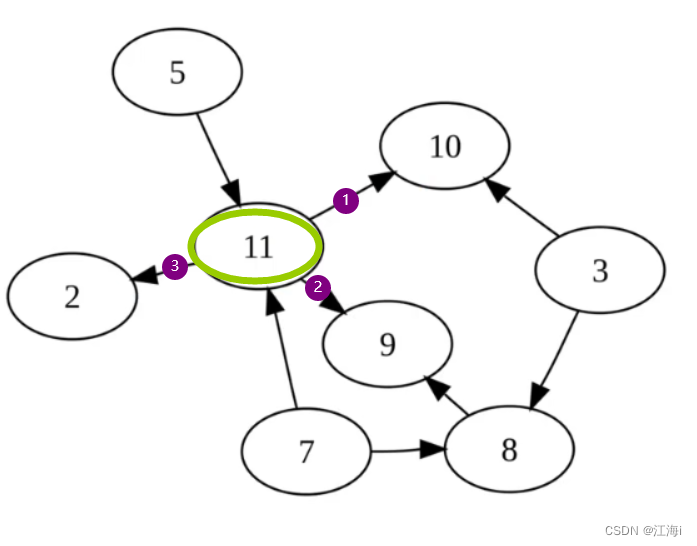
- 非递归方式，使用栈实现：
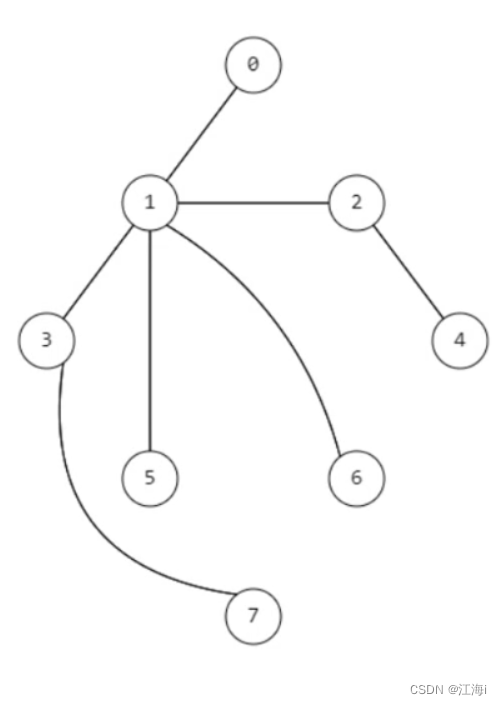
这里以顶点 1 作为开始顶点进行遍历。
- 将开始顶点入栈，并进行输出和出栈：
入栈：
出栈：
- 根据当前栈顶的顶点元素获取一条边，将改边的起点和终点按顺序加入到栈中，然后输出栈顶顶点；
break退出循环保证只访问一条边。
这里选择1，3这条边。
入栈：
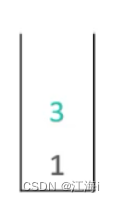
- 弹出栈顶元素，再选择一条边，将起点和终点按照顺序加入到栈中，打印此时的栈顶元素。
弹出栈顶元素：
入栈起点和终点：
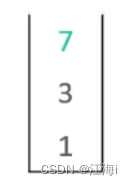
- 此时顶点7并没有其它的边可以遍历，只能弹出再弹出，直到弹出到顶点1时才能够选择其它的边，再进行入栈操作。
@Override
public void difOfStack(V v, VertexVisitor<V> visitor) {
Vertex<V, E> beginVertex = vertices.get(v);
if (beginVertex == null) return;
Set<Vertex<V, E>> set = new HashSet<>();
Stack<Vertex<V ,E>> stack = new Stack<>();
// 访问起点
stack.push(beginVertex);
set.add(beginVertex);
if (visitor.visit(beginVertex.v)) return;
while (!stack.isEmpty()){
Vertex<V, E> vertex = stack.pop();
// 遍历当前节点作为起点的边
for (Edge<V, E> edge : vertex.outEdges) {
// 访问过就跳过
if (set.contains(edge.to)) continue;
// 起点和终点都入栈
stack.push(edge.from);
stack.push(edge.to);
// 加入到set
set.add(edge.to);
if (visitor.visit(edge.to.v)) return;
break;
}
}
}
