题目1

264. 丑数 II【中等】

题解

看完才发现，和之前做的这道一样，只不过前一道是剑指offer里的，这道是力扣自己的…详细题解看链接里那道就行

状态定义：dp[i] 表示第 i 个丑数

class Solution {
    public int nthUglyNumber(int n) {
        int[] dp=new int[n];
        dp[0]=1;
        int a=0,b=0,c=0;
        for(int i=1;i<n;i++){
            int n2=dp[a]*2,n3=dp[b]*3,n5=dp[c]*5;
            dp[i]=Math.min(n2,Math.min(n3,n5));
            if(dp[i]==n2)   a++;
            if(dp[i]==n3)   b++;
            if(dp[i]==n5)  c++;
        }
        return dp[n-1];
    }
}

时间复杂度： $O (n)$

空间复杂度： $O (n)$

题目2

96. 不同的二叉搜索树【中等】

题解

动态规划

首先复习一下二叉搜索树的概念，

二叉查找树（英语：Binary Search Tree），也称为二叉搜索树、有序二叉树（Ordered Binary Tree）或排序二叉树（Sorted Binary Tree），是指一棵空树或者具有下列性质的二叉树：

若任意节点的左子树不空，则左子树上所有节点的值均小于它的根节点的值；
若任意节点的右子树不空，则右子树上所有节点的值均大于它的根节点的值；
任意节点的左、右子树也分别为二叉查找树；
没有键值相等的节点。

接着，用动态规划解这道题（不看题解真的不会啊呜呜），
在这里插入图片描述
综合两个公式可以得到卡特兰数公式，G(n)即定义的状态，求解这道题：
$G (n) = G (0) ? G (n ? 1) + G (1) ? G (n ? 2) + . . . + G (n ? 1) ? G (0)$

class Solution {
    public int numTrees(int n) {
        int[] dp=new int[n+1];
        dp[0]=dp[1]=1;
        //i为根节点
        for(int i=2;i<=n;i++){
            for(int j=1;j<=i;j++){
                dp[i]+=dp[j-1]*dp[i-j];
            }
        }
        return dp[n];
    }
}

时间复杂度： $O(n^2)$

空间复杂度： $O (n)$

卡特兰数

考研时候学的东西怕是都还给当时的自己了…

n个结点的二叉搜索树的个数为卡特兰数，直接套公式就出来了
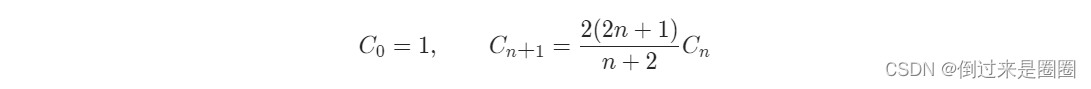
在这里插入图片描述

class Solution {
    public int numTrees(int n) {
        long C=1;//用long防止计算过程中的溢出
        for(int i=1;i<n;i++){
            C=2*(2*i+1)*C/(i+2);
        }
        return (int)C;
    }
}