LeetCode 105: 从前序与中序遍历序列构造二叉树

📖 解题思路:
(1)首先要明确两种遍历的形式:
前序遍历:也称为先根遍历,根结点 左孩子 右孩子
中序遍历:左孩子 根结点 右孩子
也就是说:通过前序遍历我们可以判断根结点,结合中序遍历我们可以判断出当前结点的左右子树。
(2)我选择创建四个数组,来不断维护前序、中序遍历的左右子树
(3)如果数组长度为零,那么直接返回空即可,也是递归的结束条件
PS: 数组长度为零与数组初始化为空有什么区别?
数组为空,代表数组的引用没有指向为数组堆中的空间,Java虚拟机没有在堆中为数组分配空间
数组长度为零,代表Java虚拟机为数组分配了空间,也有将数组的引用指向Java虚拟机在堆中分配的内存
(4)创建好根结点后,遍历数组(两个数组的长度是相同的),找到当前根结点在中序遍历中的索引,然后创建前序遍历和中序遍历的左右子树保存数组,然后再根据四个数组递归来构建左右子树
📝 Java代码部分:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode buildTree(int[] preorder, int[] inorder) {
/**
前序遍历确定根结点,中序遍历确定左右子树
*/
if(preorder.length == 0 || inorder.length == 0){
return null;
}
//创建根结点
TreeNode root = new TreeNode(preorder[0]);
//遍历inorder数组
for(int i = 0; i < preorder.length; i++){
//找到当前根结点在inorder数组中的索引
if(preorder[0] == inorder[i]){
//创建当前结点中序遍历左右子树的数组
int [] inorder_left = Arrays.copyOfRange(inorder, 0, i);
int [] inorder_right = Arrays.copyOfRange(inorder, i + 1, inorder.length);
//创建当前结点前序遍历左右子树的数组
int [] preorder_left = Arrays.copyOfRange(preorder, 1, i + 1);
int [] preorder_right = Arrays.copyOfRange(preorder, i + 1, preorder.length);
//递归创建左右子树
root.left = buildTree(preorder_left, inorder_left);
root.right = buildTree(preorder_right, inorder_right);
// break;
}
}
return root;
}
}
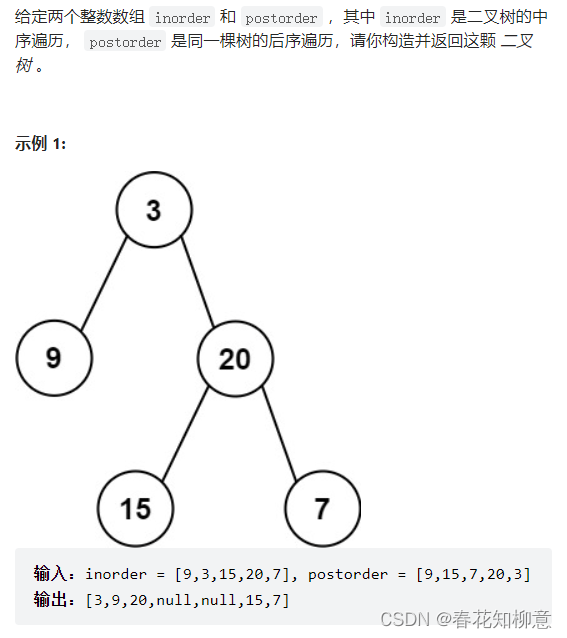
LeetCode 106: 从中序和后序遍历序列构造二叉树
?? 解题思路:
(1)与上边的属于同类型问题,解决此题的重点在于找到左右子树的结点个数,这样在创建中序和后续遍历的左右子树数组时才不会出现问题
(2)补充说明:
Arrays.copyOfRangr(int [] arr, index1, index2)
是Java中完成数组拷贝的方法,返回的是 arr数组索引从index1 - (index2 - 1)的子数组
? Java代码部分:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode buildTree(int[] inorder, int[] postorder) {
if(inorder.length == 0 || postorder.length == 0){
return null;
}
//创建根结点
TreeNode root = new TreeNode(postorder[postorder.length - 1]);
//遍历中序序列
for(int i = 0; i < inorder.length; i++){
//找到当前根结点在中序遍历中的索引
if(postorder[postorder.length - 1] == inorder[i]){
//创建中序遍历和后序遍历的左右子树
int [] inorder_left = Arrays.copyOfRange(inorder, 0, i);
int [] inorder_right = Arrays.copyOfRange(inorder, i + 1, inorder.length);
int [] postorder_left = Arrays.copyOfRange(postorder, 0, i);
int [] postorder_right = Arrays.copyOfRange(postorder, i, postorder.length - 1);
//创建左右子树
root.left = buildTree(inorder_left, postorder_left);
root.right = buildTree(inorder_right, postorder_right);
}
}
//返回根结点
return root;
}
}
