LeetCode 热题 HOT 100
前言
备战秋招,每天坚持,注意这不是题解,有的题我觉得简单的都没有注释,这相当于自己记录,督促自己的一个渠道。
题目顺序:前后交替
回顾:每一天回顾前一天没刷出来的题目,依次累加进行
提示:以下是本篇文章正文内容,下面案例可供参考
九十二、目标和
给你一个整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 ‘+’ 或 ‘-’ ,然后串联起所有整数,可以构造一个 表达式 :
例如,nums = [2, 1] ,可以在 2 之前添加 ‘+’ ,在 1 之前添加 ‘-’ ,然后串联起来得到表达式 “+2-1” 。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。

??一道01背包的转换问题,主要在于如何转换成01背包
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target) {
int sum = 0;
for (auto &a : nums) {
sum += a;
}
if ((target + sum) % 2 == 1) return 0;//注意
if (abs(target) > sum) return 0;
int bagSize = (target + sum) / 2;
vector<int> dp(bagSize + 1, 0);
dp[0] = 1;
for (int i = 0; i < nums.size(); i++) {
for (int j = bagSize; j >= nums[i]; j--) {
dp[j] += dp[j - nums[i]];
}
}
return dp[bagSize];
}
};
九十一、汉明距离
两个整数之间的 汉明距离 指的是这两个数字对应二进制位不同的位置的数目。
给你两个整数 x 和 y,计算并返回它们之间的汉明距离。

位运算经典题目
思路:两个数在某一位的二进制数不同,表示两数异或的结果在这一位为1
class Solution {
public:
int hammingDistance(int x, int y) {
//先取得有多少位不同,异或
int z = x ^ y;
int cnt = 0;
while (z) {
cnt += z & 1;//与,都是1就为1
z >>= 1;//右移
}
return cnt;
}
};
九十、找到所有数组中消失的数字
给你一个含 n 个整数的数组 nums ,其中 nums[i] 在区间 [1, n] 内。请你找出所有在 [1, n] 范围内但没有出现在 nums 中的数字,并以数组的形式返回结果。

class Solution {
public:
vector<int> findDisappearedNumbers(vector<int>& nums) {
for (int i = 0; i < nums.size(); i++) {
while (true) {
int pos = nums[i] - 1;
if (nums[i] == nums[pos]) break;
swap(nums[i], nums[pos]);
}
}
vector<int> res;
for (int i = 0; i < nums.size(); i++) {
if (nums[i] != i + 1) {
res.push_back(i + 1);
}
}
return res;
}
};
八十九、找到字符串中所有字母异位词
给定两个字符串 s 和 p,找到 s 中所有 p 的 异位词 的子串,返回这些子串的起始索引。不考虑答案输出的顺序。
异位词 指由相同字母重排列形成的字符串(包括相同的字符串)。

class Solution {
public:
vector<int> findAnagrams(string s, string p) {
vector<int> res;
int m = s.size();
int n = p.size();
vector<int> windows(26, 0);
vector<int> st(26, 0);
for (int i = 0; i < n; i++) {
st[p[i] - 'a']++;
}
int slow = 0;
for (int fast = 0; fast < m; fast++) {
windows[s[fast] - 'a']++;
if (fast >= n) {
windows[s[slow] - 'a']--;
slow++;
}
if (windows == st) {
res.push_back(slow);
}
}
return res;
}
};
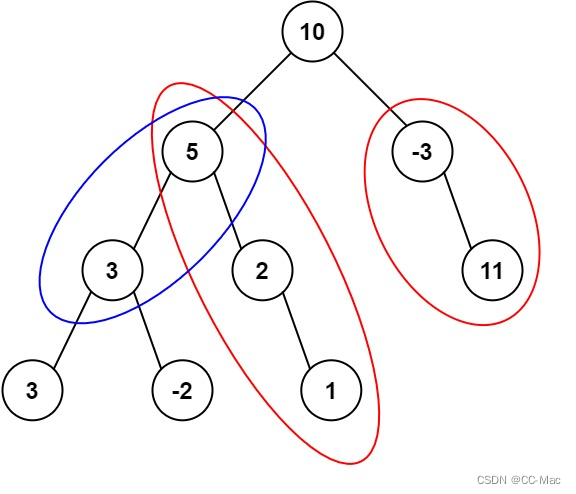
八十八、路径总和 III
给定一个二叉树的根节点 root ,和一个整数 targetSum ,求该二叉树里节点值之和等于 targetSum 的 路径 的数目。
路径 不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。

class Solution {
public:
int pathSum(TreeNode* root, int targetSum) {
int res = 0;
mp[0] = 1;
traversal(root, targetSum, 0, res);
return res;
}
void traversal(TreeNode* root, int targetSum, long long curSum, int& res) {
if (root == nullptr) return ;
curSum += root -> val;
if (mp.find(curSum - targetSum) != mp.end()) {
res += mp[curSum - targetSum];
}
mp[curSum]++;
traversal(root -> left, targetSum, curSum, res);
traversal(root -> right, targetSum, curSum, res);
mp[curSum]--;
}
private:
unordered_map<long long, int> mp;
};
总结
总之,加油
