一/二维前缀和区间和的求法
一、一维前缀和
给定一个数组A[1,2,……n],则它的前缀和数组为PrefixSum[1…n]。定义为:PrefixSum[i] = A[0]+A[1]+…+A[i-1];
例子:
A[5,6,7,8] --> PrefixSum[5,11,18,26]
PrefixSum[0] =A[0] ;
PrefixSum[1] =A[0] + A[1] ;
PrefixSum[2] =A[0] + A[1] + A[2] ;
用法:
- 可以通过前缀和求出任意区间的求和值,比如我们想求出[5,10]区间内的求和值,即s[10]-s[4]=[5,10]
思路:
对于一个给定的数组nums,使用额外开辟一个前缀和数组preSum进行预处理
int n = num.length;
int[] preSum = new int[n+1];
preSum[0]=0;
for(int i=0;i<n;i++){
preSum[i+1]=preSum[i]+num[i];
}
二、一维区间和【Leetcode 560】
给你一个整数数组 nums 和一个整数 k ,请你统计并返回该数组中和为 k 的连续子数组的个数。
示例:
输入:nums = [1,2,3], k = 3
输出:2
代码:
int subarraySum(int[] nums, int k) {
int n = nums.length;
// 构造前缀和
int[] sum = new int[n + 1];
sum[0] = 0;
for (int i = 0; i < n; i++)
sum[i + 1] = sum[i] + nums[i];
int ans = 0;
// 穷举所有子数组
for (int i = 1; i <= n; i++)
for (int j = 0; j < i; j++)
// sum of nums[j..i-1]
if (sum[i] - sum[j] == k)
ans++;
return ans;
}
缺点:时间复杂度较大,O(n*n),因为要2个for循环
解决办法:根据两数之和那题,可以使用HashMap的方式解决,即key存sum[i],如果sum[i]-k存在于map的key中,则sum[j]==sum[i]-k 或 sum[i]-sum[j]=k
public int subarraySum(int[] nums, int k) {
int length = nums.length;
Map<Integer,Integer> presum = new HashMap<>();
presum.put(0,1);
int ans = 0;
int sum_i = 0;
for(int i = 0; i < length; i++){
sum_i += nums[i];
int sum_j = sum_i - k;
if(presum.containsKey(sum_j)){
ans += presum.get(sum_j);
}
presum.put(sum_i, presum.getOrDefault(sum_i, 0) + 1);
}
return ans;
}
三、二维前缀和【力扣1314】
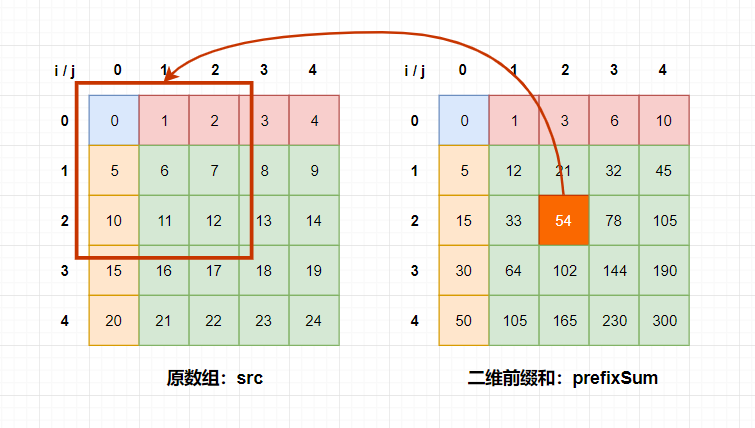
从上图中可以看出,前缀和数组里每一个位置都表示原数组当前index左上方的数字的和。
比如像图里面画的:prefixSum[3, 3] = src[0~2, 0~2]的和;
二维前缀和数组要怎么计算出来呢?
可以分为四种情况:
- i0 && j0,只有一个直接赋值即可:prefixSum[0, 0] = src[0, 0]。
- i==0,最左边的一排,图中黄色部分,prefixSum[0, j] = prefixSum[0, j-1] + src[0, j];
- j==0,最上面一排,途中红色部分,prefixSum[i, o] = prefixSum[i-1, 0] + src[i, 0];
- i!=0||j!=0,图中绿色部分,prefixSum[i][j] = prefixSum[i - 1] [j] + prefixSum[i][j - 1] + src[i][j] - prefixSum[i - 1] [j-1];
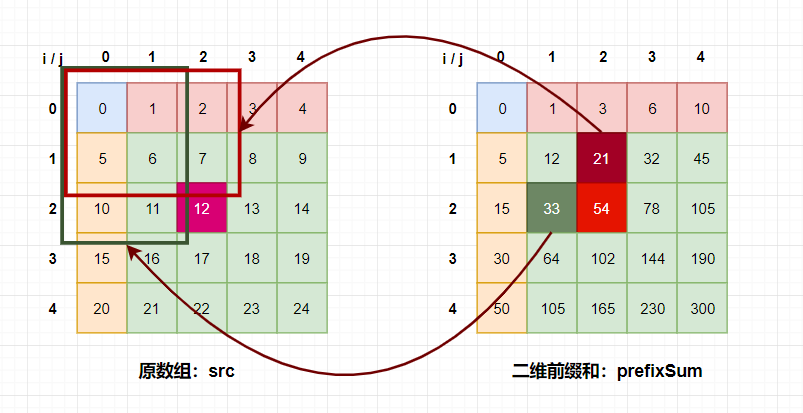
我们要得到prefixSum[2,2],我们知道应该是图一中箭头指向的区域。也就是9个方框加起来的和,也就是54。
看图二,我们可以利用prefixSum[1, 2]和prefixSum[2, 1],但是他俩的区域是重合的,如图二所示,重合的区域又恰好是prefixSum[1, 1]负责的区域,相当于加了两份,需要减掉一份。
所以prefixSum[2,2] = prefixSum[1, 2] + prefixSum[2, 1] - prefixSum[1, 1] + src[2, 2];
也就是54 = 33 + 21 -12(这个是prefixSum[1, 1]) +12(这是src[2, 2])
代码
for (int i = 0; i < src.length; i++) {
for (int j = 0; j < src[0].length; j++) {
if (i == 0 && j == 0) {//第0个,最左上角
result[i][j] = src[i][j];
} else if (i == 0) {//第一行,最顶部一行
result[i][j] = result[i][j - 1] + src[i][j];
} else if (j == 0) {//第一列,最左边一列
result[i][j] = result[i - 1][j] + src[i][j];
} else {//其他
result[i][j] =result[i-1][j] + result[i][j-1] + src[i][j] - result[i-1][j-1];
}
}
}
return result;
四、二维区间和
上面已经计算得到二维前缀和了,那么如果要计算从(i,j)到(x,y)区间的和就很容易了,可以直接根据下面的图片计算得到
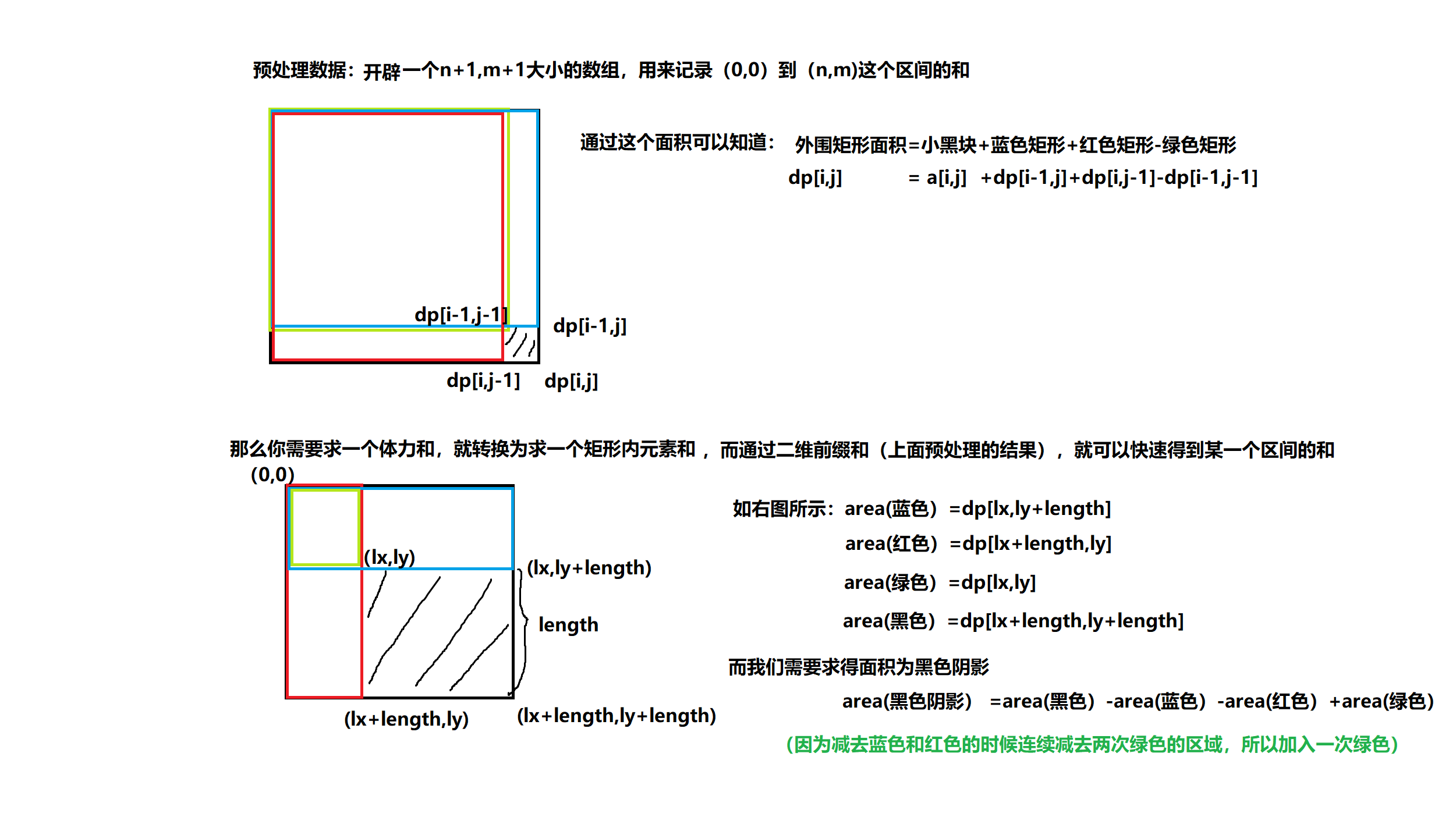
例题
给你一个 m x n 的矩阵 matrix 和一个整数 k ,找出并返回矩阵内部矩形区域的不超过 k 的最大数值和。
输入:matrix = [[1,0,1],[0,-2,3]], k = 2
输出:2
解释:蓝色边框圈出来的矩形区域 [[0, 1], [-2, 3]] 的数值和是 2,且 2 是不超过 k 的最大数字(k = 2)。
代码:
class Solution {
public int maximalSquare(char[][] matrix,int k) {
//先计算前缀和
int[][] preSum = new int[matrix.length][matrix[0].length];
for(int i=0;i<matrix.length;i++){
for(int j=0;j<matrix[0].length;j++){
if (i == 0 && j == 0) {//第0个,最左上角
preSum[i][j] = matrix[i][j];
} else if (i == 0) {//第一行,最顶部一行
preSum[i][j] = preSum[i][j - 1] + matrix[i][j];
} else if (j == 0) {//第一列,最左边一列
preSum[i][j] = preSum[i - 1][j] + matrix[i][j];
} else {//其他
preSum[i][j] = preSum[i-1][j] + preSum[i][j-1] + matrix[i][j] - preSum[i-1][j-1];
}
//上面的代码可以用三元表达式替换,当i-1<0或j-1<0时,触及边界,即前面的前缀和为0
//sum[i][j] = (i-1<0?0:sum[i-1][j]) + (j-1<0?0:sum[i][j-1]) - (i-1<0||j-1<0?0:sum[i-1][j-1]) + matrix[i][j];
}
}
//计算最大区间前缀和,即两坐标的前缀和,(i,j)到(x,y)
int max = Integer.MIN_VALUE;
for(int i=0;i<matrix.length;i++){
for(int j=0;j<matrix[0].length;j++){
for(int x=i;x<matrix.length;x++){
for(int y=j;y<matrix[0].length;y++){
int area = preSum[x][y]-
(j-1<0?0:preSum[x][j-1])-
(i-1<0?0:preSum[i][y])+
(i-1<0||j-1<0?0:preSum[i-1][j-1]);
if(area==k)return k;
if(area<k){
max = Math.max(max,area);
}
}
}
}
}
return max;
}
}
拓展:【力扣1314】
题目:
给你一个 m x n 的矩阵 mat 和一个整数 k ,请你返回一个矩阵 answer ,其中每个 answer[i] [j] 是所有满足下述条件的元素 mat[r] [c] 的和:
i - k <= r <= i + k,
j - k <= c <= j + k 且
(r, c) 在矩阵内。
示例:
输入:mat = [[1,2,3],[4,5,6],[7,8,9]], k = 1
输出:[[12,21,16],[27,45,33],[24,39,28]]
解析:
这题使用二维区间和来解决就可以了,但是注意一点,要考虑边缘问题,比如求mat[i-k] [i-k],到mat[i+k] [i+k]区间和时,需要考虑i-k<0或j-k<0,此时的值应该为0,而不是下标为0,所以边缘要+1。
代码:
class Solution {
public int[][] matrixBlockSum(int[][] mat, int k) {
int row = mat.length;
int col = mat[0].length;
int[][] preSum = new int[row+1][col+1];
int[][] res = new int[row][col];
//前缀和
for(int i=0;i<row;i++){
for(int j=0;j<col;j++){
//正常求二维前缀和的方式
// if(i==0&&j==0){
// preSum[i][j]=mat[i][j];
// }else if(i==0){
// preSum[i][j] = preSum[i][j-1]+mat[i][j];
// }else if(j==0){
// preSum[i][j] = preSum[i-1][j]+mat[i][j];
// }else{
// preSum[i][j] = preSum[i-1][j]+preSum[i][j-1]+mat[i][j]-preSum[i-1][j-1];
// }
//边缘处理
preSum[i+1][j+1] = preSum[i][j+1]+preSum[i+1][j]+mat[i][j]-preSum[i][j];
}
}
for(int i=0;i<row;i++){
for(int j=0;j<col;j++){
//左上角
int x1 = Math.max(i-k,0);
int y1 = Math.max(j-k,0);
//右下角
int x2 = Math.min(i+k,row-1);
int y2 = Math.min(j+k,col-1);
//(x1,y1)-》(x2,y2)的区间和,但不能这么算,因为i-k如果小于,因为包含区间x1和y1
//res[i][j] = preSum[x2][y2]-preSum[x1][y2]-preSum[x2][y1]+preSum[x1][y1];
//考虑边缘问题
res[i][j] = preSum[x2+1][y2+1]-preSum[x1][y2+1]-preSum[x2+1][y1]+preSum[x1][y1];
}
}
return res;
}
}
参考:https://blog.csdn.net/kuangd_1992/article/details/103466843
