《Python Machine Learning By Example》 Third Edition 第四章笔记
1 本章内容介绍
通过本章我们可以学习到:
- 决策树算法原理
- 剪枝
- 树的集成学习:聚合技术与随机森林
- GBDT及XGBoost
2 决策树原理
- 第二章我们学习的贝叶斯算法能处理数值型特征和类别型特征,因为它是计算它们的似然,而忽略特征本身的值,第三章我们学习的SVM要求特征必须是数值型的,因为算法中需要计算边界距离。本章学习的决策树也是既能处理数值型特征,也能处理类别型特征,但是比起更接近于统计学的贝叶斯,树结构的算法更加直观,树递归的过程也符合人类的决策过程。
- 我们需要自上而下构建决策树,主要包括三个部分:内部结点(训练集中基于某个特征选出的子集),决策边(某个特征的不同分支),叶子结点(最终类别),树结构如下图所示:
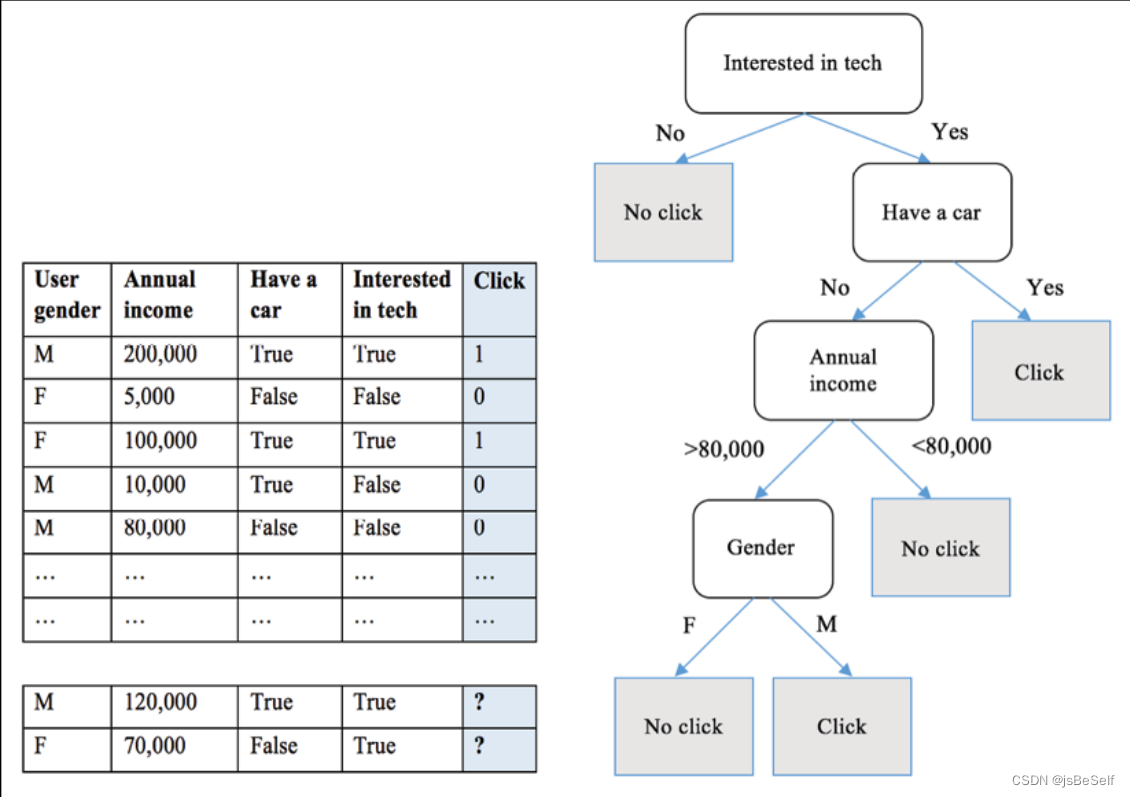
- 构建决策树的过程其实就是递归地对训练样本进行分区的过程。如果没有分区的标准,则特征空间中一共有nm 种树结构(其中n为单个特征可能取值的个数,m为特征维度),因此需要制定分区策略。这个策略就是贪心,其实每一次分区都可以看作一次贪心,选择当前样本集合中最优的特征来进行分类,直到树高度达到上限或者子集已无法再划分。但是什么样的特征算是最优特征呢?
- 根据确定最优特征的标准,可以把决策树算法分为三类:ID3(使用信息增益),C4.5(使用信息增益率),CART(使用基尼系数),下面介绍这三种决策树算法。
- ID3:首先要能体现出选择特征前后的差异,我们先引入熵的概念,它是用来表示随机变量不确定性的度量(熵越大,随机变量的不确定性就越大),若某个随机变量的概率分布为P(X=xi)=pi, 其中i = 1,2,…,n,则该随机变量的熵定义为H(X)= - ∑ pi log pi,而信息增益就是确定某个特征X之后,对类Y的信息的不确定性减小的程度,用公式表示就是g(D, A) = H(D) - H(D|A),其中H(D|A) = ∑ pi H(Di),信息增益越大,代表该特征具有更强的分类能力,所以ID3相当于使用极大似然法来选择概率模型。
- C4.5:大致与ID3相同,只是ID3有个缺点:它容易偏向于选择取值较多的特征,因为如果一个特征取值越多,每个子集就越有可能全部分类正确,那么每个子集下计算出的H就会为0,导致信息增益很大。所以C4.5将信息增益改为信息增益率,即gR(D, A) = g(D, A) / HA(D),其中HA(D) = - ∑ pi log pi。
- CART:即分类回归树算法,既可以用于分类,也可以用于回归。它由两部分组成:生成与剪枝,剪枝我们留到下一部分介绍。
1)对于回归树,包含对输入空间的一个划分及每个划分上的输出值。训练时,使用平方误差来表示预测误差,若基于平方误差最小化的准侧,可知单个分区上的输出最优值为该分区内所有实例对应真值的均值。在选择最优切分变量和切分点时,需要遍历所有输入变量,求解使得使用该切分变量后,左右子区域的平方误差和最小,并且左右分区需要求解使得该区域上均方误差最小的输出值c。
2)对于分类树,使用基尼系数来选择最优特征。基尼系数定义为 Gini(p ) = 1 - ∑ p2k,k表示第k类。基尼系数越大,样本的不确定性也越大,因此这里要求解基尼系数最小化。 - CART树是二叉树,而ID3和C4.5是多叉树。
3 决策树中的剪枝算法
- 构建树的过程是考虑局部最优,而剪枝则是考虑全局最优。因为剪枝往往要通过极小化决策树整体的损失函数来实现。前面决策树的生成部分其实也有剪枝,即预剪枝,也就是发生在决策树真正生成之前。我们可以设置,比如某个类别下的子集个数已经低于最小划分所需的样本个数,那么就生成叶子结点;或者树的高度已达上限,则停止递归。这样的方法能在一定程度上防止树结构过于复杂,也就防止了过拟合。
- 另一种剪枝发生在决策树生成之后,即后剪枝。损失函数可以定义为Cα(T) = C(T) + α|T|,其中C(T)为预测误差,|T|是树叶子结点的个数,即为模型复杂度。较大的α促使学习到较为简单的模型,较小的α促使学习到较复杂的模型。剪枝,其实就是带正则化的损失函数最小化。如果剪枝后的损失函数值小于等于剪枝前的值,则进行剪枝。(等于是因为同等损失函数下,根据奥卡姆剃刀原理,我们更愿意选择较为简单的模型)
4 树的集成学习
- 如果将bagging用到决策树算法上,就是通过重置采样,平行且独立地训练出一批树模型,然后在预测时进行投票选举,从而减小模型的方差。然而,这样的训练方法会导致各个树之间的相关性比较强,预测效果没有太大的提升。
- 为了迫使每棵树变得不相关,就引出了随机森林。树的聚合只是对训练样本随机采样,而随机森林不仅是样本随机,而且在搜索每个结点的最佳分割时,样本内的特征也只随机选取一部分来用于训练。这样就保证了更多的多样性和更好的性能。
- 随机森林的参数中,有对于单棵树的最大深度和最小分割样本数,跟前面一样是用来防止过拟合的;有对于随机森林的树的个数(通常可以设置为100,200,500)和每次搜索使用的特征数(对于一个m维的数据集,通常可以将该参数设置为根号m)。
5 拓展
- 与前面并行训练的随机森林不同,有人又提出了GBDT(Gradient Boosting Decision Tree),即梯度提升树,如下所示。这种算法的每一棵树都是建立在前一棵树的基础上,即后一棵树想要修正前一棵树的错误(后一棵树学习的目标是前一棵树与真实输出间的误差),最后再将所有的树的输出值加起来就是最终的输出值。
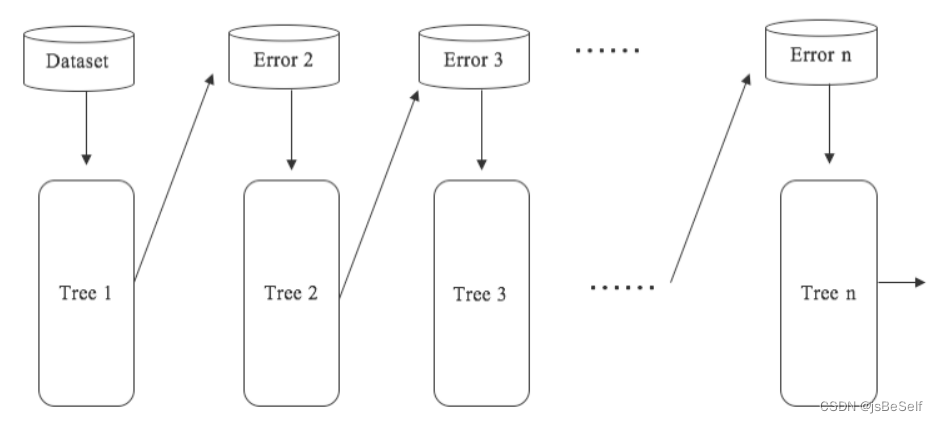
- 这种前一个模型依赖于上一个模型的方法叫做Boosting。XGBoost是GBDT的优秀版本:训练模式上与GBDT相同,而XGBoost的损失函数包含了预测项和正则项,预测项里通常是计算一阶导数来判断梯度下降的方向,而XGBoost还计算了二阶导数,进一步考虑了梯度变化的趋势,拟合更快,正则项防止过拟合。XGBoost的优点就在于提高了训练速度,决策树的速度瓶颈就在于最优特征的选择上,XGBoost将所有特征进行排序,形成一个结构,之后重复利用,提高了效率。它的缺点是:它在高维稀疏数据集上和小规模数据集上表现不是很好。
