题目描述
46.全排列:给定一个不含重复数字的数组nums,按任意顺序返回所有全排列。
47.全排列II:给定一个含重复数字的数组nums,按任意顺序返回所有不重复的全排列。
题解
46.全排列:是标准的DFS模板。对数组中的每个位置设一个visited变量,然后依次枚举每个位置,从visited为false中的数选一个填到当前位置,然后深搜下一个位置,记得深搜完毕要恢复现场。
class Solution {
public List<List<Integer>> permute(int[] nums) {
int n = nums.length;
boolean[] visited = new boolean[n];
int[] path = new int[n];
List<List<Integer>> ans = new ArrayList<>();
dfs(nums, 0, visited, path, ans);
return ans;
}
private void dfs(int[] nums, int idx, boolean[] visited, int[] path, List<List<Integer>> ans) {
if (idx == nums.length) {
// reach end
List<Integer> list = new ArrayList<>();
for (int p : path) list.add(p);
ans.add(list);
return ;
}
for (int i = 0; i < nums.length; i++) {
if (visited[i]) continue;
path[idx] = nums[i];
visited[i] = true; // 已经使用
dfs(nums, idx + 1, visited, path, ans);
visited[i] = false; //恢复现场
// path[idx] 不用恢复, 因为会在for循环的下一次迭代时被覆盖掉
}
}
}
47.全排列II:是46的升级版,关键在于如何去重。假设数组是[1,1,2],我们对第二个1进行标记,看作[1,1',2]。按照46标准的DFS做法,则会出现的重复排列有:[1,1',2]和[1',1,2],[1,2,1']和[1',2,1],[2,1,1']和[2,1',1]。我们把DFS的过程表示出来如下
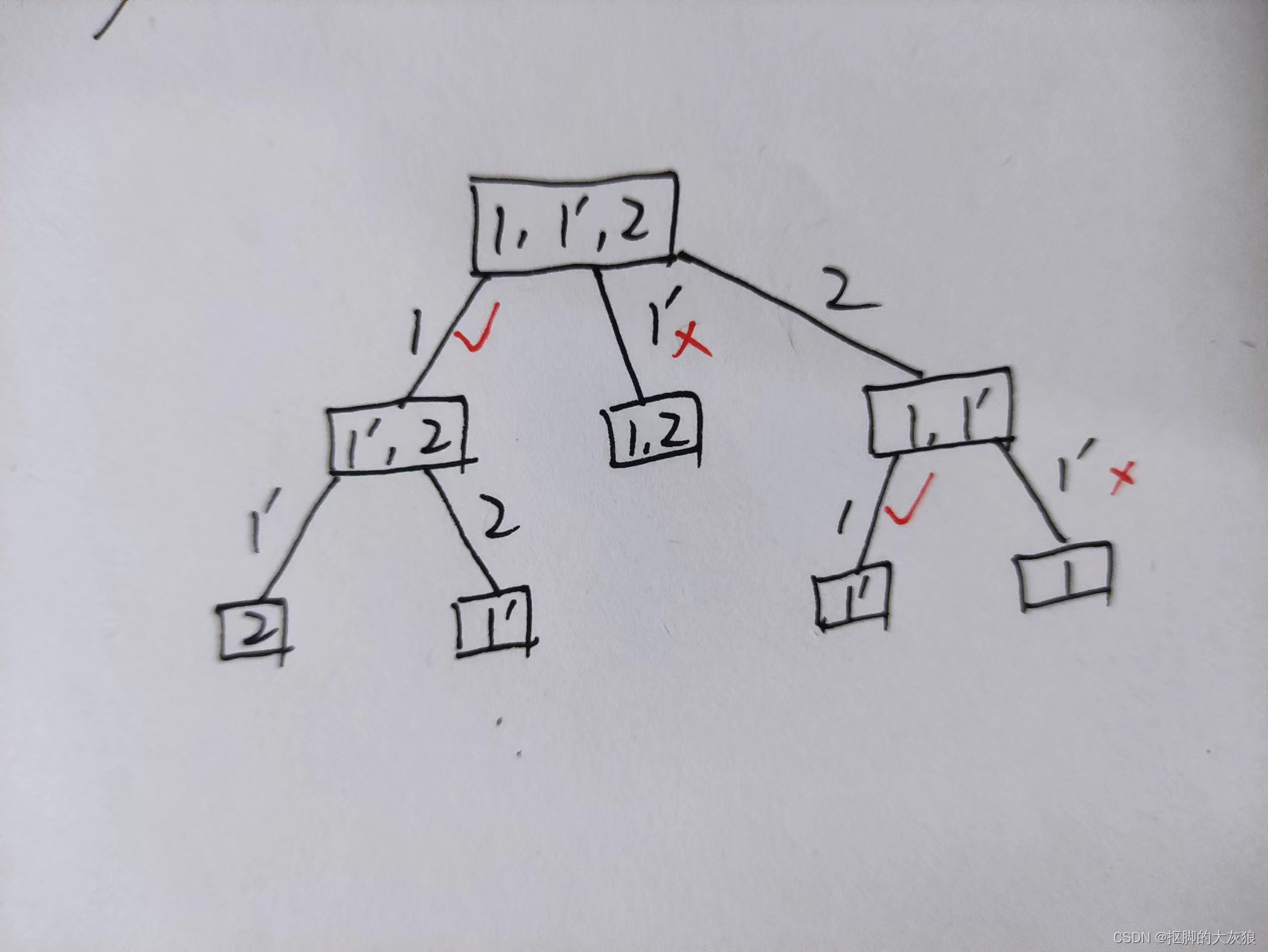
可以观察到,如何去重呢?当某一个位置,已经被相同的数字填充过了,则后续再遇到相同数字想要放到这个位置上,直接剪枝。
比如,在决定第一个位置要放什么数字时,上图中树的第二层的最左侧选择了1,则这个1的分支下面包含了所有1xx的排列,那么在这个分支走完后。尝试选择下一个放到第一个位置的数字,又遇到了1',可想这个1'的分支下面,肯定也全是1'xx的排列。由于第一个位置已经放过1这个数字了,那么1'放到第一个位置,就剪枝即可。
同样的,再看树的第二层的最右侧,第一个位置选择了2,然后第二个位置先选择了1,那么就形成了21x这样的排列;在后面尝试把1'放到第二个位置时,发现第二个位置先前已经放过1了,那么直接剪枝。
我们只需要先对数组排个序,这样,只要相同的数字,就一定是连续相邻的,我们只要保证,在尝试往某个位置放数字时,如果这个数字是重复数字,则只放第一个数,对后续的重复数字,尝试放到该位置,直接剪枝。
class Solution {
public List<List<Integer>> permuteUnique(int[] nums) {
int n = nums.length;
boolean[] visited = new boolean[n];
int[] path = new int[n];
List<List<Integer>> ans = new ArrayList<>();
Arrays.sort(nums); // 先排序
dfs(nums, 0, visited, path, ans);
return ans;
}
private void dfs(int[] nums, int idx, boolean[] visited, int[] path, List<List<Integer>> ans) {
if (idx == nums.length) {
List<Integer> list = new ArrayList<>();
for (int p : path) list.add(p);
ans.add(list);
return ;
}
for (int i = 0; i < nums.length; i++) {
// 尝试将 nums[i] 这个数字放在第 idx 个位置
// 若 nums[i] 和 前一个数 nums[i - 1]相等, 并且前一个数字还没有被访问, 则剪枝
if (visited[i] || (i > 0 && nums[i] == nums[i - 1] && !visited[i - 1])) continue;
path[idx] = nums[i];
visited[i] = true;
dfs(nums, idx + 1, visited, path, ans);
visited[i] = false; // 恢复现场
// path[idx] 同样不需要恢复, for循环的下一次迭代, 会将其覆盖
}
}
}
