文章目录
二叉树遍历的三种方法
由二叉树的递归定义可知,遍历左子树和遍历右子树可如同遍历二叉树一样“递归”进行。

写出下图二叉树的各种遍历顺序
写出下图二叉树的各种遍历顺序
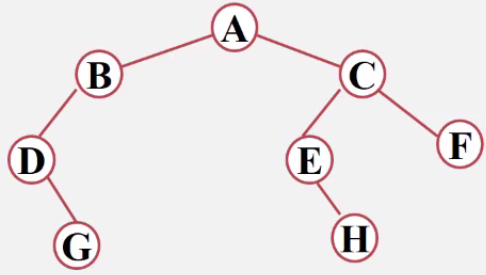
答:
先序:A B D G C E H F
中序:D G B A E H C F
后序:G D B H E F C A
性质
若二叉树中各节点的值均不相同,则二叉树结点的先序序列、中序序列和后序列都是唯一的。
由二叉树的先序序列和中序序列,或由二叉树的后序序列和中序序列可以确定唯一一棵二叉树。
已知先序中序、后序中序确定一颗二叉树
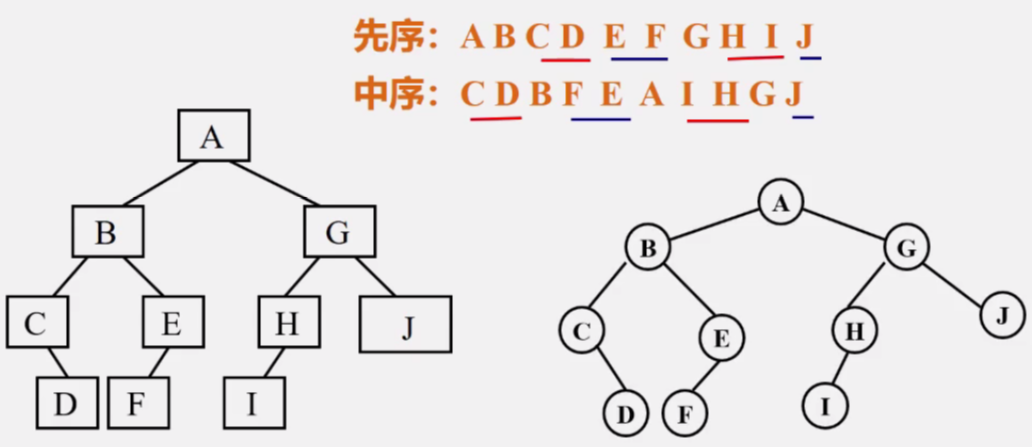
先序:A B C D E F G H I J
中序:C D B F E A I H G J
分析:由先序序列确定根;由中序序列确定左右子树。
1.由先序知根为A,则由中序知左子树为CDBFE,右子树为IHGJ。
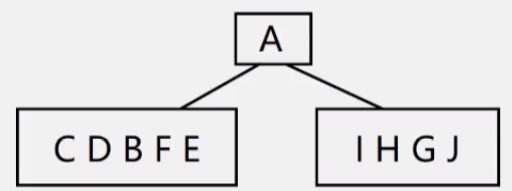
2.CDBFE和IHGJ再分别确定根。
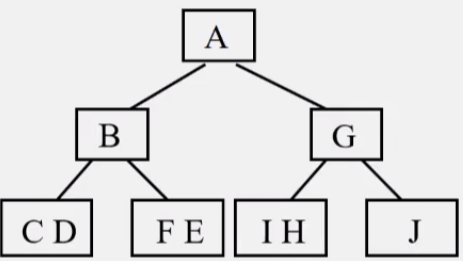
3.以此类推,得到二叉树
已知中序后序,确定一棵二叉树
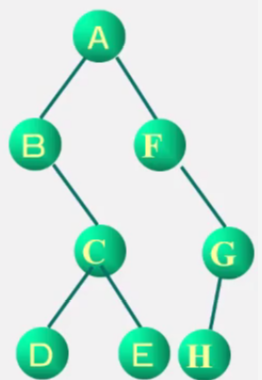
中序序列:BDCEAFHG
后序序列:DECBHGFA,请画出这棵二叉树。
提示:后序遍历,根结点必在后序序列尾部。
后序:DECBHGFA
中序:BDCEAFHG
后序:DECB 后序:DEC
中序:BDCE 中序:DCE
后序:HGF 后序:HG
中序:FHG 中序:HG
二叉树遍历递归算法
二叉树先序遍历算法
Status PreOrderTraverse(BiTree T) {
if(T == NULL) return OK; // 空二叉树
else {
visit(T); // 访问根节点,例如,输出根节点printf("%d\t", T -> data);
PreOrderTraverse(T -> lchild); // 递归遍历左子树
PreOrderTraverse(T -> rchild); // 递归遍历右子树
}
}
二叉树中序遍历算法
Status InOrderTraverse(BiTree T) {
if(T == NULL) return OK; // 空二叉树
else {
InOrderTraverse(T -> lchild); // 递归遍历左子树
visit(T); // 访问根节点
InOrderTraverse(T -> rchild); // 递归遍历右子树
}
}
二叉树后序遍历算法
Status PostOrderTraverse(BiTree T) {
if(T == NULL) return OK; // 空二叉树
else {
PostOrderTraverse(T -> lchild); // 递归遍历左子树
PostOrderTraverse(T -> rchild); // 递归遍历右子树
visit(T); // 访问根节点
}
}
遍历算法的分析
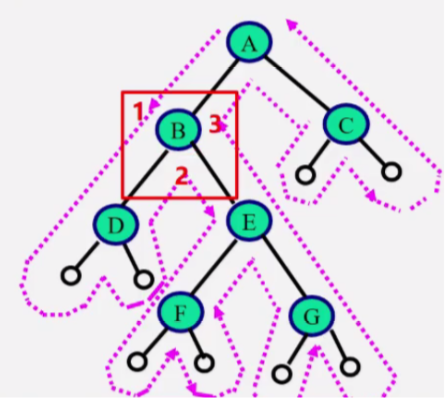
如果去掉输出语句,从递归的角度看,三种算法是完全相同的,或说这三种算法的访问路径是相同的,只是访问结点的时机不同。
从虚线的出发点到终点的路径上,每个结点经过3次。
第1次经过时访问 = 先序遍历。
第2次经过时访问 = 中序遍历。
第3次经过时访问 = 后序遍历。
遍历算法的时间效率:O(n),每个结点只访问一次。
遍历算法的空间效率:O(n),栈占用的最大辅助空间。
二叉树遍历非递归算法
中序遍历非递归算法
二叉树中序遍历的非递归算法的关键:在中序遍历过某结点的整个左子树后,如何找到该结点的根以及右子树。
基本思想:
(1)建立一个栈。
(2)根结点进栈,遍历左子树。
(3)根结点出栈,输出根结点,遍历右子树。

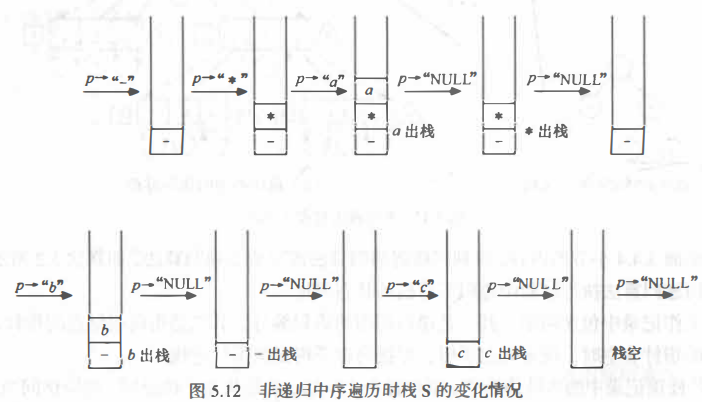
上述算法,下图所示二叉树的中序非递归遍历的栈S的变化过程如图所示:
二叉树的层次遍历
使用队列类型定义
typedef struct {
BTNode data[MaxSize]; // 存放队中元素
int front, rear; // 队头和队尾指针
} SqQueue; // 顺序循环队列类型
二叉树的层次遍历算法
void LevelOrder(BTNode *b) {
BTNode *p; SqQueue *qu;
InitQueue(qu); // 初始化队列
enQueue(qu, b); // 根结点指针进入队列
while (!QueueEmpty(qu)) { // 队不为空,则循环
deQueue(qu, p); // 出队结点p
printf("%c", p -> data);// 访问结点p
if(p -> lchild != NULL) enQueue(qu, p -> lchild);// 有左孩子时将其进队
if(p -> rchild != NULL) enQueue(qu, p -> rchild);// 有右孩子时将其进队
}
}
遍历二叉树算法的应用
先序遍历的顺序建立二叉链表
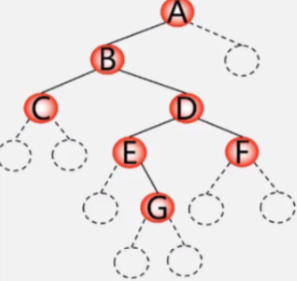
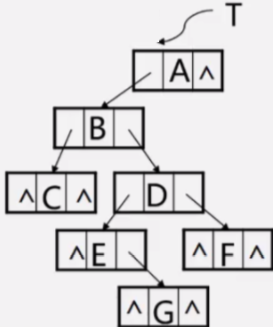
对于图示二叉树,按下列顺序读入字符:
ABC##DE#G##F###
Status CreateBiTree(BiTree &T) {
scanf(&ch); // cin >> ch;
if(ch == "#") T = NULL;
else {
if (!(T = (BiNode *)malloc(sizeof(BiTNode))))
exit(OVERFLOW); // T = new BiTNode;
T -> data = ch; // 生成根节点
CreateBiTree(T -> lchild); // 构造左子树
CreateBiTree(T -> rchild); // 构造右子树
}
return OK;
} // CreateBiTree
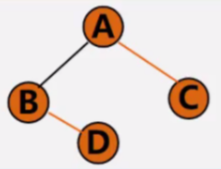
复制二叉树
如果是空树,递归结束;
否则,申请新结点空间,复制根节点。
递归复制左子树;
递归复制右子树。
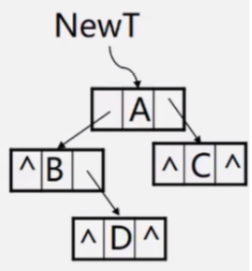
void Copy(BiTree T, BiTree &NewT)
{ // 复制一棵和T完全相同的二叉树
if(T = NULL) // 如果是空树,递归结束
{
NewT = NULL;
return;
}
else
{
NewT = new BiTNode;
NewT -> data = T -> data; // 复制根节点
Copy(T -> lchild, NewT -> lchild); // 递归复制左子树
Copy(T -> rchild, NewT -> rchild); // 递归复制右子树
} // else
}
计算二叉树的深度
如果是空树,则深度为0;
否则,递归计算左子树的深度记为m,递归计算右子树的深度记为n,二叉树的深度则为m与n的较大者加1。
int Depth(BiTree T)
{// 计算二叉树T的深度
if(T == NULL) return 0; // 如果是空树,深度为0,递归结束
else
{
m = Depth(T -> child); // 递归计算左子树的深度记为m
n = Depth(T -> rchild); // 递归计算右子树的深度记为n
if(m > n) return (m + 1); // 二叉树的深度m与n的较大者加1
else return (n + 1);
}
}
计算二叉树结点总数
如果是空树,则结点个数为0;
否则,结点个数为左子树的结点个数+右子树的结点个数再+1。
int NodeCount(BiTree T)
{// 统计二叉树T中结点的个数
if(T == NULL) return 0; // 如果是空树,则结点个数为0,递归结束
else return NodeCount(T -> lchild) + NodeCount(T -> rchild) + 1;
// 否则结点个数为左子树的结点个数+右子树的结点个数+1
}
计算二叉树叶子结点数
如果是空树,则叶子结点个数为0;
否则,为左子树的叶子结点个数+右子树的叶子结点个数。
int LeadCount(BiTree T) {
if(T == NULL) // 如果是空树返回0
return 0;
if(T -> lchild == NULL && T -> rchild == NULL)
return 1; // 如果是叶子结点返回1
else
return LeafCount(T -> lchild) + LeafCount(T -> rchild);
}
线索二叉树
如果某个结点的左孩子为空,则将空的左孩子指针域改为指向其前驱;如果某结点的右孩子为空,则将空的右孩子指针域改为指向其后继。
这种改变指向的指针称为“线索”。
加上了线索的二叉树称为线索二叉树(Threaded Binary Tree),对二叉树按某种遍历次序使其变为线索二叉树的过程叫线索化。
实例
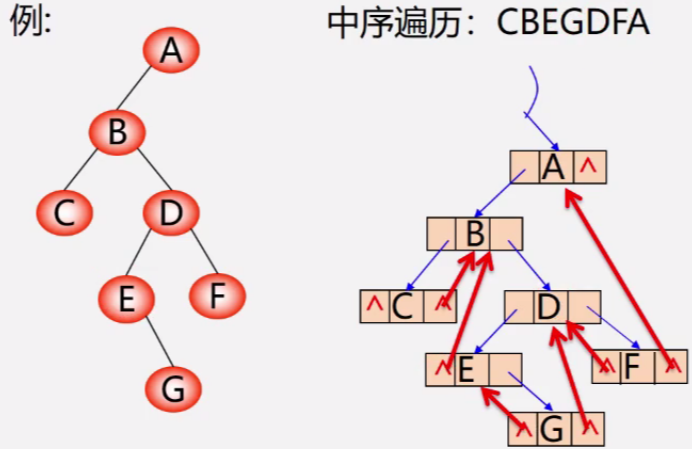
为区分lrchild和rchild指针到底是指向孩子的指针,还是指向前驱或者后继的指针,对二叉链表中每个结点增设两个标志域ltag和rtag,并约定:
ltag = 0 lchild指向该节点的左孩子
itag = 1 lchild指向该节点的前驱
rtag = 0 rchild指向该节点的右孩子
rtag = 1 rchild指向该节点的后继
这样,结点的结构为:

typedef struct BiThrNode{
int data;
int ltag, rtag;
struct BiThrNode *lchild, rchild;
} BiThrNode, *BiThrTree;
先序线索二叉树
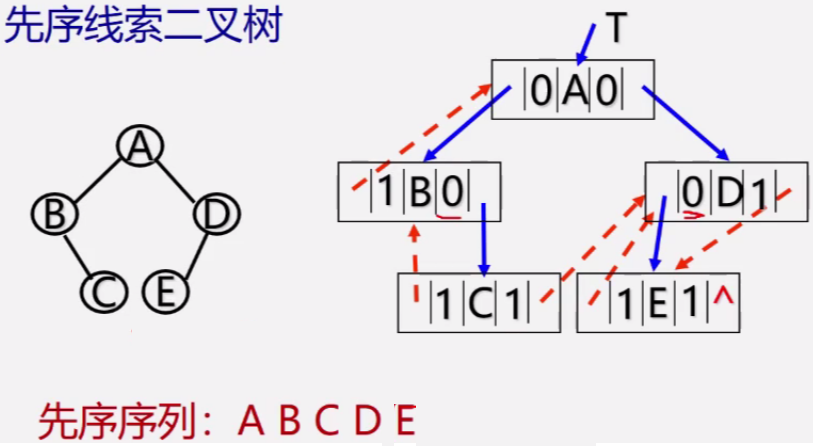
中序线索二叉树
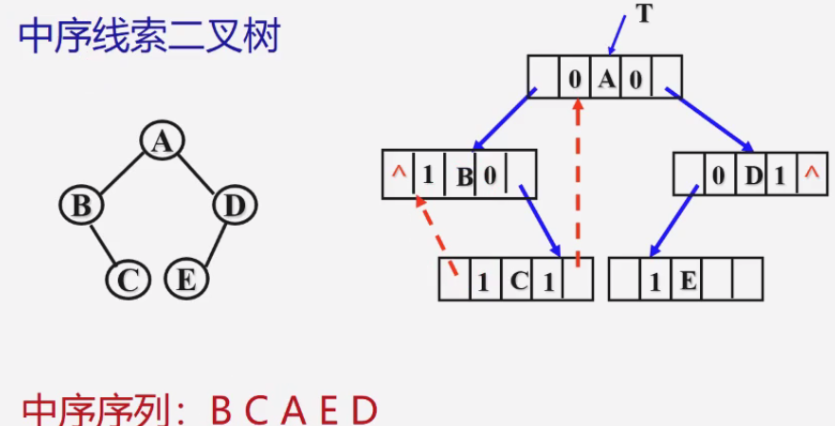
后序线索二叉树
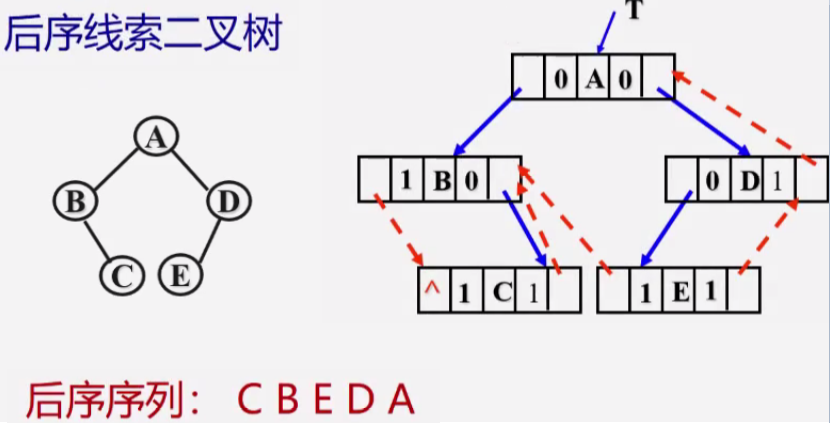
练习
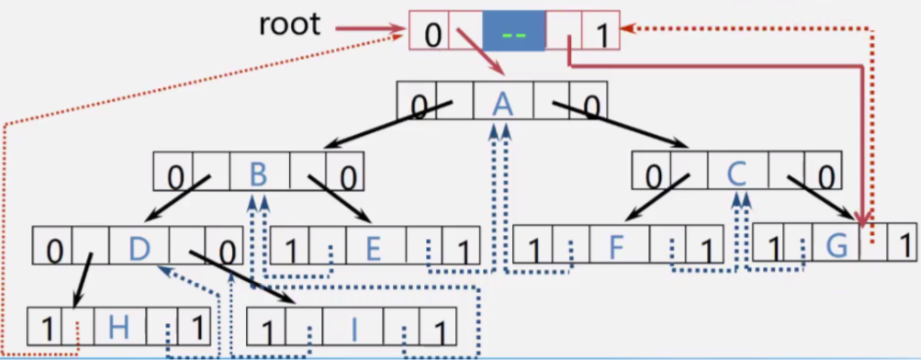
画出以下二叉树对应的中序线索二叉树。
该二叉树中序遍历结果为:H,D,I,B,E,A,F,C,G
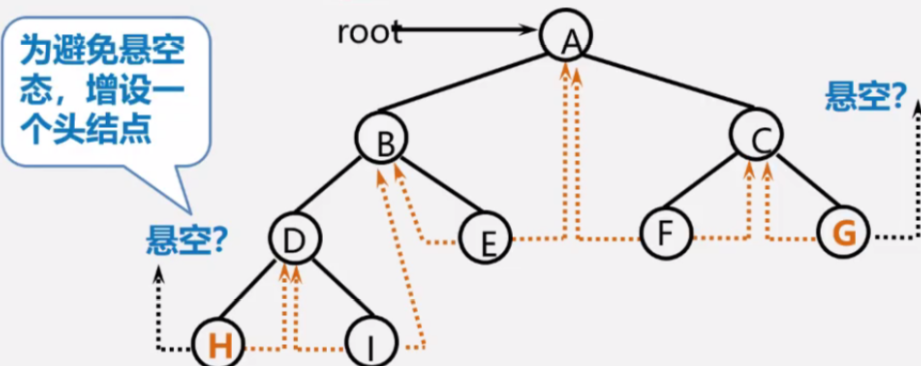
增设头结点
ltag = 0,lchild指向根节点;
rtag = 1,rchild指向遍历序列中最后一个结点。
遍历序列中第一个结点的lc域和最后一个结点的rc域都指向头结点。