题目介绍

给定很多线段，每个线段都有两个数组[start，end]，表示线段开始位置和结束位置，左右都是闭区间
规定：

线段开始和结束位置一定是整数
线段重合区域的长度必须 >= 1

返回线段最多重合区域中，包含了几条线段

思路

使用小根堆，排序
9++9

代码实现

public int MaximumSegmentCoincide() { 
	if (points.length == 0) return 0;
	Arrays.sort(points, (x, y) -> Integer.compare(x[0], y[0]));
	
	int max = 0;
	PriorityQueue<Integer> heap = new PriorityQueue<>();
	for (int i = 0; i < points.length; i++) {
	    while (!heap.isEmpty() && heap.peek() <= points[i][0]) {
	        heap.poll();    
	    }
	    heap.add(points[i][1]);
	    max = Math.max(max, heap.size());
	}
	return max;
}

LeetCode 452. 用最少数量的箭引爆气球

在这里插入图片描述

思路

那么就试一试贪心吧！局部最优：当气球出现重叠，一起射，所用弓箭最少。全局最优：把所有气球射爆所用弓箭最少。

算法确定下来了，那么如何模拟气球射爆的过程呢？是在数组中移除元素还是做标记呢？
如果真实的模拟射气球的过程，应该射一个，气球数组就remove一个元素，这样最直观，毕竟气球被射了。
但仔细思考一下就发现：如果把气球排序之后，从前到后遍历气球，被射过的气球仅仅跳过就行了，没有必要让气球数组remote气球，只要记录一下箭的数量就可以了。

以上为思考过程，已经确定下来使用贪心了，那么开始解题。
为了让气球尽可能的重叠，需要对数组进行排序。
那么按照气球起始位置排序，还是按照气球终止位置排序呢？
其实都可以！只不过对应的遍历顺序不同，我就按照气球的起始位置排序了。
既然按照起始位置排序，那么就从前向后遍历气球数组，靠左尽可能让气球重复。
从前向后遍历遇到重叠的气球了怎么办？
如果气球重叠了，重叠气球中右边边界的最小值之前的区间一定需要一个弓箭。

以题目示例： [[10,16],[2,8],[1,6],[7,12]]为例，如图：（方便起见，已经排序）

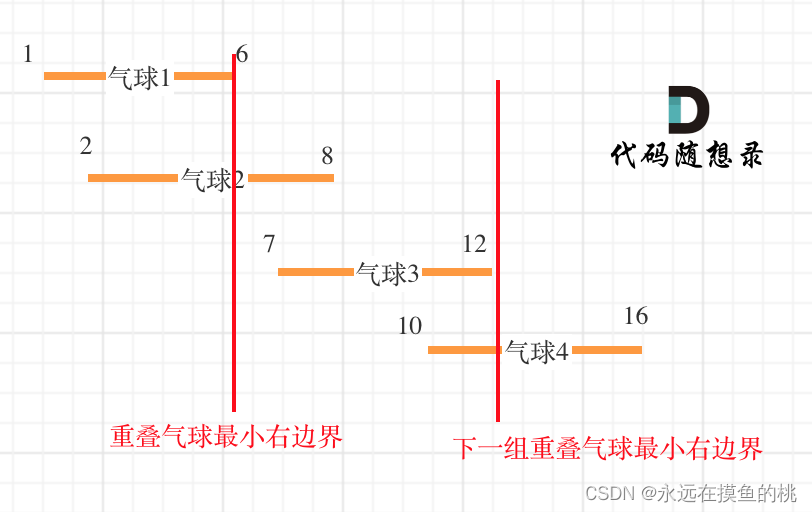
在这里插入图片描述
可以看出首先第一组重叠气球，一定是需要一个箭，气球3，的左边界大于了第一组重叠气球的最小右边界，所以再需要一支箭来射气球3了。

代码实现(java)

class Solution {
    public int findMinArrowShots(int[][] points) {
        if(points == null || points.length == 0) return 0;
        Arrays.sort(points, (x, y) -> Integer.compare(x[0], y[0]));

        // 数组不为空，就至少需要一根箭
        int count = 1;
        for(int i = 1; i < points.length; i++) {
            // 如果当前气球的左边界大于了前面的最小右边界，则说明一支箭已经不够了
            // 所以count++，开启新的下一组
            if(points[i][0] > points[i-1][1]) {
                count++;
            } else {
                // 获得当前一组气球们的最小右边界
                points[i][1] = Math.min(points[i][1], points[i-1][1]);
            }
        }
        return count;
    }
}