前言
对顶堆是数据结构堆的一种应用,属于面试必考题之一,对顶堆可以用来动态维护第k大的值,比如中位数等等。
一、例题
动态中位数
依次读入一个整数序列,每当已经读入的整数个数为奇数时,输出已读入的整数构成的序列的中位数。
输入格式
第一行输入一个整数 P,代表后面数据集的个数,接下来若干行输入各个数据集。
每个数据集的第一行首先输入一个代表数据集的编号的整数。
然后输入一个整数 M,代表数据集中包含数据的个数,M 一定为奇数,数据之间用空格隔开。
数据集的剩余行由数据集的数据构成,每行包含 10 个数据,最后一行数据量可能少于 10 个,数据之间用空格隔开。
输出格式
对于每个数据集,第一行输出两个整数,分别代表数据集的编号以及输出中位数的个数(应为数据个数加一的二分之一),数据之间用空格隔开。
数据集的剩余行由输出的中位数构成,每行包含 10 个数据,最后一行数据量可能少于 10 个,数据之间用空格隔开。
输出中不应该存在空行。
数据范围
1≤P≤1000,
1≤M≤99999,
所有 M 相加之和不超过 5×105。
输入样例:
3
1 9
1 2 3 4 5 6 7 8 9
2 9
9 8 7 6 5 4 3 2 1
3 23
23 41 13 22 -3 24 -31 -11 -8 -7
3 5 103 211 -311 -45 -67 -73 -81 -99
-33 24 56
输出样例:
1 5
1 2 3 4 5
2 5
9 8 7 6 5
3 12
23 23 22 22 13 3 5 5 3 -3
-7 -3
题目来源:acwing / 算法竞赛进阶指南
题目链接:动态中位数
思路分析:
题意很简单,就是让我们动态输出序列的中位数。如果直接暴力来做的话,必然是会超时的,而动态输出中位数,可以看成是动态输出序列的第n / 2 + 1个数,动态维护第k个数的大小,则可以用对顶堆来解决(也称为沙漏堆)。
二、算法介绍
1.对顶堆
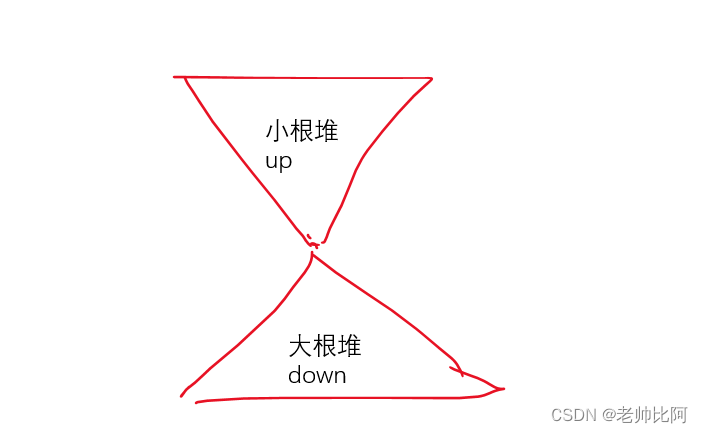
图文并茂,对顶堆的结构就是下图的样子,用一个小根堆和一个大根堆维护。
对顶堆有两个要求:
1.要求down堆的值都小于up堆的值。
2.根据题意要求维护第k大的值,down堆的数量就为 k,而up堆的数量就为n - k。(比如要求维护中位数,其实就是要求我们维护第n / 2 + 1大的值。所以down堆的数量最多大于up堆数量1个)
证明:
为什么我们这个数据结构能维护好第k大的数呢?
其实我们要维护第k大的值,可以转化成我们把比k大的值放到上面,比k小的值放在下面的问题,所以我们令大根堆的值都小于小根堆,而小根堆的最小值也大于大根堆的最大值,所以第k大的值保持在大根堆的顶部。当大根堆的数量大于小根堆数量 + k - n / 2的数时,我们就只需要更新大根堆的顶部的值,把之前的down.top加到小根堆即可.
代码
#include <cstdio>
#include <queue>
using namespace std;
int main()
{
int t;
scanf("%d",&t);
while(t -- )
{
int n,m;
scanf("%d%d",&m,&n);
printf("%d %d\n",m,(n + 1) / 2);
int cnt = 0;
priority_queue<int> down; //大根堆
priority_queue<int,vector<int> ,greater<int>> up; //小根堆
for (int i = 1; i <= n; i ++ )
{
int x;
scanf("%d",&x);
if(!down.size() || x <= down.top()) down.push(x);
else up.push(x);
if(down.size() > up.size() + 1) up.push(down.top()),down.pop();
if(up.size() > down.size()) down.push(up.top()),up.pop();
if(i % 2)
{
printf("%d ",down.top());
cnt ++;
if(cnt % 10 == 0) printf("\n");
}
}
if(cnt % 10 ) printf("\n");
}
return 0;
}

