var preorderTraversal = function (root) {

    const res=[]
    if (root) {
        res.push(root.val)
        if (root.left) res.push(...preorderTraversal(root.left))
        if (root.right) res.push(...preorderTraversal(root.right))
    }
    return res
};

2.2栈的应用场景

我们要知道什么时候用栈，这才是最重要的，所有后进先出的场景，我们都可以用栈来解决问题。

十进制转二进制

用十进制的数不断的除二取余数，然后倒过来就好了，我们就可以得到二进制了。

有效的括号

越靠后的左括号，对应的右括号越靠前，遇到左括号入栈，遇到右括号出栈，最后栈空了，就说明这个字符串合法。

下面是leetcode里的20题

 var isValid = function (s) {
        const res = []
        for (let i = 0; i < s.length; i++) {
            if (s[i] === "(" || s[i] === "{" || s[i] === "[") {
                res.push(s[i])
            }else if(s[i]==="}"){
                if(res.pop()!=="{") return false 
            } else if(s[i]===")"){
                if(res.pop()!=="(") return false 
            } else{
                if(res.pop()!=="[") return false 
            } 
            
        }
        if (res.length === 0) {
            return true
        } else {
            return false
        }

    };

函数调用堆栈

最后调用的函数是最先调用完的，js解释器是使用栈来控制函数的调用。

在vscode是支持node的调试的，我们下载一个如下插件

然后就可以打断点，然后再点击运行下面的调试就可以看到我们的callback调用栈了。

?3.队列

先进先出

3.1js中如何用队列

在js中我们没有栈这种数据结构，但是我们可以用Array来实现，用Array的shift和push实现压栈和出栈。（所有的递归都可以用栈来实现。）

3.2队列的应用场景

我们要知道什么时候用队列，这才是最重要的，所有先进先出的场景，我们都可以用栈来解决问题。

食堂排队打饭
JS异步中的任务队列

js是单线程，无法同时处理异步中的并发任务。在页面同时并发多个异步请求，也完成了，然后js该执行哪个回调函数里的?逻辑呢，如果不引入任务队列这样的数据结构，那么这个问题就处理不了

计算最近请求次数

如下例，当前时刻算，3000ms内发出的请求次数

inputs=[[],[1],[100],[3001],[3002]]

输出[null,1,2,3,4]

下面是leetcode里的933题

var RecentCounter = function() {
    this.q=[]
};

/** 
 * @param {number} t
 * @return {number}
 */
RecentCounter.prototype.ping = function(t) {
    this.q.push(t)
    while(this.q[0]<t-3000){
        this.q.shift()
    }
    return  this.q.length
};

/**
 * Your RecentCounter object will be instantiated and called as such:
 * var obj = new RecentCounter()
 * var param_1 = obj.ping(t)
 */

3.3事件循环和任务队列

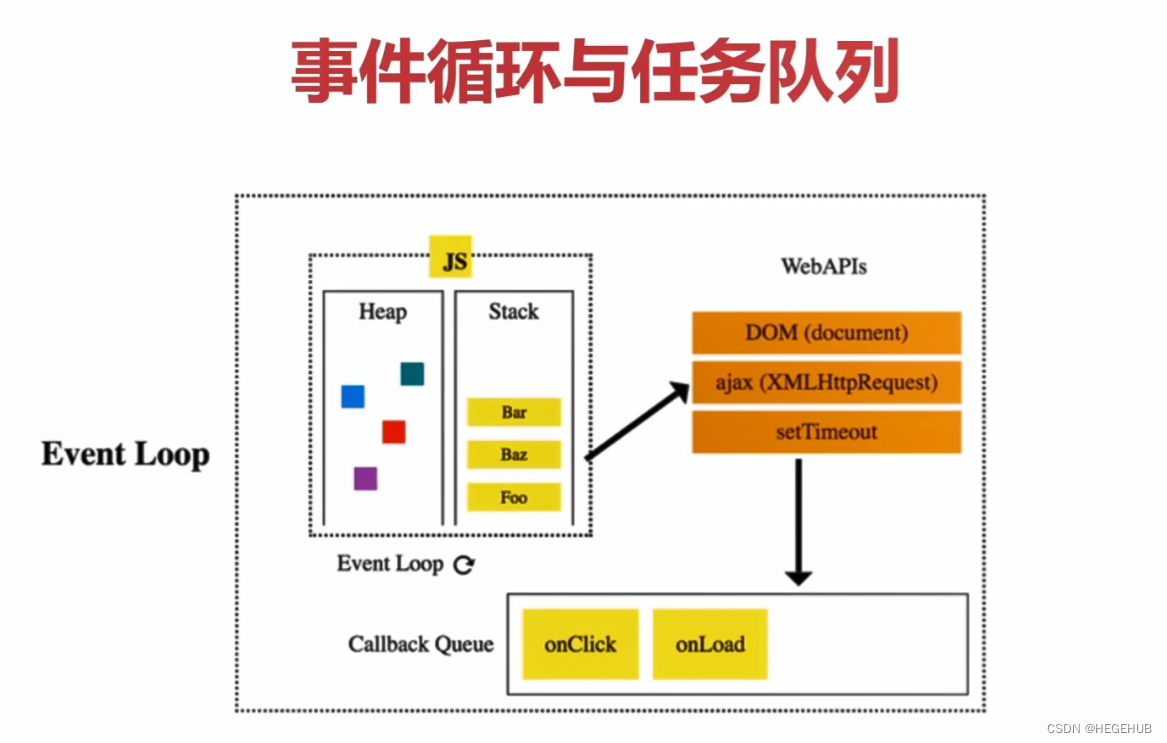
事件循环：一段js代码刚执行的时候会有一个匿名的主事件会被放在任务队列里面，js引擎会去任务队列里面取一个事件来执行，因为js引擎是单线程的所以js引擎只能处理一个事件，在执行这个事件的过程中，如果有异步任务的时候，js引擎就把任务交给外部的API去执行，然后js引擎就不管了，外部API执行异步任务结束的时候，会将回调函数放入任务队列里面，然后任务队列前面的事件执行完了，那么这个新放入的回调函数就会放入js引擎里面执行，如果新放入的回调函数里面还有异步任务，那么就继续执行做这个循环。

setTimeout（（）=>console.log(0),0）
console.log(1)

打印顺序1和0

4.链表

多个元素组成的列表
元素存储不连续，用next指针连在一起
链表增删非首尾元素的时候比数组方便，不需要大量移动元素

4.1js中如何用链表

在js中我们没有链表这种数据结构，但是我们可以用Object来实现这种数据结构。可以对用Object来实现链表的增删以及遍历。

//创建链表
const a={val:"a"}
const b={val:"b"}
const c={val:"c"}
const d={val:"d"}
a.next=b
b.next=c
c.next=d

// 遍历列表
let p=a
while(p){
    console.log(p.val)
    p=p.next
}
// 插入节点在c节点的后面
const e={val:'e'}
c.next=e
e.next=d

// 删除e节点
c.next=d

下面是leetcode里的237题

var deleteNode = function(node) {
        node.val=node.next.val
        node.next=node.next.next
};

下面是leetcode里的206题

var reverseList = function (head) {
    let p1 = null
    let p2 = head
    while (p2) {
        temp = p2.next
        p2.next = p1
        p1=p2
        p2 = temp
    }
    return p1
};

下面是leetcode里的2题

var addTwoNumbers = function(l1, l2) {
    const l3=new ListNode(0)
    let p3=l3
    let p2=l2
    let p1=l1
    let carry=0
    while(p1||p2){
        const v1=p1?p1.val:0
        const v2=p2?p2.val:0
        const val=v1+v2+carry
        carry=Math.floor(val/10)
        p3.next=new ListNode(val%10)
        if(p1) p1=p1.next
        if(p2) p2=p2.next
        p3=p3.next
    }
    if(carry){
        p3.next=new ListNode(carry)
    }
    return l3.next
};

下面是leetcode里的83题

var deleteDuplicates = function (head) {
    let p1 = head
    while (p1 && p1.next) {
        if (p1.val === p1.next.val) {
                p1.next = p1.next.next
        } else {
            p1 = p1.next
        }
    }
    return head
};

下面是leetcode里的141题

var hasCycle = function (head) {
    let p1 = head
    let p2 = head
    while (p1 && p2 && p2.next) {
        p1 = p1.next
        p2 = p2.next.next
        if (p1 === p2) {
            return true
        }
    }
    return false
};

?4.2js中的原型链和链表

其实js中的原型链的本质就是一个链表
原型链上的节点是各种原型对象，Function.prototype,Object.prototype
原型链通过__proto__属性连接各种原型对象

obj->Object.prototype->null

func->Function.prototype->Object.prototype->null

array->Array.prototype->Object.prototype->null

如果A沿着原型链能找到B.prototype，那么A?instanceof?B为true。
1. 相当于func即是Function的实例，也是Object的实例
2. 相当于array即是Array的实例，也是Object的实例
如果在A对象上没有找到x属性，那么会沿着原型链找x属性。

面试题：简述instanceof的原理，并用代码实现

解法：遍历A的原型链，如果找到B.prototype,返回true，否则返回false

let obj={}
const instanceOf=(A,B)=>{
    let p1=A
    while(p1){
        p1=p1.__proto__
        if(p1===B.prototype){
            return true
        }
    }
    return false
}
console.log(instanceOf(obj,Object))//true

?4.3js中使用链表指针获取JSON的节点值

const json = {
    a: { b: { c: 1 } },
    d: { e: 1 }
}
const path = ["a", "b", "c"]
let p2 = json
path.forEach(k => {
    p2 = p2[k]
})

5.集合

一种无序且唯一的数据结构。

栈是先进后出，队列先进先出，链表可以用next访问，所以是有序的。

而且栈队列链表的值不是唯一的，而集合的值是唯一的

5.1js中如何用集合

在js中我们有集合，名为Set

5.2集合的应用场景

集合的常用操作，去重，判断某元素是否在集合中，求交集等等

    // 数组去重
    let arr=[1,2,3,4,2,4]
    const arr1=[...new Set(arr)]
    console.log(arr1)
    // 判断元素是否在集合中
    const set=new Set([2,4,6])
    console.log(set.has(2))//true
    // 求交集
    const set1=new Set([2,6,1,8])
    const set2=new Set([...set].filter(item=>set1.has(item)))
    console.log(set2)

下面是leetcode里的349题

var intersection = function(nums1, nums2) {
    return [...new Set(nums1)].filter(item=>nums2.includes(item))
};

5.3前端与集合

Set操作

使用Set对象：new，add，delete，has，size

迭代Set对象：多种迭代方法，Set与Array互换，求交集/差集

    let mySet=new Set()
    mySet.add(2)
    mySet.add(3)
    mySet.add(2)//没用，添加重复的值
    mySet.add('2')
    mySet.add({name:"ct"})
    mySet.add({name:"ct"})//两个对象看起来一样，但是内存地址值不一样

    console.log(mySet.has(2))//true
    console.log(mySet.has('2'))//true

    mySet.delete('2')
    console.log(mySet)
    console.log(mySet.size)//4

    // 迭代Set对象
    // for of
    for (const item of mySet) {
        console.log(item)
    }
    for (const item of mySet.keys()) {
        console.log(item)
    }
    for (const item of mySet.values()) {
        console.log(item)
    }
    // Set这个结构的key和value是一样的
    for (const [key,value] of mySet.entries()) {
        console.log(key,value)
    }

    // Set转为Array
    const myArr=Array.from(mySet)
    const myArr1=[...mySet]
    console.log(myArr,myArr1)
    // Array转为Set
    const mySet2=new Set([1,2,3])
    console.log(mySet2,mySet)


    // 求Set的交集和差集
    const intersection=new Set([...mySet].filter(x=>mySet2.has(x)))
    console.log(intersection)
    const difference=new Set([...mySet].filter(x=>!mySet2.has(x)))
    console.log(difference)

6.字典

与集合类似，字典也是一种存储唯一值的数据结构，但是它是以键值对的形式来存储的。

6.1js中如何用字典

在js中我们有字典，名为Map

字典的常用操作：键值对的增删改查

6.2js中字典的增删改查

const m=new Map()

    // 增
    m.set('a',"aaa")
    m.set('b',"bbb")
    console.log(m)
    // 删
    m.delete("a")
    console.log(m)
    // 改
    m.set('b',"bbwwaa")
    console.log(m)
    // 查
    console.log(m.get("b"))
    // 删,这个删是把所有的都删完
    m.clear()
    console.log(m)

下面是leetcode里的349题（前面的解法是用Set做的）

var intersection = function(nums1, nums2) {
    const map=new Map()
    nums1.forEach(n=>{
        map.set(n,true)
    })
    const res=[]
    nums2.forEach(n=>{
        if(map.get(n)){
            res.push(n)
            map.delete(n)
        }
    })
    return res
};

下面是leetcode里的20题（前面的解法使用栈来做的）

var isValid = function (s) {
    const res = []
    const map = new Map()
    map.set("{", "}")
    map.set("(", ")")
    map.set("[", "]")
    for (let i = 0; i < s.length; i++) {
        const c = s[i]
        if (map.has(c)) {
            res.push(c)
        } else {
            const t = res[res.length - 1]
            if (map.get(t) === c) {
                res.pop()
            } else {
                return false
            }
        }
    }
    return res.length === 0
};

下面是leetcode里的1题

var twoSum = function (nums, target) {
    const map = new Map()
    for (let i = 0; i < nums.length; i++) {
        const n = nums[i]
        const n2 = target - n
        if(map.has(n2)){
            return [map.get(n2),i]
        }else{
            map.set(n,i)
        }
    }
};

下面是leetcode里的3题

var lengthOfLongestSubstring = function (s) {
    let l = 0
    let res = 0
    const map = new Map()
    for (let r = 0; r < s.length; r++) {
        if(map.has(s[r])&&map.get(s[r])>=l){
            l=map.get(s[r])+1
        }
        res = Math.max(res, r - l + 1)
        map.set(s[r],r)
    }
    return res
};

下面是leetcode里的76题(困难)?

var minWindow = function(s, t) {
    // 找出所有包含t的子串，返回长度最小的子串
    let l=0
    let r=0
    const need=new Map()
    for(let c of t){
        need.set(c,need.has(c)?need.get(c)+1:1)
    }
    let needType=need.size
    let res=""
    while(r<s.length){
        const c=s[r]
        if(need.has(c)){
            need.set(c,need.get(c)-1)
            if(need.get(c)===0) needType-=1
        }
        while(needType===0){
            const newRes=s.substring(l,r+1)
            if(!res||newRes.length<res.length) res=newRes
            const c2=s[l]
            if(need.has(c2)){
                need.set(c2,need.get(c2)+1)
                if(need.get(c2)===1) needType+=1
            }
            l+=1
        }
        r++
    }
    return res
};

7.树

一种分层数据的抽象模型

7.1js中如何用树

在js中我们没有树，但是可以用Object和Array构建树

前端工作中常见的树包括：DOM树，级联选择，树形控件?

{
    value:"123",
    label:"nihao",
    children:[
        {
            value:"123",
            label:"nihao",
            children:[]
        }
    ]
}

7.2什么是树的深度/广度优先遍历

深度优先遍历：尽可能深的搜索树的分支。相当于正常的看书，看完一章和一章的内容再看下一章。

先访问根节点
对根节点的children挨个进行深度优先遍历

广度优先遍历：先访问离根节点最近的节点。相当于先看目录，然后再看目录下面的具体内容。

新建一个队列，把根节点入队。
把队头出队并访问。
把对头的children挨个入队。
重复第二三步，直到队列为空。

    const tree = {
        val: "a",
        children: [
            {
                val: "b",
                children: [
                    {
                        val: "d",
                        children: []
                    },
                    {
                        val: "e",
                        children: []
                    },
                ]
            },
            {
                val: "c",
                children: [
                    {
                        val: "f",
                        children: []
                    }, {
                        val: "g",
                        children: []
                    },
                ]
            },
        ]
    }
    // 深度优先遍历
    const dfs=(root)=>{
        console.log(root.val)
        root.children.forEach(child => {
            dfs(child)
        });
    }
    dfs(tree)
    // 广度优先遍历
    const bfs=(root)=>{
        const q=[root]
        while(q.length>0){
            const n=q.shift()
            console.log(n.val)
            n.children.forEach(child=>{
                q.push(child)
            })
        }
    }
    bfs(tree)

7.3二叉树的先/中/后序遍历（递归版）

先中后的顺序是针对根节点的访问顺序的，中序遍历和后序遍历就调整一下访问根节点的顺序就可以了。

下面以先序遍历为例子。

访问根节点
对根节点的左子树进行先序遍历
对根节点的右子树进行先序遍历

    const bt = {
        val: 1,
        left: {
            val: 2,
            left: {
                val: 4,
                left: null,
                right: null
            },
            right: {
                val: 5,
                left: null,
                right: null
            }
        },
        right: {
            val: 3,
            left: {
                val: 6,
                left: null,
                right: null
            },
            right: {
                val: 7,
                left: null,
                right: null
            },
        }
    }
    const preorder=(root)=>{
        if(!root) return
        console.log(root.val)
        preorder(root.left)
        preorder(root.right)
    }
    preorder(bt)
    const inorder=(root)=>{
        if(!root) return
        inorder(root.left)
        console.log(root.val)
        inorder(root.right)
    }
    inorder(bt)
    const postorder=(root)=>{
        if(!root) return
        postorder(root.left)
        postorder(root.right)
        console.log(root.val)
    }
    postorder(bt)

7.4二叉树的先/中/后序遍历（非递归版）

栈就是我们去实现非递归版的一个核心，所有的递归都可以用栈来解决。

    const bt = {
        val: 1,
        left: {
            val: 2,
            left: {
                val: 4,
                left: null,
                right: null
            },
            right: {
                val: 5,
                left: null,
                right: null
            }
        },
        right: {
            val: 3,
            left: {
                val: 6,
                left: null,
                right: null
            },
            right: {
                val: 7,
                left: null,
                right: null
            },
        }
    }
    // 前序遍历非递归版
    const preorder=(root)=>{
        if(!root) return
        const stack=[root]
        while(stack.length){
            const n=stack.pop()
            console.log(n.val)
            if(n.right) stack.push(n.right)
            if(n.left) stack.push(n.left)
        }
    }
    preorder(bt)
    // 中序遍历非递归版
    const inorder=(root)=>{
        if(!root) return
        const stack=[]
        let p=root
        while(stack.length||p){
            while(p){
                stack.push(p)
                p=p.left
            }
            const n=stack.pop()
            console.log(n.val)
            p=n.right
        }
    }
    inorder(bt)
    // 后序遍历非递归版
    const postorder=(root)=>{
        if(!root) return
        const stack=[root]
        const outputStack=[]
        while(stack.length){
            const n=stack.pop()
            outputStack.push(n)
            if(n.left) stack.push(n.left)
            if(n.right) stack.push(n.right)
        }
        while(outputStack.length){
            const n=outputStack.pop()
            console.log(n.val)
        }
    }
    postorder(bt)

下面是leetcode里的104题?

var maxDepth = function (root) {
    let res = 0
    const dfs = (root, n) => {
        if (!root) return
        console.log(root.val, n)
        res = Math.max(res, n)
        dfs(root.left,n+1)
        dfs(root.right,n+1)
    }
    dfs(root, 1)
    return res
};

?下面是leetcode里的111题?

var minDepth = function(root) {
    if(!root) return 0
    const stack=[[root,1]]
    while(stack.length>0){
        const [n,l]=stack.shift()
        if(!n.left&&!n.right) return l
        if(n.left) stack.push([n.left,l+1])
        if(n.right) stack.push([n.right,l+1])
    }
};

下面是leetcode里的102题?

//解法一
var levelOrder = function (root) {
    if (!root) { return [] }
    let res = []
    let stack = [[root, 0]]
    while (stack.length) {
        let [n, l] = stack.shift()
        if (!res[l]) {
            if(n) res.push([n.val])
        } else {
            if(n) res[l].push(n.val)
        }
        if (n.left) stack.push([n.left, l + 1])
        if (n.right) stack.push([n.right, l + 1])
    }
    return res
};
//解法二
var levelOrder = function (root) {
    if (!root) { return [] }
    let res = []
    let stack = [root]
    while (stack.length) {
        let len = stack.length
        res.push([])
        while (len--) {
            const n = stack.shift()
            res[res.length-1].push(n.val)
            if (n.left) stack.push(n.left)
            if (n.right) stack.push(n.right)
        }
    }
    return res
};

下面是leetcode里的94题?

var inorderTraversal = function(root) {
    const res=[]
    const stack=[]
    const rec=(n)=>{
        if(!n) return 
        rec(n.left)
        res.push(n.val)
        rec(n.right)
    }
    rec(root)
    return res
};

?下面是leetcode里的112题?

var hasPathSum = function(root, targetSum) {
   if(!root) return false
   let flag=false
    const dfs=(root,s)=>{
        if(!root.left&&!root.right){
            if(s===targetSum) {
                flag=true
                return
            }
        }
        if(root.left) dfs(root.left,root.left.val+s)
        if(root.right) dfs(root.right,root.right.val+s)
    }
    dfs(root,root.val)
    return flag
};

7.5使用深度遍历算法遍历json的所有节点值（前面在链表中我们也遍历过json，但是比较low）

const json = {
    a: { b: { c: 1 } },
    d: [1,2],
}
const dfs1=(n,path)=>{
    console.log(n,path)
    Object.keys(n).forEach(k=>{
        dfs1(n[k],path.concat(k))
    })
}
dfs1(json,[])

对json数据深度优先遍历或者说是树的深度优先遍历用的很多，我们前端有时候将json的数据深度遍历成antd的组件，就需要深度优先遍历，所以我们要对深度优先遍历了然于心。

8.图

图是网络结构的抽象模型，是一组由边连接的节点。

8.1js中如何用图

在js中我们没有图，但是可以用Object和Array构建图

前端工作中常见的树包括：图可以表示任何的二元关系，道路，航班...

图的表示法：邻接矩阵，邻接表，关联矩阵

8.2图的邻接矩阵表示法

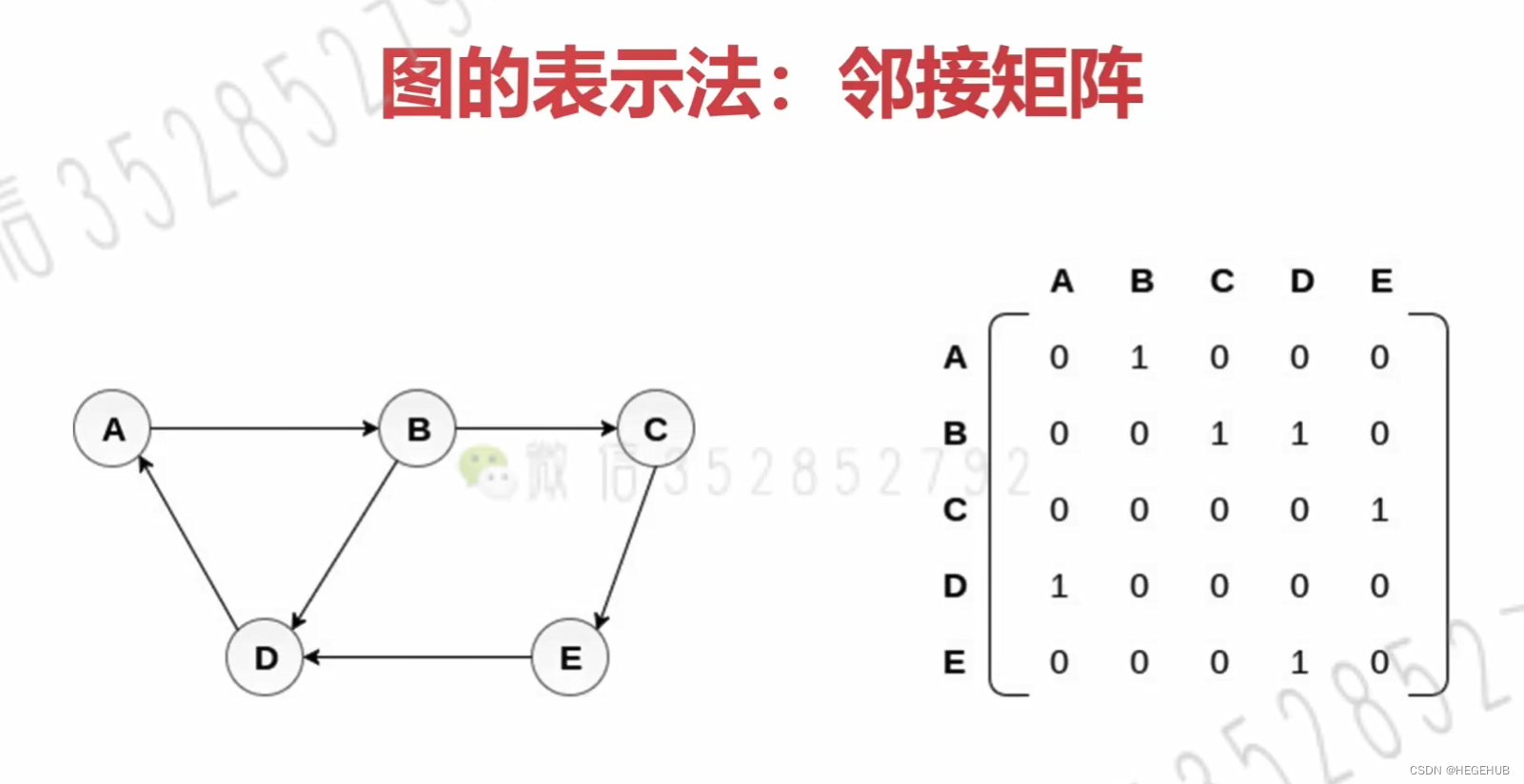
?8.3图的邻接表表示法

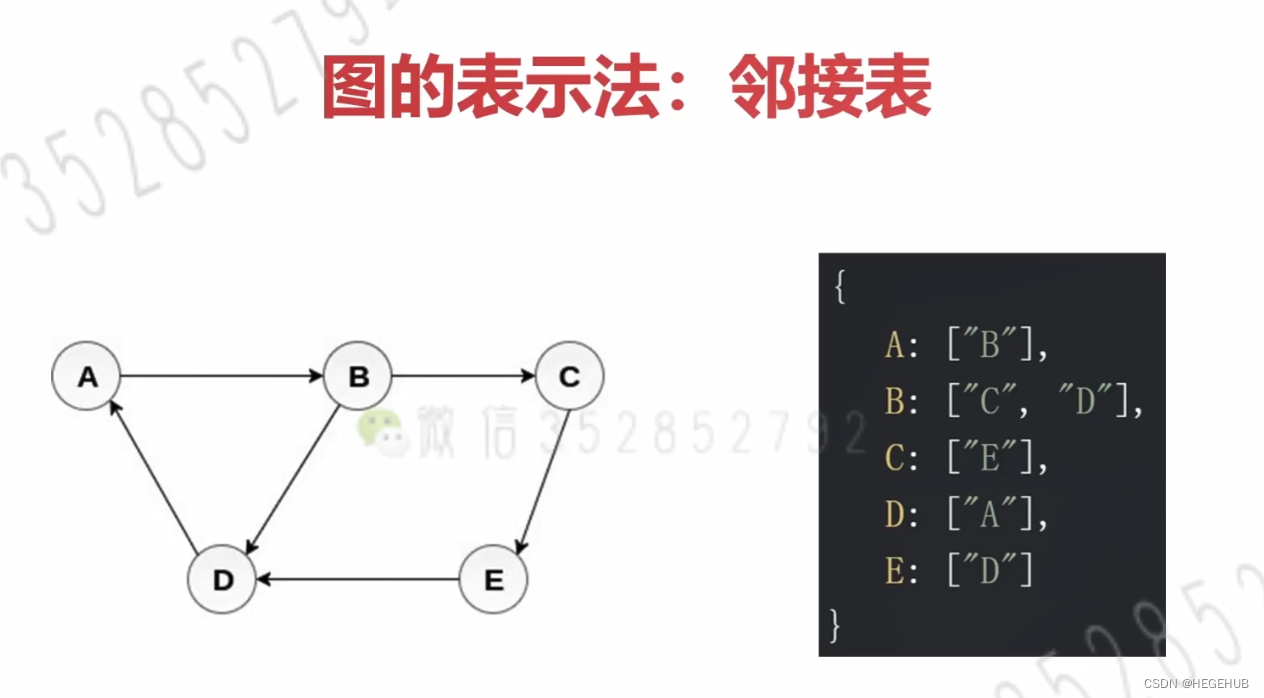
?图的邻接表表示法可以用数组，也可以用链表来表示，只要能表现出两者之间的关系就好。

8.4图的常用操作

深度优先遍历

广度优先遍历

8.5什么是图的深度/广度优先遍历

深度优先遍历算法口诀

访问根节点
对根节点的没访问过的相邻节点挨个进行深度优先遍历

广度优先遍历算法口诀

新建一个队列，把根节点入队
把队头出队并访问
把队头的没访问过的相邻节点入队
重复第二三步，直到队列为空

    //图的深度遍历
    const graph = {
        0: [1, 2],
        1: [2],
        2: [0, 3],
        3: [3]
    }
    const visited = new Set()
    const dfs2 = (n) => {
        console.log(n)
        visited.add(n)
        graph[n].forEach(c => {
            if (!visited.has(c)) {
                dfs2(c)
            }
        })
    }
    dfs2(2)//起始节点为2

    //图的广度遍历
    const visited1 = new Set()
    const q = [2]
    visited.add(2)
    while (q.length) {
        const n = q.shift()
        console.log(n)
        // visited.add(n)//这句话写在这有问题，有的节点在队列里面但是并没有被访问过，这样就会导致一直重复向队列添加重复元素
        // 所以我们入队的时候就将认为其访问过了，可以防止队列出现重复元素，这样会导致起始节点不在visited中，我们加一下就好了
        graph[n].forEach(c => {
            if (!visited.has(c)) {
                q.push(c)
                visited.add(n)
            }
        })
    }

?下面是leetcode里的65题?

var isNumber = function (s) {
    const graph = {
        0: { 'blank': 0, 'sign': 1, '.': 2, 'digit': 6 },
        1: { 'digit': 6, '.': 2 },
        2: { 'digit': 3 },
        3: { 'digit': 3, 'e': 4 },
        4: { 'digit': 5, 'sign': 7 },
        5: { 'digit': 5 },
        6: { 'digit': 6, '.': 3, 'e': 4 },
        7: { 'digit': 5 },
    }
    let state = 0//刚开始的状态
    for (c of s.trim()) {//trim用于去掉前后的空格，降低复杂度
        if (c >= '0' && c <= '9') {
            c = 'digit'
        } else if (c === ' ') {
            c = 'blank'
        } else if (c === '+' || c === '-') {
            c = 'sign'
        } else if (c === 'e' || c === 'E') {
            c = 'e'
        }
        state = graph[state][c]//获取下一个状态
        if (state === undefined) {
            return false
        }
    }
    if (state === 3 || state === 5 || state === 6) {
        return true
    }
    return false
};

??下面是leetcode里的133题?

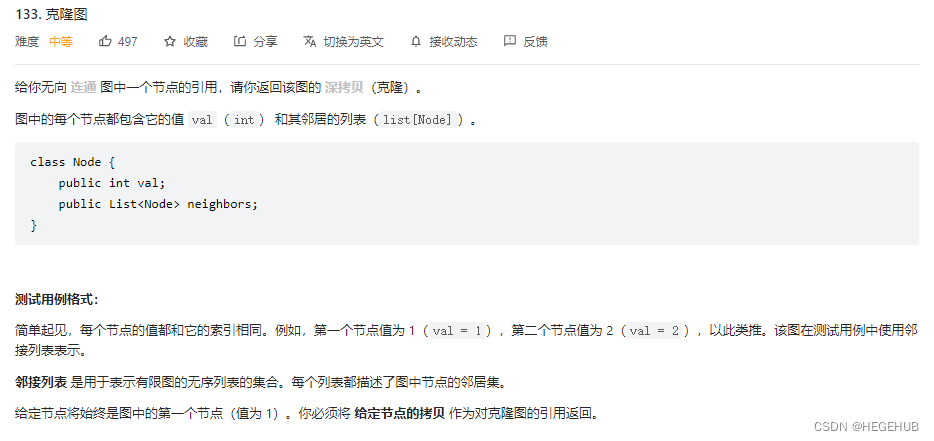
var cloneGraph = function(node) {
    if(!node) return
    const visited=new Map()
    const dfs=(n)=>{
        const nCopy=new Node(n.val)
        visited.set(n,nCopy)
        //防止neighbors为undefined
        n.neighbors.forEach(ne=>{
            if(!visited.has(ne)){
                dfs(ne)
            }
            nCopy.neighbors.push(visited.get(ne))
        })
    }
    dfs(node)
    return visited.get(node)
};

上面这道题也可以用广度优先遍历去做

图中还有一个大西洋太平洋水流问题没有解决，待更新。

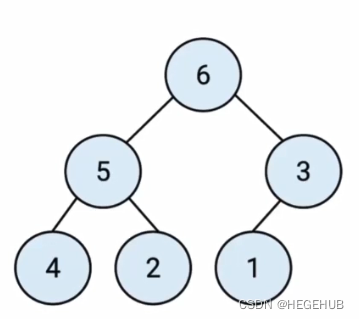
9.堆

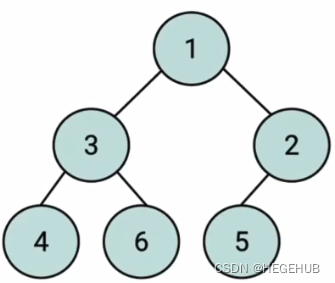
堆是一种特殊的完全二叉树（要注意完全二叉树和满二叉树的区别）

所有的节点都大于等于（最大堆）或小于等于（最小堆）他/它的子节点。

最大堆：

?最小堆：

9.1js中如何用堆

在js中我们没有堆，但是可以用Array表示堆。

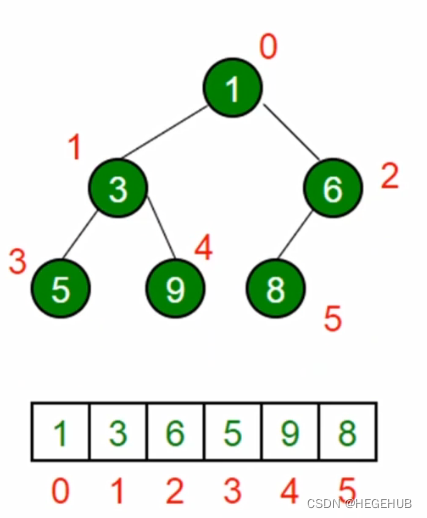
还可以通过公式来获取子节点或者父节点的位置。

左侧子节点位置：2*index+1

右侧子节点位置：2*index+2

父节点位置：（index-1）/2?

堆的应用：

堆能高效，快速的找出最大值（最大堆的第一个元素）和最小值（最小堆的第一个元素），事件复杂度为O（1）
找出第K个最大（小）元素（看到这种问题直接用堆解决）

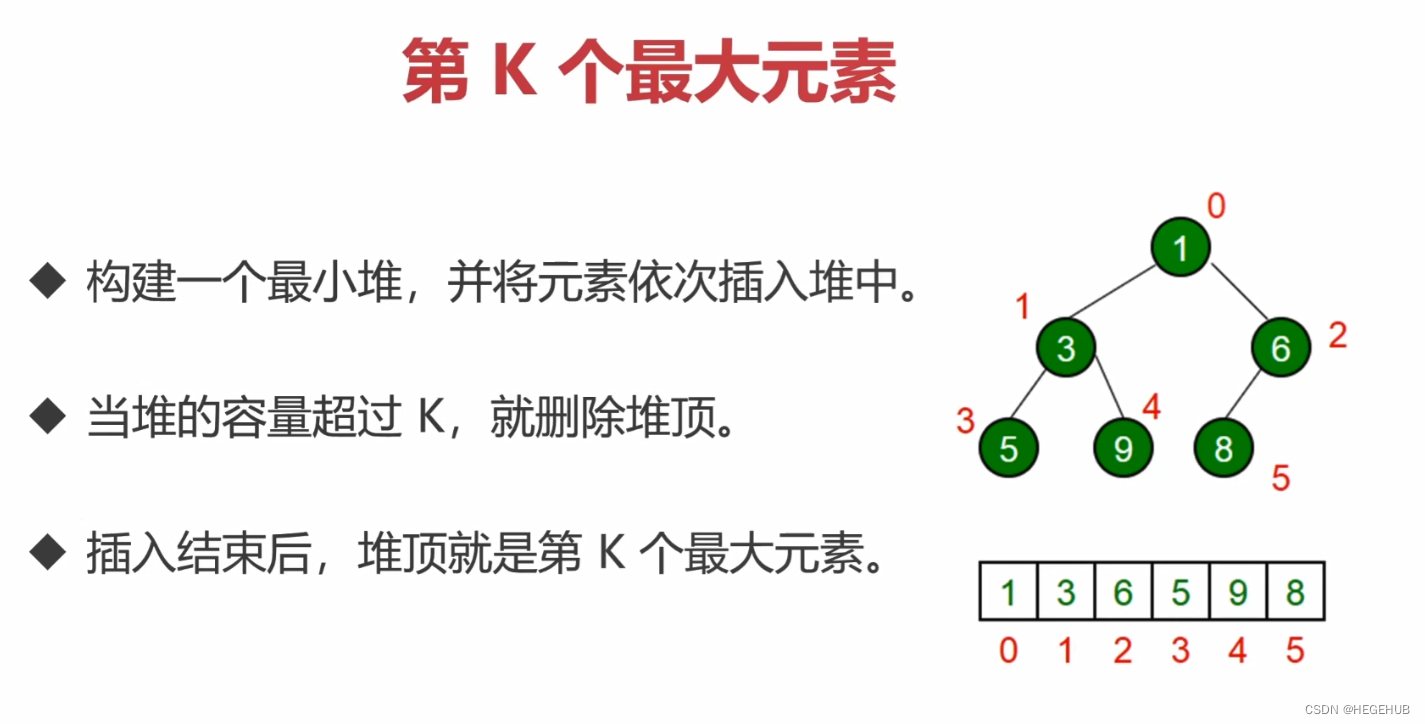
第K个最大元素（找第K个最小元素和这个逻辑是一样的）

9.3用js实现一个最小堆类

最小堆：

在类里声明一个数组，用来装元素
主要方法：插入，删除堆顶，获取堆顶，获取堆大小。

插入：

将值插入堆的底部，即数组尾部
然后上移：将这个值和它的父节点进行交换，直到父节点小于等于这个插入的值
大小为K的堆中插入元素的时间复杂度为O（logk）

删除：

用数组尾部元素替换堆顶（直接删除堆顶会破坏堆结构）
然后下移：将新堆顶和它的子节点进行交换，知道子节点大于等于这个新堆顶。
大小为k的堆中删除堆顶的时间复杂度为O（logk）

返回堆顶：

返回对应数组下标为0的元素

返回堆大小

返回对应数组的长度

    class MinHeap{
        constructor(){
            this.heap=[]
        }
        getLeftIndex(index){
            return index*2+1
        }
        getRightIndex(index){
            return index*2+2
        }
        getParentIndex(i){
            // return Math.floor((i-1)/2)
            return i-1>>1//二进制数右移一位，就相当于是除2
        }
        swap(i1,i2){
            const temp=this.heap[i1]
            this.heap[i1]=this.heap[i2]
            this.heap[i2]=temp
        }
        shiftUp(index){
            if(index===0) return 
            // 获取父节点的Index的方法
            const parentIndex=this.getParentIndex(index)
            if(this.heap[parentIndex]>this.heap[index]){
                this.swap(parentIndex,index)
                this.shiftUp(parentIndex)
            }
        }
        shiftDown(index){
            // if(index===this.heap.lenght-1) return 
            const leftIndex=this.getLeftIndex(index)
            const rightIndex=this.getRightIndex(index)
            if(this.heap[leftIndex]<this.heap[index]){
                this.swap(leftIndex,index)
                this.shiftDown(leftIndex)
            }
            if(this.heap[rightIndex]<this.heap[index]){
                this.swap(rightIndex,index)
                this.shiftDown(rightIndex)
            }
        }
        inset(value){
            this.heap.push(value)
            //上移操作方法,数组最后一位的下标
            this.shiftUp(this.heap.length-1)
        }
        pop(){
            this.heap[0]=this.heap.pop()
            this.shiftDown(0)
        }
        peek(){
            return this.heap[0]
        }
        size(){
            return this.heap.length
        }
    }
    const h=new MinHeap()
    h.inset(3)//将3出堆
    h.inset(2)//将2出堆
    h.inset(1)//将1出堆
    console.log(h.peek())//1
    console.log(h.size())//3
    h.pop()//将1出堆
    console.log(h.peek())//2
    console.log(h.size())//2

?下面是leetcode里的215题?

class MinHeap {
    constructor() {
        this.heap = []
    }
    getLeftIndex(index) {
        return index * 2 + 1
    }
    getRightIndex(index) {
        return index * 2 + 2
    }
    getParentIndex(i) {
        // return Math.floor((i-1)/2)
        return i - 1 >> 1//二进制数右移一位，就相当于是除2
    }
    swap(i1, i2) {
        const temp = this.heap[i1]
        this.heap[i1] = this.heap[i2]
        this.heap[i2] = temp
    }
    shiftUp(index) {
        if (index === 0) return
        // 获取父节点的Index的方法
        const parentIndex = this.getParentIndex(index)
        if (this.heap[parentIndex] > this.heap[index]) {
            this.swap(parentIndex, index)
            this.shiftUp(parentIndex)
        }
    }
    shiftDown(index) {
        // if(index===this.heap.lenght-1) return 
        const leftIndex = this.getLeftIndex(index)
        const rightIndex = this.getRightIndex(index)
        if (this.heap[leftIndex] < this.heap[index]) {
            this.swap(leftIndex, index)
            this.shiftDown(leftIndex)
        }
        if (this.heap[rightIndex] < this.heap[index]) {
            this.swap(rightIndex, index)
            this.shiftDown(rightIndex)
        }
    }
    insert(value) {
        this.heap.push(value)
        //上移操作方法,数组最后一位的下标
        this.shiftUp(this.heap.length - 1)
    }
    pop() {
        this.heap[0] = this.heap.pop()
        this.shiftDown(0)
    }
    peek() {
        return this.heap[0]
    }
    size() {
        return this.heap.length
    }
}
/**
 * @param {number[]} nums
 * @param {number} k
 * @return {number}
 */
var findKthLargest = function (nums, k) {
    const h = new MinHeap()
    nums.forEach(n => {
        h.insert(n)
        if (h.size() > k) {
            h.pop()
        }
    })
    return h.peek()
};

?下面是leetcode里的347题?

    class MinHeap{
        constructor(){
            this.heap=[]
        }
        getLeftIndex(index){
            return index*2+1
        }
        getRightIndex(index){
            return index*2+2
        }
        getParentIndex(i){
            // return Math.floor((i-1)/2)
            return i-1>>1//二进制数右移一位，就相当于是除2
        }
        swap(i1,i2){
            const temp=this.heap[i1]
            this.heap[i1]=this.heap[i2]
            this.heap[i2]=temp
        }
        shiftUp(index){
            if(index===0) return 
            // 获取父节点的Index的方法
            const parentIndex=this.getParentIndex(index)
            if(this.heap[parentIndex]&&this.heap[parentIndex].value>this.heap[index].value){
                this.swap(parentIndex,index)
                this.shiftUp(parentIndex)
            }
        }
        shiftDown(index){
            // if(index===this.heap.lenght-1) return 
            const leftIndex=this.getLeftIndex(index)
            const rightIndex=this.getRightIndex(index)
            if(this.heap[leftIndex]&&this.heap[leftIndex].value<this.heap[index].value){
                this.swap(leftIndex,index)
                this.shiftDown(leftIndex)
            }
            if(this.heap[rightIndex]&&this.heap[rightIndex].value<this.heap[index].value){
                this.swap(rightIndex,index)
                this.shiftDown(rightIndex)
            }
        }
        insert(value){
            this.heap.push(value)
            //上移操作方法,数组最后一位的下标
            this.shiftUp(this.heap.length-1)
        }
        pop(){
            this.heap[0]=this.heap.pop()
            this.shiftDown(0)
        }
        peek(){
            return this.heap[0]
        }
        size(){
            return this.heap.length
        }
    }
/**
 * @param {number[]} nums
 * @param {number} k
 * @return {number[]}
 */
var topKFrequent = function(nums, k) {
    const map=new Map()
    nums.forEach(c=>{
        if(!map.has(c)){
            map.set(c,1)
        }else{
            map.set(c,map.get(c)+1)
        }
    })
    const h=new MinHeap()
    map.forEach((value,key)=>{
        h.insert({value,key})
        if(h.size()>k){
            h.pop()
        }
    })
    return h.heap.map(a=>a.key)
};

?下面是leetcode里的23题?

对数组排序的时间复杂度最小为O（nlogn），但是我们没必要对整个数组进行排序，我们只需要找到最小值就好了，所以这个时候我们没有必要用数组，我们就可以用最小堆来（时间复杂度logk）实现。

class MinHeap{
        constructor(){
            this.heap=[]
        }
        getLeftIndex(index){
            return index*2+1
        }
        getRightIndex(index){
            return index*2+2
        }
        getParentIndex(i){
            // return Math.floor((i-1)/2)
            return i-1>>1//二进制数右移一位，就相当于是除2
        }
        swap(i1,i2){
            const temp=this.heap[i1]
            this.heap[i1]=this.heap[i2]
            this.heap[i2]=temp
        }
        shiftUp(index){
            if(index===0) return 
            // 获取父节点的Index的方法
            const parentIndex=this.getParentIndex(index)
            if(this.heap[parentIndex]&&this.heap[parentIndex].val>this.heap[index].val){
                this.swap(parentIndex,index)
                this.shiftUp(parentIndex)
            }
        }
        shiftDown(index){
            // if(index===this.heap.lenght-1) return 
            const leftIndex=this.getLeftIndex(index)
            const rightIndex=this.getRightIndex(index)
            if(this.heap[leftIndex]&&this.heap[leftIndex].val<this.heap[index].val){
                this.swap(leftIndex,index)
                this.shiftDown(leftIndex)
            }
            if(this.heap[rightIndex]&&this.heap[rightIndex].val<this.heap[index].val){
                this.swap(rightIndex,index)
                this.shiftDown(rightIndex)
            }
        }
        insert(value){
            this.heap.push(value)
            //上移操作方法,数组最后一位的下标
            this.shiftUp(this.heap.length-1)
        }
        pop(){
            if(this.size()===1) return this.heap.shift()
            const top=this.heap[0]
            this.heap[0]=this.heap.pop()
            this.shiftDown(0)
            return top
        }
        peek(){
            return this.heap[0]
        }
        size(){
            return this.heap.length
        }
    }
/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode[]} lists
 * @return {ListNode}
 */
var mergeKLists = function(lists) {
    const res=new ListNode(0)
    let p=res
    const h=new MinHeap()
    lists.forEach(l=>{
        if(l) h.insert(l)
    })
    while(h.size()){
        const n=h.pop()
        p.next=n
        p=p.next
        if(n.next) h.insert(n.next)
    }
    return res.next
};

10.排序和搜索

排序：把某个乱序的数组变成升序或者降序的数组

搜索：找出数组中某个元素的下标

10.1js中的排序和搜索

js中的排序：数组的sort方法等。
js中的搜索：数组的indexOf方法等。

为什么有了现成的API我们还要学习排序和搜索呢，因为我们程序员不仅要知其然还要知其所以然，了解其原理，丛0开始学习排序和搜索。

10.2常用的搜索和排序算法

排序算法：冒泡排序，归并排序，选择排序，插入排序，快速排序等等
搜索算法：顺序搜索，二分搜索等等

10.3js实现冒泡排序

比较所有相邻元素，如果第一个比第二个大，则交换它们。
一轮下来，可以保证最后一个数是最大的。
执行n-1轮，就可以完成排序。（最后一个数不用排了）

    Array.prototype.bubbleSort=function(){
        for(let i=0;i<this.length-1;i++){
            for(let j=0;j<this.length-1-i;j++){
                if(this[j]>this[j+1]){
                    let temp=this[j]
                    this[j]=this[j+1]
                    this[j+1]=temp
                }
            }
        }
    }

10.4js实现选择排序

找到数组中的最小值，选中它并将其放置在第一位
接着找到第二小的值，选中它并将其放置在第二位
以此类推执行n-1轮

    Array.prototype.selectionSort = function () {
        for (let i = 0; i < this.length - 1; i++) {
            let min=i//默认刚开始的值时最小的
            for (let j = i; j < this.length  ; j++) {
                if (this[min] > this[j]) {
                    min = j 
                }
            }
            if (i !== min) {
                let temp = this[i]
                this[i]=this[min]
                this[min]=temp
            }
        }
    }

10.5js实现插入排序

从第二个数开始往前比
比它大就往后排
以此类推进行到最后一个数

    Array.prototype.insertionSort = function () {
        for (let i = 1; i < this.length; i++) {
            let currentValue=this[i]
            let j=i
            for (j; j >0;j--) {
                if (currentValue < this[j-1]) {
                    this[j]=this[j-1]
                }else {
                    break
                }
            }
            this[j]=currentValue
        }
    }

10.6js实现归并排序

火狐浏览器里面的sort算法就是用的归并排序来实现的

分：把数组劈成两半，再递归地对子数组进行分操作，直到分成一个一个单独的数的数组
合：把两个数合并为有序数组，再对有序数组进行合并，直到全部子数组合并为一个完整数组

如何合并两个有序数组

新建一个空数组res，用于存放最终排序后的数组
比较两个有序数组的头部，较小者出队并推入res中
如果两个数组还有值，就重复第二步

    Array.prototype.mergeSort = function () {
        const rec=(arr)=>{
            if (arr.length===1) return arr
            const mid=Math.floor(arr.length/2)
            const left=arr.slice(0,mid)
            const right=arr.slice(mid,arr.length)
            const orderLeft=rec(left)
            const orderRight=rec(right)
            const res=[]
            while(orderLeft.length||orderRight.length){
                if(orderLeft.length&&orderRight.length){
                    res.push(orderLeft[0]<orderRight?orderLeft.shift():orderRight.shift())
                }else if(orderRight.length){
                    res.push(orderRight.shift())
                }else if(orderLeft.length){
                    res.push(orderLeft.shift())
                }
            }
            return res
        }
        const  res=rec(this)
        console.log(res)
        res.forEach((n,i)=>{this[i]=n})
    }

10.7js实现快速排序

Chrome浏览器里面的sort就是用的快速排序来实现的

分区：从数组中任意选择一个基准，所有比基准小的元素放在基准前面，比基准大的放在基准后面
递归：递归地对基准前后的子数组进行分区

    Array.prototype.quickSort = function () {
        const rec=(arr)=>{
            if(arr.length<=1) return arr
            const left=[]
            const right=[]
            const mid=arr[0]
            for(let i=1;i<arr.length;i++){
                if(arr[i]<mid){
                    left.push(arr[i])
                }else{
                    right.push(arr[i])
                }
            }
            return [...rec(left),mid,...rec(right)]
        }
        const  res=rec(this)
        res.forEach((n,i)=>{this[i]=n})
    }

10.8js实现顺序搜索

遍历数组
找到跟目标值相等的元素，就返回它的下标
遍历结束后，如果没有搜索到目标值，就返回-1

    Array.prototype.sequentialSearch = function (num) {
        for(let i=0;i<this.length;i++){
            if(this[i]===num){
                return i
            }
        }
        return -1
    }

10.9js实现二分搜索（折半搜索）

针对于有序数组

从数组的中间元素开始，如果中间元素正好是目标值，则搜索结束
如果目标值大于或者小于中间元素，则在大于或者小于中间元素的那一半数组中搜索

    Array.prototype.binarySearch = function (num) {
        let low=0
        let high=this.length-1
        while(low<=high){
            const mid =Math.floor((low+high)/2)
            const element=this[mid]
            if(element<num){
                low=mid+1
            }else if(element>num){
                high=mid-1
            }else{
                return mid
            }
        }
        return -1
    }

下面是leetcode里的21题?

var mergeTwoLists = function (list1, list2) {
    const res = new ListNode(0)
    let h3 = res
    let h1 = list1
    let h2 = list2
    while (h1 && h2) {
        if (h1.val <= h2.val) {
            h3.next = h1
            h1 = h1.next
        } else {
            h3.next = h2
            h2 = h2.next
        }
        h3 = h3.next
    }
    if (h1) {
        h3.next = h1
    }
    if (h2) {
        h3.next = h2
    }
    return res.next
};

下面是leetcode里的374题?

var guessNumber = function(n) {
    let low=1
    let high=n
    while(low<=high){
        const mid=Math.floor((low+high)/2)
         const res=guess(mid)
        if(res===0){
            return mid
        }else if(res===1){
            low=mid+1
        }else{
            high=mid-1
        }
    }
};

非常感谢您的阅读，欢迎大家提出您的意见，指出相关错误，谢谢！越努力，越幸运！