零、导言
这一系列博客的创作初衷是为了记录自己在刷题过程中对于一些比较经典的并且很哇塞的题型的所思所想,巩固所学,即时复盘。 正因为是为了便于自己复盘,所以大多是以自己的思维模式书写。如果小伙伴们在阅读的时候发现什么错误、对内容有疑问以及对书写排版等有改进意见的话,请评论区留言指正!一、例子引入
1、题目描述
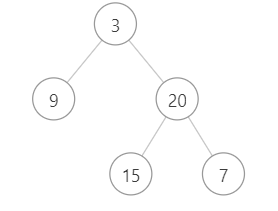
??从上到下打印出二叉树的每个节点,同一层的节点按照从左到右的顺序打印。
输入:
返回:
[3,9,20,15,7] \texttt{[3,9,20,15,7]} [3,9,20,15,7]
2、题目分析
??(1)题目中明确说明了是按照层进行遍历输出的,也就是层序遍历。有别于树的遍历中的 前序、中序以及后续遍历中使用的深度优先搜索,这里是利用 广度优先搜索 实现的层序遍历;
??(2)具体的做法就是维护一个队列 q 和一个答案容器 ret :队列用来存放树的节点,答案容器用来存放最终的输出答案。
- 首先把根节点存入队列
q; - 队列只要不为空就一直循环读取队列中的队首元素:
??当前读取的队首元素存入ret,当当前读取的队首元素还有子节点的话依次把左子节点、右子节点存入队列;
??(3)可能会有人说,这是二叉树所以知道是有左子树和右子树,那要是 N叉树 的情况,怎么知道到底有几点子节点呢?这个就要看树的结构了,一般在答题区域都会有已经实现了的结构体或类了。可以参照 LeetCode 429. N 叉树的层序遍历 中答题区域的 N叉树 数据结构的实现。
3、算法实现与解释
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector<int> levelOrder(TreeNode* root) {
if(root == NULL){
return {};
}
vector<int> ret;
queue<TreeNode*> Q;
Q.push(root); // push根节点
while(!Q.empty()){ // 循环的条件
TreeNode* now = Q.front(); // 读取队首元素
ret.push_back(now->val); // push进答案容器
Q.pop();
if(now->left){ // 判断是否有左子节点
Q.push(now->left);
}
if(now->right){ // 判断是否有右子节点
Q.push(now->right);
}
}
return ret;
}
};
二、概念定义
例子看完了,相信大家对这个题目以及 广度优先搜索——层序遍历 已经有了初步的认识了。现在我们来详细解读一下广度优先搜索和层序遍历。
1、定义
维基百科 广度优先搜索算法 (英语:Breadth-First Search,缩写为BFS),又译作 宽度优先搜索 ,或 横向优先搜索 ,是一种图形搜索算法。简单的说,BFS是从根节点开始,沿着树的宽度遍历树的节点。如果所有节点均被访问,则算法中止。广度优先搜索的实现一般采用open-closed表。
层序遍历: 是树众多遍历算法中的一种。有前序遍历、中序遍历、后续遍历和层序遍历等等。
以上提及的遍历方法的定义以及求解方法见下表所示:
| 项目 | 含义(以二叉树为例) | 方法 |
|---|---|---|
| 层序遍历 | 按层对树进行遍历,每一层从左往右依次遍历 | BFS |
| 前序遍历 | 按照先左子节点再根节点,最后再遍历右子节点的顺序对一棵树进行遍历 | DFS |
| 中序遍历 | 按照先根节点再左子节点,最后再遍历右子节点的顺序对一棵树进行遍历 | DFS |
| 后续遍历 | 按照先右子节点再根节点,最后再遍历左子节点的顺序对一棵树进行遍历 | DFS |
2、深入理解
通过做一些广搜类和深搜类的算法题目,我们可以发现:
- 对于深搜类的题目会用到 栈 这种数据结构(一般会使用
vector<>容器来代替); - 对于广搜类的题目,我们会使用到
queue<>队列 这种数据结构,有时候也会使用priority_queue<>优先队列 这种数据结构
那为什么会是这样呢?
还是要从定义出发,以树结构为例:
- 深搜要一头扎到底,从树的根节点一直扎到叶子节点,然后再慢慢的回溯,这就会涉及到 后入先出 的问题,具体的在 深度优先搜索 的章节再细讲。
- 广度优先搜索,广搜从树的根节点开始,沿着树的宽度方向开始搜索,依次加入当前层的各个子节点,然后再依次读取各个子节点的子节点。直到队列为空,结束循环。
以例子中的二叉树为例:

3、相关知识
通过以上的分析,可以发现熟知 队列 的相关操作是十分必要的。
参照 四、总结(4)回顾队列知识。
三、相关习题
| 题号 | 难度 |
|---|---|
| 剑指 Offer 32 - I. 从上到下打印二叉树 | 中等 |
| 剑指 Offer 32 - II. 从上到下打印二叉树 II | 简单 |
| 剑指 Offer 32 - III. 从上到下打印二叉树 III | 中等 |
| 429. N 叉树的层序遍历 | 中等 |