一、最短路问题
设给定一个带权有向图 G = ( V , E ) G=(V,E) G=(V,E),源点为 s s s,求 s s s到 G G G中其他各点之间的最短路径,这类问题称为单源最短路径问题。
记顶点 s s s到点 u u u的最短路径为 δ ( u ) \delta(u) δ(u),正在计算的点 s s s到点 u u u可能的最短路径为 d ( u ) d(u) d(u)。记边 ( u , v ) (u,v) (u,v)的权重为 w ( u , v ) w(u,v) w(u,v),路径 Γ \Gamma Γ的长度为 w ( Γ ) w(\Gamma) w(Γ)。
定理(最短路问题的最优子结构性质) 设路径
Γ
\Gamma
Γ是点
u
u
u到
v
v
v的最短路径,
p
,
q
p,q
p,q在
Γ
\Gamma
Γ上,即
Γ
:
u
→
p
?
Γ
p
→
q
q
→
v
\Gamma:u\to p\overset{\Gamma_{p\to q}}{\longrightarrow}q\to v
Γ:u→p?Γp→q??q→v,则
Γ
\Gamma
Γ在
p
p
p和
q
q
q之间的部分
Γ
p
→
q
\Gamma_{p\to q}
Γp→q?是
p
p
p到
q
q
q的一条最短路径。
证明:采用反证法。假设
Γ
p
→
q
\Gamma_{p\to q}
Γp→q?不是
p
p
p到
q
q
q的最短路径,则取
p
p
p到
q
q
q的最短路径
Σ
p
→
q
\Sigma_{p\to q}
Σp→q?,于是
u
u
u到
v
v
v有一条比
Γ
\Gamma
Γ更短的路径
u
→
p
?
Σ
p
→
q
q
→
v
u\to p\overset{\Sigma{p\to q}}{\longrightarrow}q\to v
u→p?Σp→q?q→v,与
Γ
\Gamma
Γ是点
u
u
u到
v
v
v的最短路径矛盾。因此假设不成立,定理证毕。?
二、Dijkstra算法
基本思想
Dijkstra算法要求 ? e ∈ E , w ( e ) ≥ 0 \forall e\in E,w(e)\ge 0 ?e∈E,w(e)≥0。即:图中的边权必为非负值。
(1) 将图 G G G的顶点集 V V V划分为两个集合 S S S和 V ? S V-S V?S,集合 S S S存放已经确定了最短路径的顶点集合。令 d ( u ) = { 0 , u = s + ∞ , u ≠ s d(u)=\begin{cases}0,&u=s\\+\infty,&u\ne s\end{cases} d(u)={0,+∞,?u=su?=s?初始状态时, S = ? S=\emptyset S=?。
(2)不断重复以下过程,直到 S = V S=V S=V为止:
- 选择顶点 u u u,使得 d ( u ) = min ? v ∈ V ? S d ( v ) d(u)=\min\limits_{v\in V-S}d(v) d(u)=v∈V?Smin?d(v)。
- 我们断言 u u u一定满足 d ( u ) = δ ( u ) d(u)=\delta(u) d(u)=δ(u),即 d ( u ) d(u) d(u)是 s s s到 u u u的最短路径。将 u u u并入 S S S中,即 S = S ∪ { u } S=S\cup\{u\} S=S∪{u}。
- 修改与 u u u相连的节点的 d d d值(称为“松弛”操作)。 ? v ∈ V ? S \forall v\in V-S ?v∈V?S且 ( u , v ) ∈ E (u,v)\in E (u,v)∈E,令 d ( v ) = min ? { d ( v ) , d ( u ) + w ( u , v ) } d(v)=\min\{d(v),d(u)+w(u,v)\} d(v)=min{d(v),d(u)+w(u,v)}。若 d ( v ) d(v) d(v)确实变小了,则设 v v v在 s s s到 v v v的最短路径中的前驱节点 prev ( v ) = u \text{prev}(v)=u prev(v)=u。最终, s s s到 v v v的最短路径是 s , ? ? , prev ( prev ( prev ( v ) ) ) , prev ( prev ( v ) ) , prev ( v ) , v s,\cdots,\text{prev}(\text{prev}(\text{prev}(v))),\text{prev}(\text{prev}(v)),\text{prev}(v),v s,?,prev(prev(prev(v))),prev(prev(v)),prev(v),v。
正确性证明
引理1 设算法第(2)步求出 u u u满足 d ( u ) = min ? v ∈ V ? S d ( v ) d(u)=\min\limits_{v\in V-S}d(v) d(u)=v∈V?Smin?d(v), s s s到 u u u的路径 Γ ( u ) = ( s , ? ? , prev ( prev ( u ) ) , prev ( u ) , u ) \Gamma(u)=(s,\cdots,\text{prev}(\text{prev}(u)),\text{prev}(u),u) Γ(u)=(s,?,prev(prev(u)),prev(u),u),则 Γ ( u ) \Gamma(u) Γ(u)中除了 u u u以外所有的节点都属于 S S S,即 s , ? ? , prev ( prev ( u ) ) , prev ( u ) ∈ S s,\cdots,\text{prev}(\text{prev}(u)),\text{prev}(u)\in S s,?,prev(prev(u)),prev(u)∈S。
证明:
归纳基础:当 S = ? S=\emptyset S=?时, u = s u=s u=s, Γ ( s ) = ( s ) \Gamma(s)=(s) Γ(s)=(s),其中除了 s s s之外没有节点,所以都属于 S S S。
归纳步:假设对 S = S k S=S_k S=Sk?时成立。设 u u u满足 d ( u ) = min ? v ∈ V ? S k d ( v ) d(u)=\min\limits_{v\in V-S_k}d(v) d(u)=v∈V?Sk?min?d(v),观察Dijkstra算法的步骤,当节点 v v v的 prev \text{prev} prev值被修改为 u k u_k uk?,即 u k u_k uk?对节点 v v v执行松弛操作时, u k u_k uk?必已并入 S S S中,即 prev ( v ) ∈ S \text{prev}(v)\in S prev(v)∈S。故这里也有 prev ( u ) ∈ S \text{prev}(u)\in S prev(u)∈S。将 prev ( u ) \text{prev}(u) prev(u)作为 u u u,由同样的思路可得 prev ( prev ( u ) ) ∈ S \text{prev}(\text{prev}(u))\in S prev(prev(u))∈S。不断迭代,可得 s , ? ? , prev ( prev ( u ) ) , prev ( u ) ∈ S s,\cdots,\text{prev}(\text{prev}(u)),\text{prev}(u)\in S s,?,prev(prev(u)),prev(u)∈S。?
引理2 满足 d ( u ) = min ? v ∈ V ? S d ( v ) d(u)=\min\limits_{v\in V-S}d(v) d(u)=v∈V?Smin?d(v)的顶点 u u u一定有 d ( u ) = δ ( u ) d(u)=\delta (u) d(u)=δ(u)。
证明:
归纳基础:当 S = ? S=\empty S=?时, d ( s ) = 0 d(s)=0 d(s)=0,故一定会选择 u = s u=s u=s,且 d ( s ) = δ ( s ) = 0 d(s)=\delta(s)=0 d(s)=δ(s)=0成立。
归纳步:设对于 S = S k S=S_k S=Sk?时,结论成立,即 ? v ∈ S \forall v\in S ?v∈S有 d ( v ) = δ ( v ) d(v)=\delta(v) d(v)=δ(v);要证对于 S = S k + 1 = S ∪ { u } S=S_{k+1}=S\cup\{u\} S=Sk+1?=S∪{u}时结论也成立,其中 u u u满足 d ( u ) = min ? v ? S k , v ∈ V d ( v ) d(u)=\min\limits_{v\notin S_k,v\in V}d(v) d(u)=v∈/?Sk?,v∈Vmin?d(v)。也就是证明 d ( u ) = δ ( u ) d(u)=\delta(u) d(u)=δ(u)。
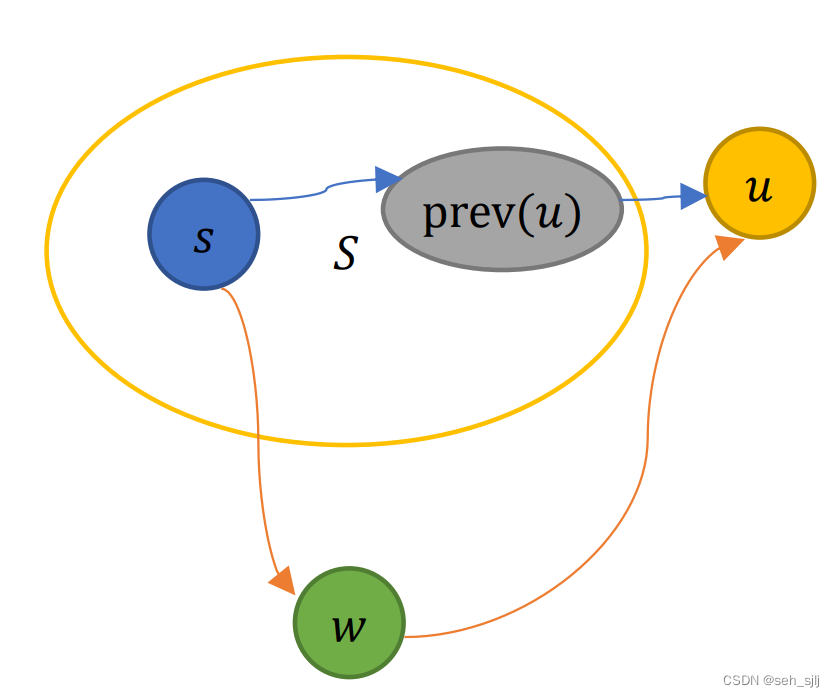
我们认为 Γ ( u ) = ( s , ? ? , prev ( prev ( u ) ) , prev ( u ) , u ) \Gamma(u)=(s,\cdots,\text{prev}(\text{prev}(u)),\text{prev}(u),u) Γ(u)=(s,?,prev(prev(u)),prev(u),u)是 s s s到 u u u的最短路径。我们需要证明不存在更短的路径 Γ ′ ( u ) \Gamma'(u) Γ′(u)。首先,根据归纳假设,有 d ( prev ( u ) ) = δ ( prev ( u ) ) d(\text{prev}(u))=\delta(\text{prev}(u)) d(prev(u))=δ(prev(u))。而根据算法的步骤有 d ( u ) = min ? p ∈ S { d ( p ) + w ( p , u ) } d(u)=\min\limits_{p\in S}\{d(p)+w(p,u)\} d(u)=p∈Smin?{d(p)+w(p,u)},因此若存在更短的路径 Γ ′ \Gamma' Γ′,在 Γ ′ \Gamma' Γ′中除了 u u u以外一定还有不属于 S S S的节点。设从 Γ ′ \Gamma' Γ′上 s s s到 u u u的第一个不属于 S S S的节点是 w w w,则 d ( w ) ≤ d ( u ) d(w)\le d(u) d(w)≤d(u),这与 u u u满足 d ( u ) = min ? v ? S k , v ∈ V d ( v ) d(u)=\min\limits_{v\notin S_k,v\in V}d(v) d(u)=v∈/?Sk?,v∈Vmin?d(v)矛盾,故假设不成立, Γ \Gamma Γ就是 s s s到 u u u的最短路径。?
换言之,将
u
u
u取为
V
?
S
V-S
V?S中
d
d
d最小的节点保证了
u
u
u的前驱节点一定在
S
S
S中。由于
S
S
S中节点的
δ
\delta
δ都是确定的,且
u
u
u是
V
?
S
V-S
V?S中离
S
S
S最近的节点,则
u
u
u的
δ
\delta
δ值是
V
?
S
V-S
V?S中最小的,但比
S
S
S中任何节点的
δ
\delta
δ值要大。
由引理2,我们令
S
=
V
S=V
S=V可得
?
u
∈
V
,
d
(
u
)
=
δ
(
u
)
\forall u\in V,d(u)=\delta(u)
?u∈V,d(u)=δ(u)。因此Dijkstra算法是正确的。
代码实现
伪代码:
Dijkstra(Graph G(V, E), Node s) // s为源点
{
?u∈V: d[u] = +∞, vis[u] = false // 初始化
// d就是已经求出的距离,vis表示u是否在集合S中
d[s] = 0
while(S != V)
{
u = V - S中d最小的节点
vis[u] = true
S = S ∪ {u}
for(每条以u为起始的边e)
{
v = e的终点
if(d[v] > d[u] + w(e))
{
d[v] = d[u] + w(e)
prev[v] = u // 设置v的前驱节点为u
}
}
}
}
如果采用堆进行优化,在每次d[v]被更新时执行DecreaseKey操作,就可以将复杂度将为
O
(
m
log
?
n
)
O(m\log n)
O(mlogn)。但是C++的priority_queue不支持DecreaseKey,所以需要每次将节点v及其距离d[v]同时放入priority_queue中,使得复杂度升为
O
(
m
log
?
m
)
O(m\log m)
O(mlogm)。
C++代码:
int dis[MAXN]; // d数组
bool vis[MAXN]; // 节点是否在S中
struct node
{
int u, d;
bool operator<(const node& o) const
{
return d > o.d; // 为了维持小根堆的性质,重载运算符
}
};
void Dijkstra(int s)
{
memset(dis, 0x3f, sizeof(dis)); // dis置为正无穷
dis[s] = 0;
priority_queue<node> Q; // 堆
Q.push({s, 0}); // 一开始S={s}
while(!Q.empty())
{
int u = Q.top().u;
Q.pop();
if(vis[u]) continue;
/* 因为priority_queue不支持DecreaseKey,
每次dis[v]被更新时都要加入堆中,使得同一个v会在堆中出现多次*/
vis[u] = true;
for(int e = first[u]; e; e = nxt[e])
{
int v = go[e];
if(dis[v] > dis[u] + val[e])
// 根据引理2,此时vis[v]一定为false,因为S中的节点最短路长度不可能再被更新
{
dis[v] = dis[u] + val[e]; // 松弛操作
Q.push({v, dis[v]}); // 加入堆中
}
}
}
}
三、Floyd-Warshall算法
基本思想
采用邻接矩阵存图。 w ( i , j ) w(i,j) w(i,j)表示点 i , j i,j i,j之间的边权, f ( i , j ) f(i,j) f(i,j)表示 i , j i,j i,j之间的最短路径。假设节点从 1 1 1到 n n n编号。
初始化 f ( i , j ) = { 0 , i = j + ∞ , ( i , j ) ? E w ( i , j ) , ( i , j ) ∈ E f(i,j)=\begin{cases}0,&i=j\\+\infty,&(i,j)\notin E\\w(i,j),&(i,j)\in E\end{cases} f(i,j)=??????0,+∞,w(i,j),?i=j(i,j)∈/?E(i,j)∈E?并设点集 S S S表示某两点间路径上可能包含的中间点的集合,初始状态为 S = ? S=\emptyset S=?。
将 k k k从 1 1 1循环到 n n n。对于每一个 k k k,当前的 S = { 1 , 2 , ? ? , k ? 1 } S=\{1,2,\cdots, k-1\} S={1,2,?,k?1},而 f ( i , j ) f(i,j) f(i,j)这里表示从 i i i到 j j j只经过集合 S S S中的点的最短路径。此时我们将 k k k并入集合 S S S,并令 f ( i , j ) = min ? ( f ( i , j ) , ? f ( i , k ) + f ( k , j ) ) f(i,j)=\min(f(i,j),\ f(i,k)+f(k,j)) f(i,j)=min(f(i,j),?f(i,k)+f(k,j))。到最后 k = n k=n k=n时, S = V S=V S=V,那么 i i i到 j j j的只经过 S S S中的节点的最短路径 f ( i , j ) f(i,j) f(i,j)就是 i i i到 j j j的最短路径了。
正确性证明
归纳假设:对于每一个 k k k,当 k k k并入 S S S后 f ( i , j ) f(i,j) f(i,j)就是从 i i i到 j j j只经过 S = { 1 , 2 , ? ? , k } S=\{1,2,\cdots,k\} S={1,2,?,k}中的节点的最短路径。
归纳基础:当 k = 0 k=0 k=0时, f ( i , j ) = { 0 , i = j + ∞ , ( i , j ) ? E w ( i , j ) , ( i , j ) ∈ E f(i,j)=\begin{cases}0,&i=j\\+\infty,&(i,j)\notin E\\w(i,j),&(i,j)\in E\end{cases} f(i,j)=??????0,+∞,w(i,j),?i=j(i,j)∈/?E(i,j)∈E?显然就是从 i i i到 j j j不经过任何中间节点的最短路径。
归纳步:假设对于 k ? 1 k-1 k?1时成立,即:在进行第 k k k步之前 f ( i , j ) f(i,j) f(i,j)是从 i i i到 j j j只经过 { 1 , 2 , ? ? , k ? 1 } \{1,2,\cdots,k-1\} {1,2,?,k?1}中的节点的最短路径。则当 k k k加入 S S S中后, f ( i , j ) f(i,j) f(i,j)分两种情况:
(1) 从
i
i
i到
j
j
j只经过
S
=
{
1
,
2
,
?
?
,
k
}
S=\{1,2,\cdots,k\}
S={1,2,?,k}中节点的最短路径不经过节点
k
k
k,则
f
(
i
,
j
)
f(i,j)
f(i,j)不改变。
(2) 经过节点
k
k
k。设集合
S
=
{
1
,
2
,
?
?
,
k
}
S=\{1,2,\cdots,k\}
S={1,2,?,k}的导出子图为
G
k
G_k
Gk?,则
f
(
i
,
j
)
f(i,j)
f(i,j)就是
G
k
G_k
Gk?中从
i
i
i到
j
j
j的最短路径。在
G
k
G_k
Gk?中应用最短路的最优子结构性质,得知
i
i
i到
j
j
j经过
k
k
k的最短路就是
i
i
i到
k
k
k的最短路连上
k
k
k到
j
j
j的最短路。因此
f
(
i
,
j
)
=
f
(
i
,
k
)
+
f
(
k
,
j
)
f(i,j)=f(i,k)+f(k,j)
f(i,j)=f(i,k)+f(k,j)。
将 f ( i , j ) 与 f ( i , k ) + f ( k , j ) f(i,j)与f(i,k)+f(k,j) f(i,j)与f(i,k)+f(k,j)作比较取较小者,就可以知道最短路是否经过 k k k。?
代码实现
时间复杂度 O ( n 3 ) O(n^3) O(n3)。
memset(f, 0x3f, sizeof(f)); // f先全部置为正无穷
for(int i = 1; i <= n; ++i)
for(int j = 1; j <= n; ++j)
f[i][j] = read(); // 读入邻接矩阵
for(int k = 1; k <= n; ++k)
for(int i = 1; i <= n; ++i)
for(int j = 1; j <= n; ++j)
f[i][j] = min(f[i][j], f[i][k] + f[k][j]);
