2276. 统计区间中的整数数目
给你区间的 空 集,请你设计并实现满足要求的数据结构:
- 新增:添加一个区间到这个区间集合中。
- 统计:计算出现在 至少一个 区间中的整数个数。
实现 CountIntervals 类:
CountIntervals() 使用区间的空集初始化对象
void add(int left, int right) 添加区间 [left, right] 到区间集合之中。
int count() 返回出现在 至少一个 区间中的整数个数。
注意:区间 [left, right] 表示满足 left <= x <= right 的所有整数 x 。
示例 1:
输入: [“CountIntervals”, “add”, “add”, “count”, “add”, “count”] [[], [2,3], [7, 10], [], [5, 8], []]
输出: [null, null, null, 6, null, 8]解释:
CountIntervals countIntervals = new CountIntervals(); //用一个区间空集初始化对象
countIntervals.add(2, 3); // 将 [2, 3] 添加到区间集合中
countIntervals.add(7, 10); // 将 [7, 10] 添加到区间集合中
countIntervals.count(); // 返回 6 ; 整数 2 和 3 出现在区间 [2, 3] 中 ; 整数 7、8、9、10 出现在区间 [7, 10]
countIntervals.add(5, 8); // 将 [5, 8] 添加到区间集合中
countIntervals.count(); // 返回 8 ; 整数 2 和 3 出现在区间 [2, 3] 中
// 整数 5 和 6 出现在区间 [5, 8] 中
// 整数 7 和 8 出现在区间 [5, 8] 和区间 [7, 10] 中
// 整数 9 和 10 出现在区间 [7, 10] 中
提示:
- 1 <= left <= right <= 1e9
- 最多调用 add 和 count 方法 总计 1e5 次
- 调用 count方法至少一次
解析
- 相当于区间合并,每次记录区间插入之后区间长度的变化。
- 每次区间插入,需要找到插入点的位置,使用set<pair<int,int>> 存储每个区间。
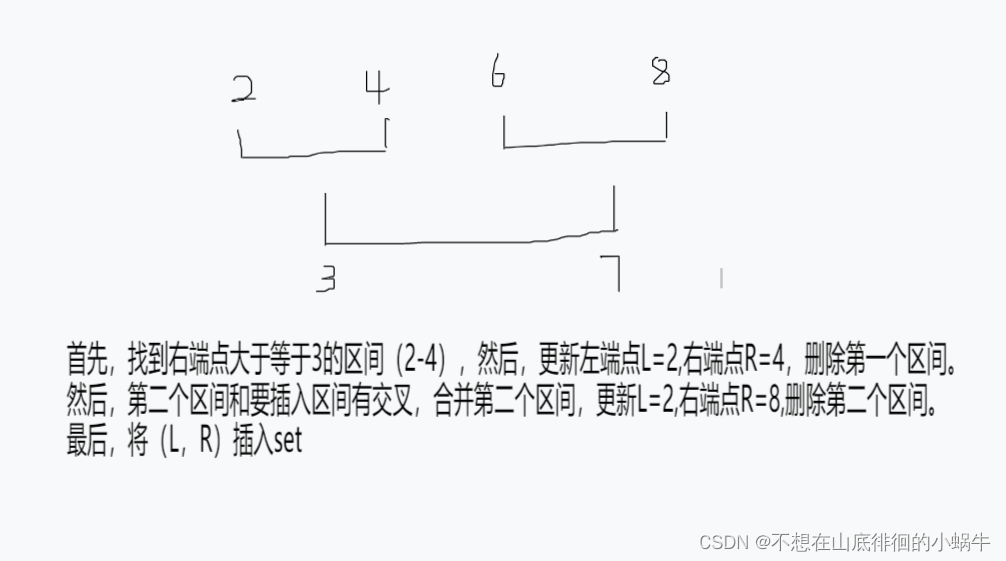
- set按照右区间排序,首先要找到set中第一个要合并的区间(第一个区间的右端点要大于等于要插入区间的左端点),后边区间逐个合并,直到要插入区间的右端点小于等于set中区间的左端点。
- 合并的过程中只需要记录下来已经合并的最左端,最右端即可,合并完的区间直接删除,最后将新区间(L,R)插入。
- 需要根据右端点排序,每次找到需要插入的点要根据右端点寻找。
code
class CountIntervals {
typedef pair<int,int> pii;
set<pii> se;
int ans=0;
public:
CountIntervals() {
}
void add(int left, int right) {
// 记录要插入的左右端点
int L=left,R=right;
// 找到一个要插入的点
// 之所以要使用left-1,right+1是想要将
//2 3 ,4 6 ,7 8这样相邻区间合并到一起
//(如果是求区间个数的话需要这样合并,本题也可以不用)
// (如果求区间长度也不可以用left-1,right+1)
auto it=se.lower_bound(pii(left-1,-2e9));
while(it!=se.end()){
// 如果左端点大于要插入的右端点了
// 当前为4 6,插入的为1 3,这时候就不用看4 6 了直接break
if(it->second>right+1) break;
L=min(L,it->second);
R=max(R,it->first);
ans-=it->first-it->second+1;
se.erase(it++);
}
// 合并的区间插入(需要先按照right,后left排序)
se.insert(make_pair(R,L));
ans+=R-L+1;
}
int count() {
return ans;
}
};
/**
* Your CountIntervals object will be instantiated and called as such:
* CountIntervals* obj = new CountIntervals();
* obj->add(left,right);
* int param_2 = obj->count();
*/
