[数据结构与算法]C++ STL中的sort源码浅析

首先提出几个问题：

C++ STL默认提供以下两个sort接口

void std::sort(const _RanIt _First, const _RanIt _Last)
void std::sort(const _RanIt _First, const _RanIt _Last, _Pr _Pred)

第一个函数的参数是排序区间，第二个函数的参数是排序区间和指定排序方式的函数对象

C++ STL默认使用less函数对象，进行升序排序

template <class _RanIt>
_CONSTEXPR20 void sort(const _RanIt _First, const _RanIt _Last) { // order [_First, _Last)
    _STD sort(_First, _Last, less<>{});
}

而实际上，对外提供的两个sort接口，最后调用的都是三个参数的这个sort接口，该接口源码如下：

template <class _RanIt, class _Pr>
_CONSTEXPR20 void sort(const _RanIt _First, const _RanIt _Last, _Pr _Pred) { // order [_First, _Last)
    _Adl_verify_range(_First, 	_Last);                // 检查区间合法性
    const auto _UFirst = _Get_unwrapped(_First);
    const auto _ULast  = _Get_unwrapped(_Last);
    _Sort_unchecked(_UFirst, _ULast, _ULast - _UFirst, _Pass_fn(_Pred));
}

主要调用的就是_Sort_unchecked函数

void _Sort_unchecked(_RanIt _First, _RanIt _Last, _Iter_diff_t<_RanIt> _Ideal, _Pr _Pred)

• _First：首元素的迭代器
• _Last：末尾元素后继位置的迭代器
• _Ideal：_Sort_unchecked会递归调用，_Ideal的初始值是排序区间的元素个数，每次递归都会减小，用于控制递归层数
• _Pred：指定排序方式的函数对象

_Sort_unchecked函数源码如下：

template <class _RanIt, class _Pr>
_CONSTEXPR20 void _Sort_unchecked(_RanIt _First, _RanIt _Last, _Iter_diff_t<_RanIt> _Ideal, _Pr _Pred) {
    // order [_First, _Last)
    for (;;) {
        if (_Last - _First <= _ISORT_MAX) { // small
            _Insertion_sort_unchecked(_First, _Last, _Pred);
            return;
        }

        if (_Ideal <= 0) { // heap sort if too many divisions
            _Make_heap_unchecked(_First, _Last, _Pred);
            _Sort_heap_unchecked(_First, _Last, _Pred);
            return;
        }

        // divide and conquer by quicksort
        auto _Mid = _Partition_by_median_guess_unchecked(_First, _Last, _Pred);

        _Ideal = (_Ideal >> 1) + (_Ideal >> 2); // allow 1.5 log2(N) divisions

        if (_Mid.first - _First < _Last - _Mid.second) { // loop on second half
            _Sort_unchecked(_First, _Mid.first, _Ideal, _Pred);
            _First = _Mid.second;
        } else { // loop on first half
            _Sort_unchecked(_Mid.second, _Last, _Ideal, _Pred);
            _Last = _Mid.first;
        }
    }
}

元素少，使用插入排序

// _INLINE_VAR constexpr int _ISORT_MAX = 32; // maximum size for insertion sort
if (_Last - _First <= _ISORT_MAX) { // small
    _Insertion_sort_unchecked(_First, _Last, _Pred);
    return;
}

首先判断排序区间的元素个数是否不足_ISORT_MAX，这个_ISORT_MAX默认是32，如果元素个数不够，就调用插入排序算法完成排序，并退出程序

由于算法主体还是使用快速排序，快速排序会把小的元素往左调整，大的元素往右调整，随着快速排序的进行，元素会逐渐趋于有序。而对于趋于有序的序列，插入排序的效率是最高的（排某个元素的时候只需要比较很少的次数）

递归次数过多，使用堆排序

if (_Ideal <= 0) { // heap sort if too many divisions
    _Make_heap_unchecked(_First, _Last, _Pred);
    _Sort_heap_unchecked(_First, _Last, _Pred);
    return;
}

由于_Sort_unchecked会递归调用，_Ideal的初始值是排序区间的元素个数，为了控制递归层数，每次递归都会以如下方式减小：

_Ideal = (_Ideal >> 1) + (_Ideal >> 2);

算法主体还是使用快速排序，当快排递归为一单边树导致递归次数过多时，为避免栈溢出和效率低下的问题，_Ideal的值会减小为0。接着就会用堆排序的方式对剩余区间的元素进行排序（堆排序时间复杂度稳定为$O(lo{g}_{2}n)$，而且不占用额外的空间）

虽然归并排序的时间复杂度也是$O(lo{g}_{2}n)$，但会占用额外的内存空间，源码上还是选择堆排序

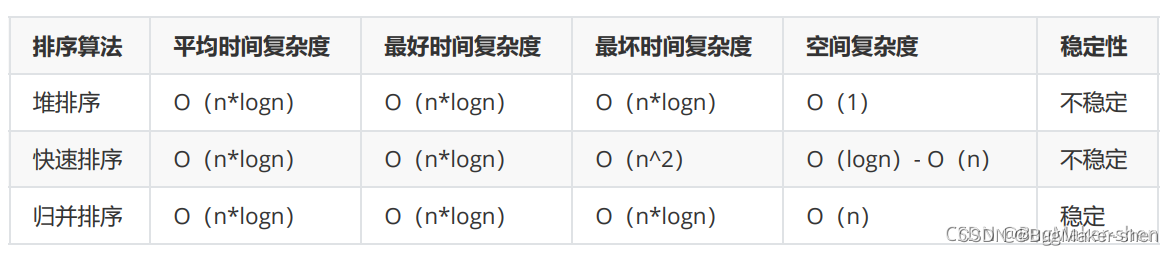
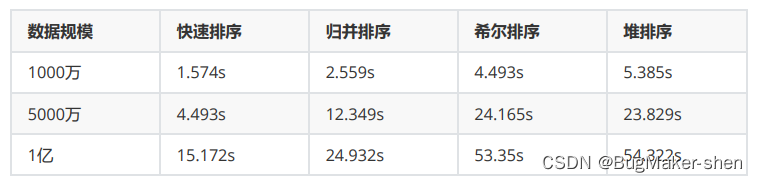
当递归层数较深时，待排区间内元素也不会很多了，在数据量较小的情况下，堆排和归并排序效率相当

主体使用快速排序

// divide and conquer by quicksort
auto _Mid = _Partition_by_median_guess_unchecked(_First, _Last, _Pred);

_Ideal = (_Ideal >> 1) + (_Ideal >> 2); // allow 1.5 log2(N) divisions

if (_Mid.first - _First < _Last - _Mid.second) { // loop on second half
    _Sort_unchecked(_First, _Mid.first, _Ideal, _Pred);
    _First = _Mid.second;
} else { // loop on first half
    _Sort_unchecked(_Mid.second, _Last, _Ideal, _Pred);
    _Last = _Mid.first;
}

最后一段，先调用快速排序，然后根据返回的_Mid，判断下次递归排序的区间，再调用_Sort_unchecked

总结

1. STL里sort算法用的是什么排序算法？
   主要使用快速排序；区间元素少于32时，使用插入排序；快排的递归次数过多，使用堆排序

2. 快速排序的时间复杂度不是稳定的$O(nlo{g}_{2}n)$，最坏情况会变成$O(n^2)$，怎么解决复杂度恶化问题?
   快速排序不是稳定的O(log2n)，最坏的情况会变成O(n^2)，可以通过 改插入排序 或者 三数取中 的方法改善情况恶化

3. 递归过深会引发什么问题？
   递归太深可能导致函数调用开销过多，甚至栈溢出，程序崩溃

4. 怎么控制递归深度？如果达到递归深度了还没排完序怎么办?
   快速排序复杂度恶化时，递归会很深，STL的sort中有一个变量_Ideal，每递归深入一次，_Ideal就会减小，当_Ideal为0时，就会调用稳定$O(nlo{g}_{2}n)$的非递归堆排序。此外还会判断当前区间的排序元素个数，少于32时，会转入插入排序，这也能防止递归次数过多导致复杂度恶化

创作打卡挑战赛

赢取流量/现金/CSDN周边激励大奖