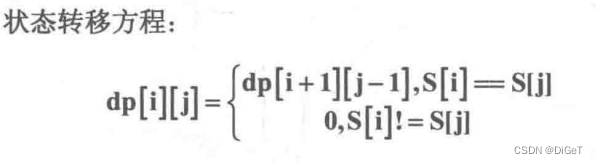198. 打家劫舍
题意:偷钱,且不能偷相邻的。
思路:动态规划
nums[i]表示第i家存放的金额,dp[i]表示偷第i家时能获得的最高金额,
其中dp[0]=nums[0],dp[1]=nums[1],dp[2]=dp[0]+arr[2],dp[3]=Max(dp[0],dp[1]) + nums[3],dp[3]之后都是如此。
也就是说当i>2时,偷第i家时能获得的最高金额取决于在i-2家或i-3家中所能偷到的最高金额,即dp[i]=Max(dp[i-2],dp[i-3]) + nums[i]。
由于计算dp[i]数组时,我们需要用到nums[i]数组,但和那些小于i的nums数据没关系,也就是可以不保留,所以可用nums数组代替dp数组。
一开始不理解也正常,都是从简单到复杂,不断优化。可能我这里呈现了很简练的代码,但并不代表这是我一开始就能写出来的。
class Solution {
public int rob(int[] nums) {
int len=nums.length;
int max=0;
for(int i=0;i<len;i++){
if(i==2){
nums[i]+=nums[i-2];//i=2的情况
}else if(i>2){
nums[i]+= Math.max(nums[i-2],nums[i-3]);
}
if(max<nums[i]) max=nums[i];//记录最大值,包括了i=0和1的情况
}
return max;
}
}
213. 打家劫舍 II
题意:偷钱,且不能偷相邻的,附加条件:第一家和最后一家是相邻的。
思路:动态规划
附加条件,导致动态规划偷最后一家时,不知道前面的是否偷了第一家。我们可以调用两次动态规划避免该问题,即[0, len-2]和[1,len-1],这样就保证第一家和最后一家不会同时被偷。
注意调用两次,如果把nums作为dp数组第一次会修改nums,所以不能,但可以用临时变量代替,观察dp[i]=Max(dp[i-2],dp[i-3]) + nums[i],每次计算dp[i],需要dp[i-2] (dp_2),dp[i-3] (dp_3),也需要dp[i-1] (dp_1)==>用于下一次,使用临时变量并没有下标,只有保存dp[i-1],才能在下次更新dp_2和dp_3,不然根本没法移动。
?? 动态规划的公式不一定唯一,例如官方解答代码更简洁
class Solution {
public int rob(int[] nums) {
int len =nums.length;
return Math.max(solve(0,len-2,nums),solve(1,len-1,nums));
}
private int solve(int idx, int l, int[] nums){
int max = nums[0]; //防止只有一个 例如[1]
int dp_2=0, dp_3=0, dp_1=0; //补零,特殊值处理(这样每个数都符合dp[i]=Max(dp[i-2],dp[i-3]) + nums[i])
for(int i=idx; i<=l; i++) {
int tmp = Math.max(dp_2, dp_3) + nums[i];
dp_3 = dp_2;
dp_2 = dp_1;
dp_1 = tmp;
if(max < tmp) max = tmp;
}
return max;
}
}
5. 最长回文子串
思路一:字符串中心扩展(双指针)
以字符为中心,不断向外扩展,比较左右是否相等,中间记录下最长串就行了。例如:aba
①遇到a,以a为中心,发现a左边越界,结束;
②遇到b,以b为中心,b的左右都不越界且相等,跟最大值(0)比较,大于则更新最大值,并记录串的位置,即start=0,end=2,继续扩展,发现越界,结束。
③遇到a,同理①。结果最大串为substring(start,end)
当然,我们还需要以两个字符为中心进行扩展。例如对于abba,如果以上面的例子,即一个字符为中心进行扩展,则结果为1,但实际结果为4
class Solution {
public String longestPalindrome(String s) {
//中心扩展
int len = s.length();
int start=0, end=0; //记录最大串的开始和结束下标
int max=0; //记录最大的串
for(int i=0; i<len; i++) {
int l = i-1, r=i+1;
//以单个数进行中心扩展---例如"ababa"
while(l>=0 && r<len) {
if(s.charAt(l) != s.charAt(r)) break;
if(r-l>max) {
start=l;
end=r;
max=r-l;
}
l--;
r++;
}
//以两数进行中心扩展----例如"cbbd"
l=i;
r=i+1;
while(l>=0 && r<len) {
if(s.charAt(l) != s.charAt(r)) break;
if(r-l>max) {
start=l;
end=r;
max=r-l;
}
l--;
r++;
}
}
return s.substring(start, end+1);
}
}
优化:单数和双数的中心扩展代码可抽取为方法
思路二:动态规划
外扩的方式,
class Solution {
public String longestPalindrome(String s) {
int l = s.length();
int[][] dp = new int[l][l];
for (int i = 0; i < l; i++) { //长度为1
dp[i][i] = 1;
}
int start = 0, end = 0; //记录最长字串下标——最后一次的记录必定最长(思考)
for (int len = 2; len <= l; len++) { //遍历长度为2、长度为3、长……
int k = l - len;
for (int i = 0; i <= k; i++) {
int j = i + len - 1; //串尾
if (s.charAt(i) == s.charAt(j)) {
if (len == 2 || dp[i + 1][j - 1] == 1) { //长度为2的需要特殊处理
dp[i][j] = 1;
start = i;
end = j;
}
}
}
}
return s.substring(start, end + 1);
}
}
343. 整数拆分
思路:动态规划
2=1×1 ——max=1
3=1×2 ——max=2
4=1×3 或 2×2 ——max=4
5=1×4 或 2×3 ——max=6
6=1×5 或 2×4 或 3×3 ——max=9 ==>双指针即可遍历每个数的不同拆分。
当然,这里只是拆分为两个数,所以还需要动态规划来帮我们获取更细的拆分。用dp[i]表示整数 i 所能拆分后所能获得的最大乘积。其中,dp[1]=1,dp[2]=1。例如6=1×5,如果dp[5]大于5,则说明5需要拆分,用dp[5]替换5。其中,计算dp[6]时,dp[5]肯定是前面先算好了。
class Solution {
public int integerBreak(int n) {
int[] dp = new int[n + 1];
dp[1] = 1; //初始化
dp[2] = 1;
for (int i = 3; i <= n; i++) {
int l = 1, r = i-l; //双指针
while (l <= r) {
//判断是否需要拆分
int tmp = Math.max(l, dp[l]) * Math.max(r, dp[r]);
//更新最大值
if (tmp > dp[i]) dp[i] = tmp;
l++;
r--;
}
}
return dp[n];
}
}
279. 完全平方数
思路:动态规划
获取1-n这些数所需完全平方数的最少数量,用dp[i]表示
dp[1] = dp[1-0] + 1 dp[2] = dp[2-1] + 1 数量加一代表减去的那个平方数
dp[3] = dp[3-1] + 1 dp[4] = dp[4-1] + 1 或者 dp[4-4] + 1
dp[i] = dp[i-pft] + 1 pft是小于等于i的完全平方数,从1开始算 1*1 2*2 3*3
动态方程:dp[i] = Math.min(dp[i], dp[i-pft]+1) 有多个解,需要判断是否比原来的更优
class Solution {
public int numSquares(int n) {
int[] dp = new int[n + 1];
for (int i = 1; i <= n; i++) {
dp[i] = i; //初始化最坏的情况,全是1
for (int j = 1; j * j <= i; j++) {
dp[i] = Math.min(dp[i], dp[i - j * j] + 1);
}
}
return dp[n];
}
}