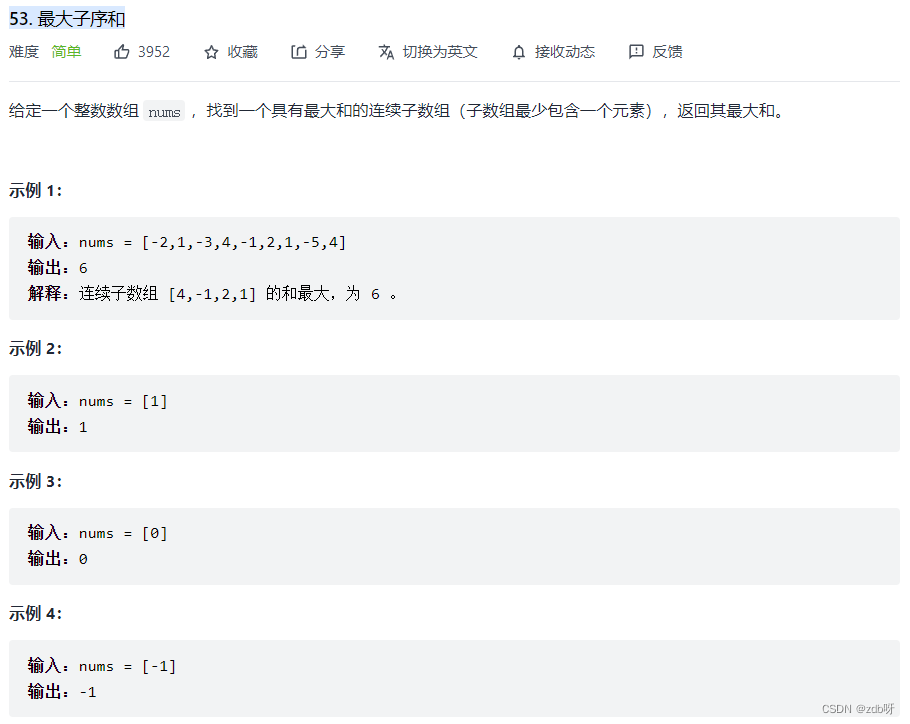
53. 最大子数组和【简单】
你一定会想计算每一个索引开头的最大子序和吧!

那就写出第一种方法:
思路一:双for循环暴力破解:计算从每一个索引开始的最大子序和
- 第一个for遍历每个子序和开头的索引
- 第二个for记录遍历到的元素,在里面收集更新结果
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int res = INT_MIN;
for(int i = 0; i < nums.size(); ++i){
int temp = 0;
for(int j = i; j < nums.size(); ++j){
temp += nums[j]; //当前的累积和
res = max(res, temp); //更新最大值
}
}
return res;
}
};
结果就不用我说了吧

哪还有什么方法呢?

我们可以随着遍历生成一个数组,这个数组记录当前的子序和最大值
思路二:动态规划
class Solution {
public:
int maxSubArray(vector<int>& nums) {
//先替换元素 更新数组
for (int i = 1; i < nums.size(); i++) {
if (nums[i - 1] > 0) { //如果前一个元素>0 后一个元素改为两者之和
nums[i] = nums[i - 1] + nums[i]; //新生成的记录当前的子序和最大值的数组
}
}
//再遍历查找最大值
int res = nums[0];
for (int i : nums) {
res = max(res, i);
}
return res;
}
};
我们可以对两个并行for循环进行优化,只用一个for循环解决
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int res = nums[0];
for (int i = 1; i < nums.size(); i++) {
if (nums[i - 1] > 0) {
nums[i] = nums[i - 1] + nums[i];
}
if (nums[i] > res) {
res = nums[i];
}
}
return res;
}
};
接着优化缩短代码,美化程序
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int res = nums[0];
for (int i = 1; i < nums.size(); i++) {
nums[i] = max(0 + nums[i], nums[i - 1] + nums[i]); //主要是这句代码
res = max(res, nums[i]); //动态记录最大子序和
}
return res;
}
};
时间复杂度:O(n)
空间复杂度:O(1)
怎么样?会难吗
