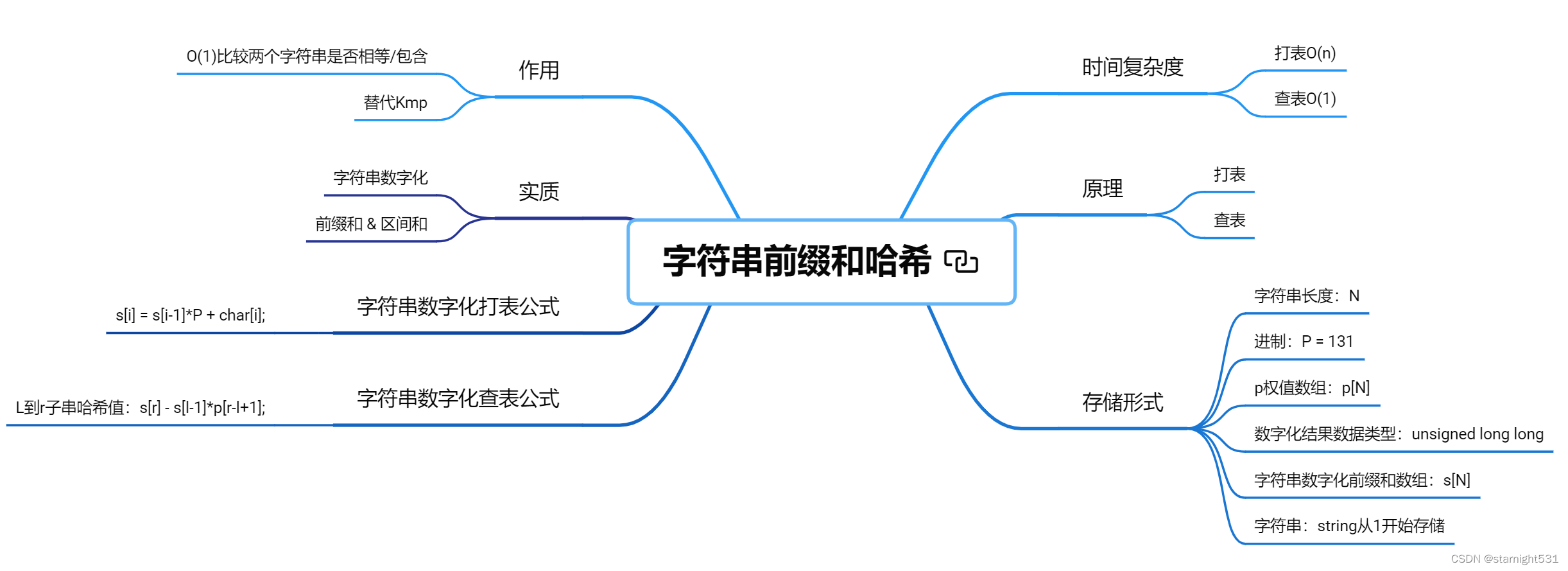
字符串前缀哈希
食用指南:
对该算法程序编写以及踩坑点很熟悉的同学可以直接跳转到代码模板查看完整代码
只有基础算法的题目会有关于该算法的原理,实现步骤,代码注意点,代码模板,代码误区的讲解
非基础算法的题目侧重题目分析,代码实现,以及必要的代码理解误区
题目描述:
-
给定一个长度为 n 的字符串,再给定 m 个询问,每个询问包含四个整数 l1,r1,l2,r2,请你判断 [l1,r1] 和 [l2,r2] 这两个区间所包含的字符串子串是否完全相同。
字符串中只包含大小写英文字母和数字。输入格式
第一行包含整数 n 和 m,表示字符串长度和询问次数。
第二行包含一个长度为 n 的字符串,字符串中只包含大小写英文字母和数字。
接下来 m 行,每行包含四个整数 l1,r1,l2,r2,表 示一次询问所涉及的两个区间。
注意,字符串的位置从 1 开始编号。输出格式
对于每个询问输出一个结果,如果两个字符串子串完全相同则输出 Yes,否则输出 No。
每个结果占一行。数据范围
1≤n,m≤105
输入样例:
8 3
aabbaabb
1 3 5 7
1 3 6 8
1 2 1 2
输出样例:
Yes
No
Yes -
题目来源:https://www.acwing.com/problem/content/843/
题目分析:
-
题干浓缩:给定字符串,m次询问,求确定每次[L1, R1] 和 [L2, R2]的子串是否相等
这个题干和给定序列求区间和的问法相同 -
暴力:
针对每次询问
当子串长度都不相等时,必然两串不等,O(1)
当子串长度相等时,遍历子串,最坏O(n)整体最坏时间复杂度:O(mn),1010,十亿,严重超时
-
前缀和哈希:
为字符串每个前缀子串(以string第一个字母开头的子串)建立前缀和数组
利用前缀和的区间公式,可以计算出任一子串的唯一哈希值,通过查看哈希值是否相等即可完成比较
打表O(n),查表O(1),最差十万,轻松通过看不懂不要紧,下面介绍字符串前缀哈希算法
算法原理:
模板算法:
字符串前缀和哈希:
1. 字符串数字化:
-
将字符串看作一个P进制的数
由于ASCII表中共有256个字符,但是可以显示在显示器上的只有128个,每个字符代表一个数
所以P进制一般取131进制,或者再大点的13331进制,都不用考虑进位问题了 -
每一位字符都有权重,以及本身代表的数值
如高精度所讲,字符串高位在前,低位在后
"2987654321"中2是最高位,权重为十亿;1是最低位,权重为1ASCII码表中字符本身就有数值含义,如A是65,Z是92,a是97,z是122
-
P权值数组p[N]:
由于计算一个字符的哈希值需要数值 * 权重,所以提前把131进制的所有次幂放入数组
用到第几位的权值就直接从权值数组中取出即可
2. 字符串哈希
- 此处的哈希指的不是哈希表,不是将大数映射到小数范围内
- 而是唯一性,一个字符串数字化后得到的是一个数字,这个数字也只对应一个字符串
这个数字叫字符串的哈希值 - 字符串和哈希值一一对应的关系,保证了用数字比较两个字符串是否相等是正确可行的
3. 前缀子串数组:
- 通过字符串数字化方法,可以求得每个前缀子串的数字化表达
- 对,就是前缀和公式:
s[i] = s[i-1]*P + string[i]; - 你猜前缀和数组应该是int 还是 long long ?
其实是unsigned long long 最保险
4. 区间查询:
-
若不考虑位的权值,L到r的区间和是s[r] - s[l-1]
-
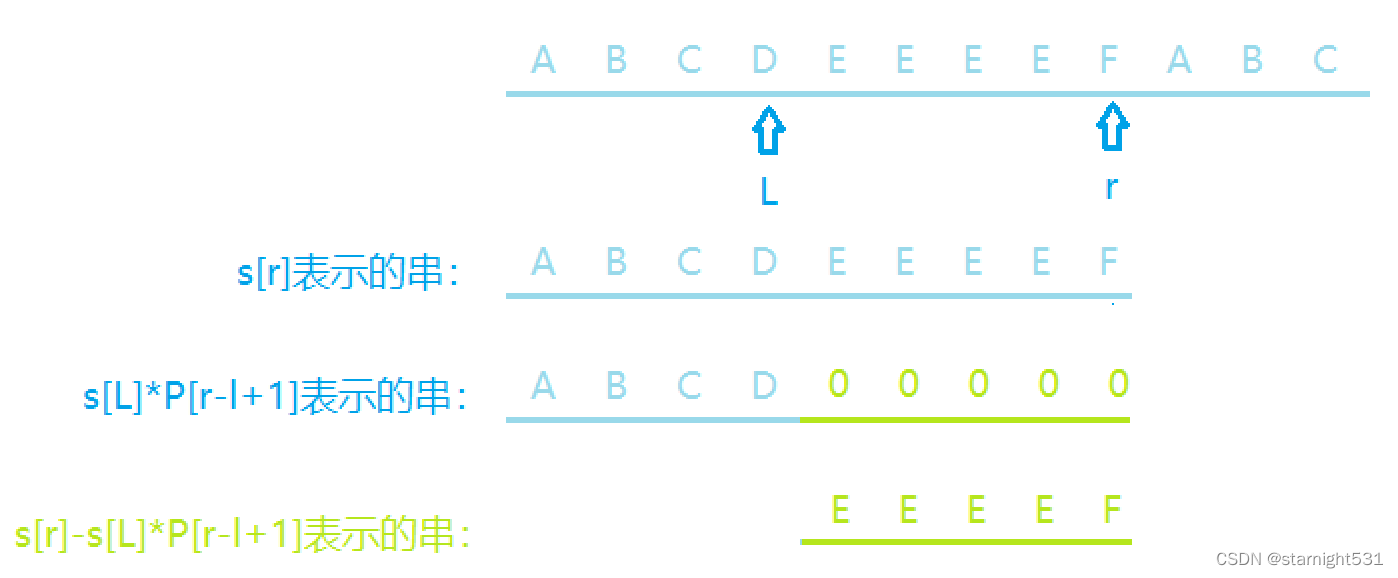
但是字符串建立前缀和时考虑了权值,L到r的区间和是 s[r] - s[l-1]*p[r-l+1]
s[i-1]*p[r-l+1]相当于左移r-l+1位,后面通过补0的方式将s[i-1]串长度拔高到了s[j]串长度
由于s[j]串后面是具体的字符,而*p[r-l+1]的s[l]串后面是0,所以两者做差得到的就是L到r的区间哈希值
写作步骤:
1. 初始化:
- 设置P进制 & p[]权值数组 & 从string[1]读入char字符串
2. 前缀字符串数字化:
- s[i]代表从string[1]到string[i]的字符串数字化结果
- 递推公式:s[i] = s[i-1] * P + string[i]的ASCII码值
3. 字符串区间数字化:
- L到r的字符串子串数字化结果:s[r] - s[l-1] * p[r-l+1];
代码实现:
//注意点1:int 和普通long long 存放不下一个字符串哈希值
typedef unsigned long long ULL;
const int N = 100010;
const int P = 131;
ULL s[N], p[N];
ULL seg_string(int l, int r){
return h[r] - h[l-1] *p[r-l+1];
}
int main(){
char str[N];
int n=0, m=0;
//注意点2:string从1开始存储,便于求前缀和
scanf("%d%d%s",&n, &m, str+1):
for(int i=1; i<= n; i++){
//注意点3:打表P权值数组&前缀数组便于求区间和
p[i] = p[i-1]*P;
//注意点4:str此处以ASCII码参与计算字符串数字化
h[i] = h[i-1]*P + str[i];
}
while(m--){
int l1, r1, l2, r2;
cin >> l1 >> r1 >> l2 >> r2;
if(seg_string(l1,r1) == seg_string(l2,r2))
cout<<"Yes"<<endl;
else
cout<<"No"<<endl;
}
}
代码误区:
1. 字符串哈希需要哈希表吗?
- 其实不需要,直接一个unsigned long long ,就可以将字符串哈希题的最值收入囊中
2. 字符串从哪开始存储?
- 为了便于求前缀和数组,我们从string + 1开始输入字符串
3. 代替KMP算法:
- KMP算法求A串是否包含B串,即B串是不是A串的连续子串,可用字符串前缀哈希代替
- 将A串和B串都数字化:
若A串中包含B串,则A中可能有length(A) - length(B)个子串是B串

通过比较这length(A) - length(B)个子串和B串的哈希值,可以知道A串中是否包含B串
时间复杂度打表O(n),遍历查找O(length(A) - length(B))
共计O(2length(A))
4. 字符串数字化的应用:
-
很多网站都是用账号密码管理,难道我们的账号和密码都是直接存储在公司的数据库里吗?
真是这样的话,恐怕黑客不需要费劲心思攻防了,直接买通公司员工把密码赋值粘贴发来就彳亍了
其实我们输入密码之后,客户端会将密码字符串进行数字化,将数字化结果发送给服务器
服务器的数据库中也是存放的数字化字符串结果
-
由于目前算力的有限,只能做到字符串到数字的数字化,不能做到给定数字还原回字符串的逆数字化
这样一来,客户端只能发送字符串,服务器只存储数字化结果,不存在拿到数据库内容转化回密码字符串的情况
-
字符串前缀哈希就是加密算法的一种,其余常用的还有md5等等
本篇感想:
-
这个算法名字挺奇怪的,直接叫字符串数字化 & 子串数字化,那作用就更明显了
-
其实没用到哈希表,但是用到了hash思想的哈希值
不要学会拉链法和开放寻址法就迫不及待手写哈希表 -
看完本篇博客,恭喜已登 《练气境-后期》
打算讲到图论进入下一境界-《筑基境》

距离登仙境不远了,加油
