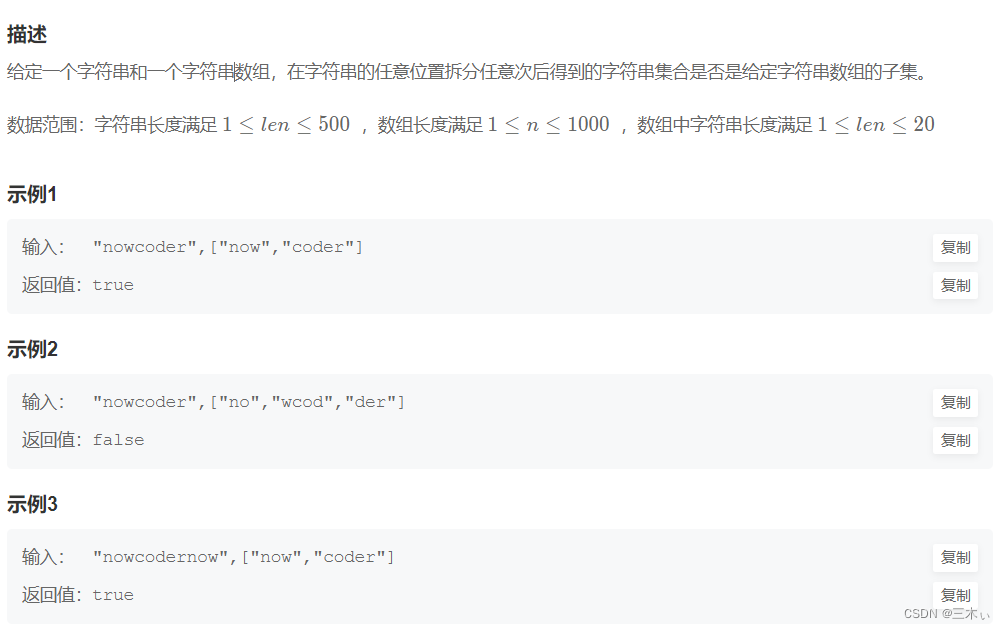
单词拆分(一)
牛客链接:NC181 单词拆分(一)
题解1:DFS
每次从字符串中从头开始选择定长的子字符串去集合中寻找对应目标,如果存在,则继续这么操作寻找后续字符串。如果找到最后,字符串为0了,那么说明字符串集合能够组成这个字符串。
class Solution {
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param s string字符串
* @param dic string字符串vector
* @return bool布尔型
*/
bool wordDiv(string s, vector<string>& dic) {
// write code here
if(s.size() == 0)
return true;
int ans = false;
for(int i =0;i<=s.size();++i){ //递归查找
string temp = s.substr(0,i);
if(find(dic.begin(), dic.end(), temp) != dic.end())
{
ans = wordDiv(s.substr(i), dic);
}
if(ans == true) //截枝
break;
}
return ans;
}
};
题解2:动态规划
设定一个dp数组,初始化为0。其中dp[i]=1表示以i结尾的字符串能够通过集合组合而成。 当前dp[i]可以通过前j个字符串和j-i字符串组合而成,如果dp[j]=1,且i-j的子字符串在集合中,则dp[i] =1;
class Solution {
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param s string字符串
* @param dic string字符串vector
* @return bool布尔型
*/
bool wordDiv(string s, vector<string>& dic) {
// write code here
unordered_set<string> us; //保所有出现过的字符串
for(string sub:dic)
us.insert(sub);
bitset<501> dp = 0; //比vector更快
dp[0] = 1;
for(int i =1;i<=s.size();++i){ //遍历之后的每一位
for(int j =0;j<i;++j){ //截取字符串长度
if(dp[j] && us.find(s.substr(j,i-j)) != us.end()) //能表示直接退出循环。
{
dp[i] = 1;
break;
}
}
}
return dp[s.size()];
}
};
单词拆分(二)
牛客链接:NC182 单词拆分(二)

解法1:DFS
深度搜索每个可能的同时,加其加入到子答案中。当s剩余0时,子答案加入答案集合,否则不成立,他不是一个子答案。
class Solution {
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param s string字符串
* @param dic string字符串vector
* @return string字符串vector
*/
void dfs(string s, string sub_ans, vector<string>& dic, vector<string> &ans){ //dfs
if(s.size() == 0){
sub_ans.erase(0, 1); //去掉开头的空格
ans.push_back(sub_ans);
return;
}
for(int i = 0;i<=s.size();++i)
{
if(find(dic.begin(),dic.end(),s.substr(0,i))!=dic.end())
{
string temp = sub_ans;
sub_ans = sub_ans +" "+s.substr(0,i);
dfs(s.substr(i), sub_ans, dic, ans);
sub_ans = temp;
}
}
}
vector<string> wordDiv(string s, vector<string>& dic) {
// write code here
vector<string> ans;
dfs(s,"",dic,ans);
return ans;
}
};
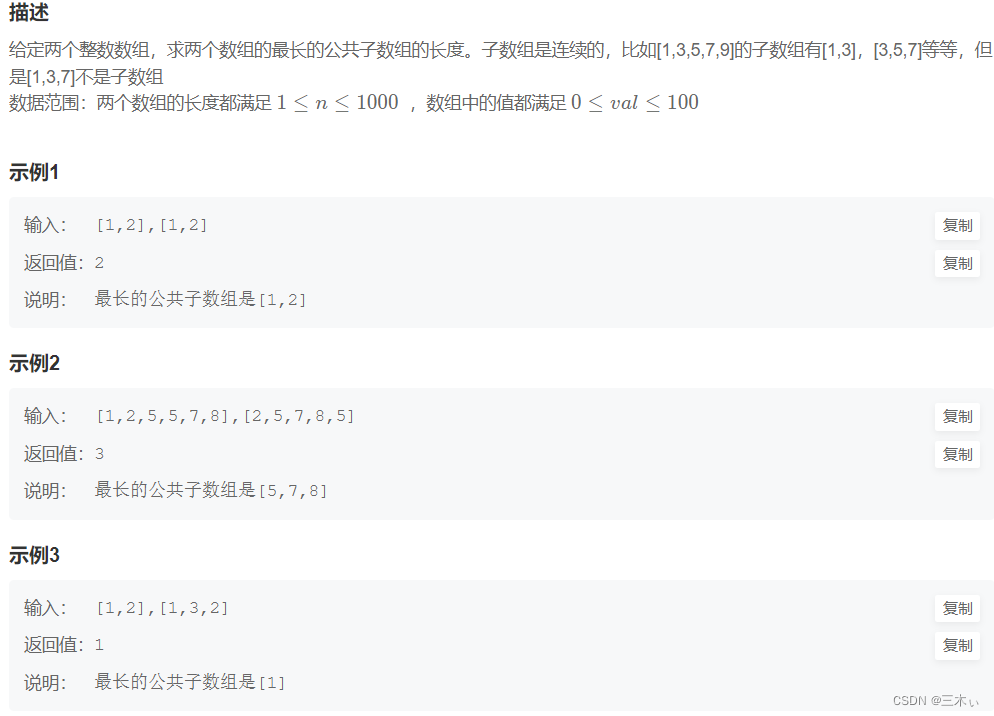
最长公共子数组
牛客链接:NC183 最长公共子数组
解法1:动态规划
定义一个二维数组ans[i][j],其中ans[i][j]表示以A中第i个元素和B中第j个元素结尾的最长后缀序列的长度,递推关系如下:
如果A[i-1] == B[j-1],则ans[i][j] = ans[i-1][j-1] + 1; 即在原有的基础后缀基础上加上延伸一个。
否则,后缀不存在,重新计算后缀,ans[i][j] = 0;
class Solution {
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param A int整型vector
* @param B int整型vector
* @return int整型
*/
int longestCommonSubarry(vector<int>& A, vector<int>& B) {
// write code here
if(A.size() == 0 or B.size() == 0)
return 0;
int res = 0;
vector<vector<int>> ans(A.size()+1,vector<int>(B.size()+1,0));
for(int i =1;i<=A.size();++i){
for(int j =1;j<=B.size();++j){
if(A[i-1] == B[j-1])
ans[i][j] = ans[i-1][j-1] + 1; //可以优化
else{
ans[i][j] = 0;
}
res = max(res, ans[i][j]);
}
}
return res;
}
};
这里可以通过使用一维数组滑动更新,实现空间优化。每次都要利用第j-1个信息,因此要先更新j在更新j-1。
每次更新的时候通过扫描前一个字符与当前字符是否相等,来考虑当前是否能够通过前一个最长序列来延续,以此省掉第一个维度。
class Solution {
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param A int整型vector
* @param B int整型vector
* @return int整型
*/
int longestCommonSubarry(vector<int>& A, vector<int>& B) {
// write code here
if(A.size() == 0 or B.size() == 0)
return 0;
int res = 0;
vector<int> ans(B.size()+1,0);
for(int i = 1; i<=A.size(); ++i){
for(int j = B.size(); j>=0; --j){
if(A[i-1] == B[j-1])
ans[j] = ans[j-1] + 1;
else{
ans[j] = 0;
}
res = max(res, ans[j]);
}
}
return res;
}
};
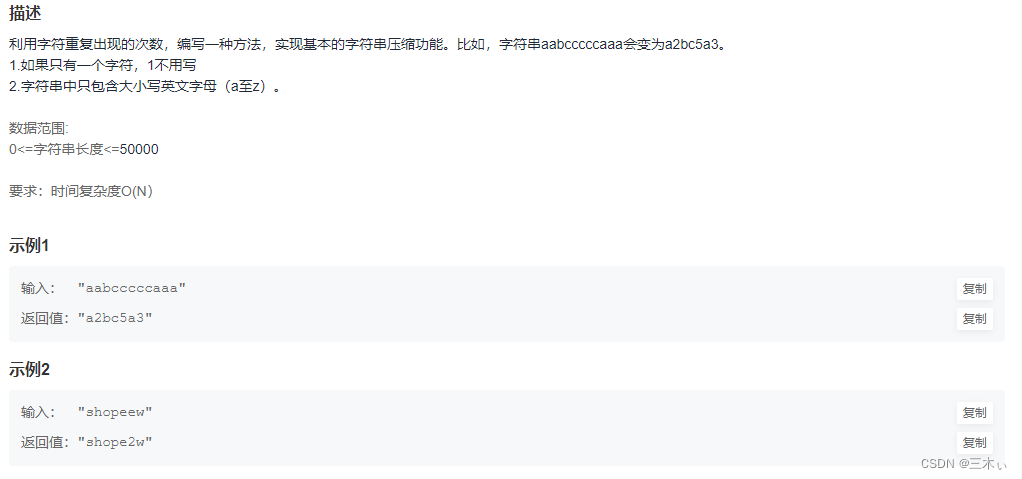
压缩字符串(一)
牛客链接:NC101 压缩字符串(一)
解法1:栈
从头到尾遍历,出现不同的元素,统计栈内元素个数,为1则不需要输出,同时清空栈,用于计算下一个元素。
class Solution {
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param param string字符串
* @return string字符串
*/
string compressString(string param) {
// write code here
stack<char> s;
string ans = "";
if(param.size() == 0)
return ans;
for(int i =0; i<param.size();++i){
if(s.size()==0 or param[i] == s.top())
s.push(param[i]);
else{
ans+=s.top();
if(s.size()>1)
ans+=to_string(s.size());
while(s.size()>0)
s.pop();
s.push(param[i]);
}
}
ans+=s.top();
if(s.size()>1)
ans+=to_string(s.size());
return ans;
}
};
