递归解决迷宫问题
1、递归的基本知识
1.1 递归的概念
方法自己调用自己,每次调用时传入不同的变量,递归有助于解决复杂的问题,同时可以让代码变得简洁。
1.2 递归的应用场景
(1) 各种数学问题:八皇后问题、汉诺塔、阶乘、迷宫问题、球和篮子问题;
(2) 各种算法中也会使用到递归,比如:快排、归并排序、二分查找、分治算法等;
(3) 用栈解决的问题。
1.3 递归需要遵守的重要规则
(1) 执行一个方法时,就创建一个新的受保护的独立空间(栈空间);
(2) 方法的局部变量是独立的,不会相互影响, 比如n变量;
(3) 如果方法中使用的是引用类型变量(比如数组),就会共享该引用类型的数据;
(4) 递归必须向退出递归的条件逼近,否则就是无限递归,出现StackOverflowError;
(5) 当一个方法执行完毕,或者遇到return,就会返回,遵守谁调用,就将结果返回给谁,同时当方法执行完毕或者返回时,该方法也就执行完毕。
2、递归解决迷宫问题
2.1 代码编写
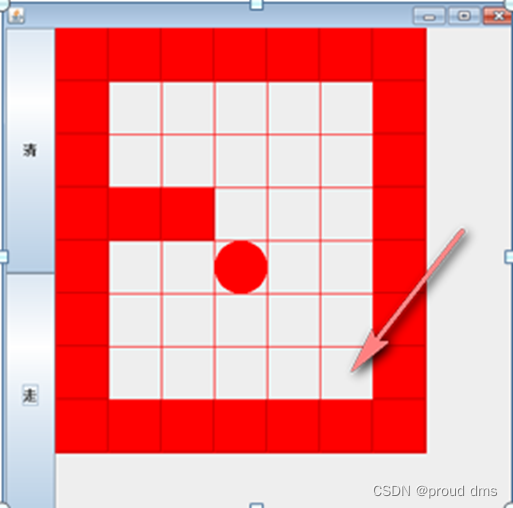
(1)创建一个二维数组,模拟迷宫,使用1表示墙
//创建一个二维数组,模拟迷宫,使用1表示墙
int[][] map = new int[8][7];
//上下全部置为1
for (int j = 0; j < 7; j++) {
map[0][j] = 1;
map[7][j] = 1;
}
//左右全部置为1
for (int i = 0; i < 8; i++) {
map[i][0] = 1;
map[i][6] = 1;
}
//中间两个挡板
map[3][1] = 1;
map[3][2] = 1;
//输出迷宫地图
for (int i = 0; i < 8; i++) {
for(int j = 0; j < 7; j++) {
System.out.print(map[i][j]+" ");
}
System.out.println();
}
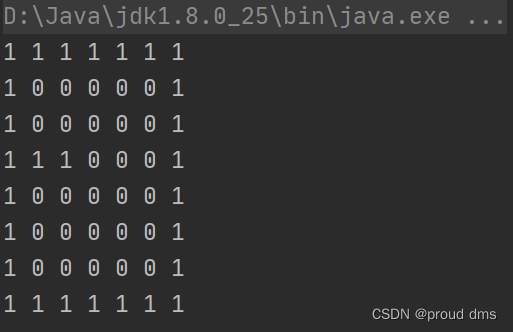
(2)使用递归回溯来给小球找路
① map表示地图,(i,j)表示从地图出发的起点位置,
② map[i][j]=0表示该点没有走过;map[i][j]=1表示为墙6;map[i][j]=2表示通路可以走;map[i][j]=3表示该点已经走过,但是走不通;
③ 确定一个策略:下-》右-》上-》左,如果该点走不通,再回溯。
//使用递归回溯来给小球找路,map表示地图,(i,j)表示从地图出发的起点位置,
//map[i][j]=0表示该点没有走过;map[i][j]=1表示为墙6;map[i][j]=2表示通路可以走;map[i][j]=3表示该点已经走过,但是走不通;
//确定一个策略:下-》右-》上-》左,如果该点走不通,再回溯。
public static boolean setWay(int[][] map, int i, int j) {
if (map[6][5] == 2) {//道路已经找到
return true;
}else {
if (map[i][j] == 0) {//如果当前这个点还没有走过
//假定该点是可以走通
map[i][j] = 2;
if (setWay(map, i + 1, j)) {//向下走
return true;
} else if (setWay(map, i, j + 1)) {//向右走
return true;
} else if (setWay(map, i - 1, j)) {//向上走
return true;
} else if (setWay(map, i, j - 1)) {//向左走
return true;
}
else {
//说明该点走不通,是死路
map[i][j] = 3;
return false;
}
}
else{
//如果map[i][j] != 0,可能是1,2,3
return false;
}
}
}
(3)编写主函数,给小球找路,并输出小球走过后标识的地图
//使用递归回溯给小球找路
setWay(map,1,1);
//输出新的地图,即小球走过的路
System.out.println("====输出小球走过后标识的地图====");
for (int i = 0; i < 8; i++) {
for(int j = 0; j < 7; j++) {
System.out.print(map[i][j]+" ");
}
System.out.println();
}
2.2 运行结果

3、最短路径
(1)策略:下-》右-》上-》左——9步
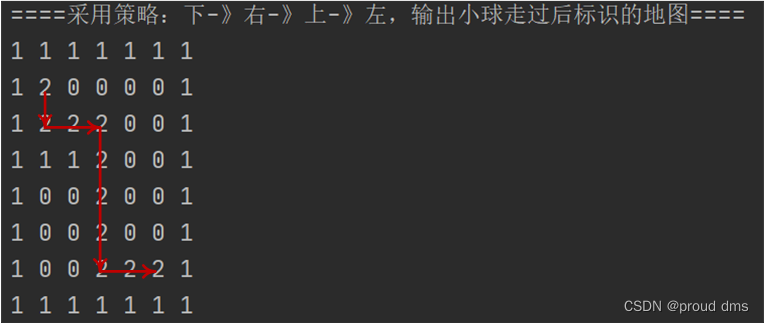
(2)策略:右-》上-》左-》下——9步
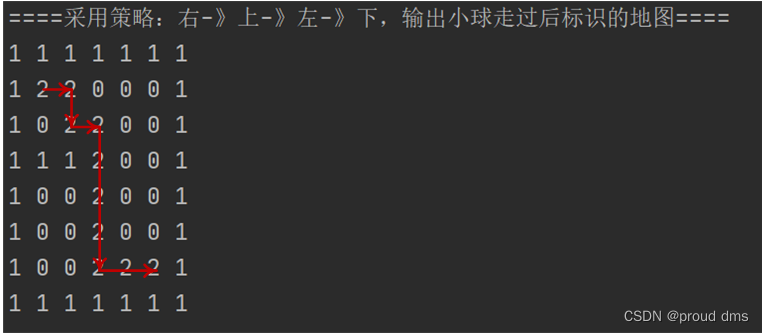
(3)策略:上-》左-》下-》右——12步
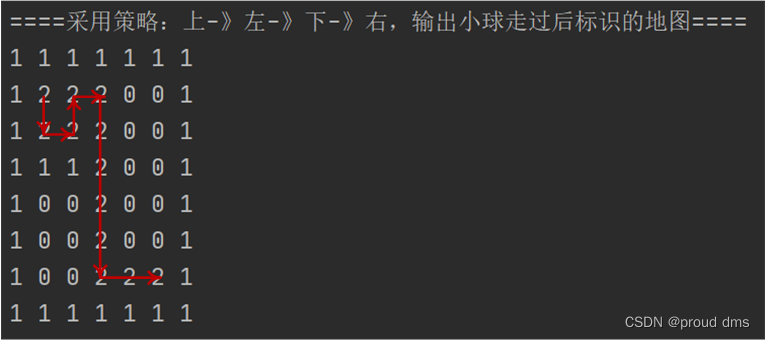
(4)策略:左-》下-》右-》上——12步
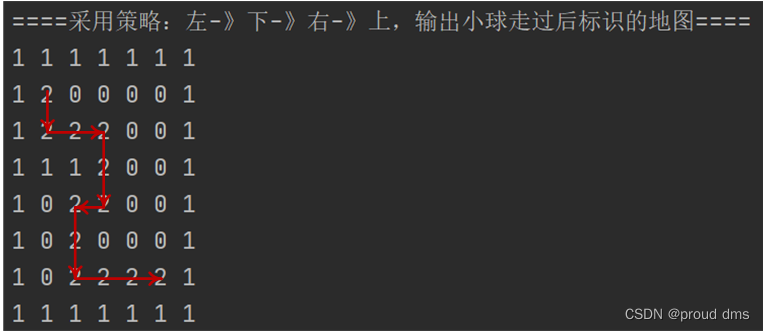
综上,采用策略:下-》右-》上-》左和策略:右-》上-》左-》下,小球走过的路径最短,最短路径步数为9步。
4、 完整代码
public class Migong {
public static void main(String[] args) {
//创建一个二维数组,模拟迷宫,使用1表示墙
int[][] map = new int[8][7];
//上下全部置为1
for (int j = 0; j < 7; j++) {
map[0][j] = 1;
map[7][j] = 1;
}
//左右全部置为1
for (int i = 0; i < 8; i++) {
map[i][0] = 1;
map[i][6] = 1;
}
//中间两个挡板
map[3][1] = 1;
map[3][2] = 1;
//输出迷宫地图
System.out.println("====输出迷宫地图====");
for (int i = 0; i < 8; i++) {
for(int j = 0; j < 7; j++) {
System.out.print(map[i][j]+" ");
}
System.out.println();
}
//输出新的地图,即小球走过的路
/*System.out.println("====采用策略:下-》右-》上-》左,输出小球走过后标识的地图====");
//使用递归回溯给小球找路
setWay(map,1,1);
for (int i = 0; i < 8; i++) {
for(int j = 0; j < 7; j++) {
System.out.print(map[i][j]+" ");
}
System.out.println();
}*/
/*System.out.println("====采用策略:右-》上-》左-》下,输出小球走过后标识的地图====");
setWay2(map,1,1);
for (int i = 0; i < 8; i++) {
for(int j = 0; j < 7; j++) {
System.out.print(map[i][j]+" ");
}
System.out.println();
}*/
System.out.println("====采用策略:上-》左-》下-》右,输出小球走过后标识的地图====");
setWay3(map,1,1);
for (int i = 0; i < 8; i++) {
for(int j = 0; j < 7; j++) {
System.out.print(map[i][j]+" ");
}
System.out.println();
}
/* System.out.println("====采用策略:左-》下-》右-》上,输出小球走过后标识的地图====");
setWay4(map,1,1);
for (int i = 0; i < 8; i++) {
for(int j = 0; j < 7; j++) {
System.out.print(map[i][j]+" ");
}
System.out.println();
}*/
}
//使用递归回溯来给小球找路,map表示地图,(i,j)表示从地图出发的起点位置,
//map[i][j]=0表示该点没有走过;map[i][j]=1表示为墙6;map[i][j]=2表示通路可以走;map[i][j]=3表示该点已经走过,但是走不通;
//确定一个策略:下-》右-》上-》左,如果该点走不通,再回溯。
public static boolean setWay(int[][] map, int i, int j) {
if (map[6][5] == 2) {//道路已经找到
return true;
}else {
if (map[i][j] == 0) {//如果当前这个点还没有走过
//假定该点是可以走通
map[i][j] = 2;
if (setWay(map, i + 1, j)) {//向下走
return true;
} else if (setWay(map, i, j + 1)) {//向右走
return true;
} else if (setWay(map, i - 1, j)) {//向上走
return true;
} else if (setWay(map, i, j - 1)) {//向左走
return true;
}
else {
//说明该点走不通,是死路
map[i][j] = 3;
return false;
}
}
else{
//如果map[i][j] != 0,可能是1,2,3
return false;
}
}
}
//使用递归回溯来给小球找路,map表示地图,(i,j)表示从地图出发的起点位置,
//map[i][j]=0表示该点没有走过;map[i][j]=1表示为墙6;map[i][j]=2表示通路可以走;map[i][j]=3表示该点已经走过,但是走不通;
//确定一个策略:右-》上-》左-》下,如果该点走不通,再回溯。
public static boolean setWay2(int[][] map, int i, int j) {
if (map[6][5] == 2) {//道路已经找到
return true;
}else {
if (map[i][j] == 0) {//如果当前这个点还没有走过
//假定该点是可以走通
map[i][j] = 2;
if (setWay(map, i , j+1)) {//向右走
return true;
} else if (setWay2(map, i-1, j )) {//向上走
return true;
} else if (setWay2(map, i, j-1)) {//向左走
return true;
} else if (setWay2(map, i+1, j )) {//向下走
return true;
}
else {
//说明该点走不通,是死路
map[i][j] = 3;
return false;
}
}
else{
//如果map[i][j] != 0,可能是1,2,3
return false;
}
}
}
//使用递归回溯来给小球找路,map表示地图,(i,j)表示从地图出发的起点位置,
//map[i][j]=0表示该点没有走过;map[i][j]=1表示为墙6;map[i][j]=2表示通路可以走;map[i][j]=3表示该点已经走过,但是走不通;
//确定一个策略:上-》左-》下-》右,如果该点走不通,再回溯。
public static boolean setWay3(int[][] map, int i, int j) {
if (map[6][5] == 2) {//道路已经找到
return true;
}else {
if (map[i][j] == 0) {//如果当前这个点还没有走过
//假定该点是可以走通
map[i][j] = 2;
if (setWay(map, i-1 , j)) {//向上走
return true;
} else if (setWay3(map, i, j-1 )) {//向左走
return true;
} else if (setWay3(map, i+1, j)) {//向下走
return true;
} else if (setWay3(map, i, j+1 )) {//向右走
return true;
}
else {
//说明该点走不通,是死路
map[i][j] = 3;
return false;
}
}
else{
//如果map[i][j] != 0,可能是1,2,3
return false;
}
}
}
//使用递归回溯来给小球找路,map表示地图,(i,j)表示从地图出发的起点位置,
//map[i][j]=0表示该点没有走过;map[i][j]=1表示为墙6;map[i][j]=2表示通路可以走;map[i][j]=3表示该点已经走过,但是走不通;
//确定一个策略:左-》下-》右-》上,如果该点走不通,再回溯。
public static boolean setWay4(int[][] map, int i, int j) {
if (map[6][5] == 2) {//道路已经找到
return true;
}else {
if (map[i][j] == 0) {//如果当前这个点还没有走过
//假定该点是可以走通
map[i][j] = 2;
if (setWay(map, i , j-1)) {//向左走
return true;
} else if (setWay4(map, i+1, j )) {//向下走
return true;
} else if (setWay4(map, i, j+1)) {//向右走
return true;
} else if (setWay4(map, i-1, j )) {//向上走
return true;
}
else {
//说明该点走不通,是死路
map[i][j] = 3;
return false;
}
}
else{
//如果map[i][j] != 0,可能是1,2,3
return false;
}
}
}
}
