队列
队列是一种先进先出的顺序表,只允许在表的一端进行插入,在另一端进行删除数据
队尾:队列中允许插入数据的一端
队头:删除数据的一端

队列的实现
对于队列需要进行头插和尾删,所以采用链式结构更加灵活和方便
(一)队列的创建
//创建队列
void QueueInit(Queue* pq)
{
assert(pq);
pq->head = pq->tail = NULL;
}
(二)队列的销毁
//销毁队列
void QueueDestroy(Queue* pq)
{
assert(pq);
QNode* cur = pq->head;
while (cur)
{
QNode* next = cur->next;
free(cur);
cur = next;
}
pq->head = pq->tail = NULL;
}
在遍历队列是可以创建一个cur指针来遍历,销毁节点最后记得置空
(三)队列插入数据
//插入数据
void QueuePush(Queue* pq, QDataType x)
{
assert(pq);
QNode* newnode = (QNode*)malloc(sizeof(QNode));
if (newnode == NULL)
{
printf("malloc fail\n");
exit(-1);
}
newnode->data = x;
newnode->next = NULL;
if (pq->tail==NULL)
{
pq->head = pq->tail = newnode;
}
else {
pq->tail->next = newnode;
pq->tail = newnode;
}
}
注:
1.创建新节点的时候,在创建完成之后一定要判断创建是否成功
2.在队列插入节点时,要考虑本身队列就没有节点的这一特殊情况,该情况下,将头节点和尾节点都指向新节点即可,其他情况下将新节点插入,尾节点指向新节点即可
(四)从队列中删除节点
//删除队头节点
void QueuePop(Queue* pq)
{
assert(pq);
assert(!QueueEmpty(pq));
if (pq->head->next==NULL)
{
free(pq->head);
pq->head = pq->tail = NULL;
}
else {
QNode* temp = pq->head;
pq->head = pq->head->next;
free(temp);
temp = NULL;
}
}
注:
1.在删除节点的过程中,要考虑仅剩一个节点的特殊情况,此时头节点和尾节点都指向同一个节点,此时将这个节点释放掉即可,如果单纯将这个节点按照平常节点来处理,将头节点释放掉,头节点指向空指针,此时尾节点就是指向野指针
(五)取出队头数据
//取出队头数据
QDataType QueueFront(Queue* pq)
{
assert(pq);
assert(!QueueEmpty(pq));
return pq->head->data;
}
(六)取出队尾数据
//取出队尾数据
QDataType QueueBack(Queue* pq)
{
assert(pq);
assert(!QueueEmpty(pq));
return pq->tail->data;
}
(七)判断队列是否为空
//判断队列是否为空
bool QueueEmpty(Queue* pq)
{
assert(pq);
return pq->head == NULL;
}
(八)求队列大小
//求取队列大小
int QueueSize(Queue* pq)
{
assert(pq);
assert(!QueueEmpty(pq));
QNode* cur = pq->head;
int size = 0;
while (cur)
{
cur = cur->next;
size++;
}
return size;
}
队列的应用场景
1.排队,保持绝对公平性
2.广度优先遍历
循环队列
链接: 设计循环队列
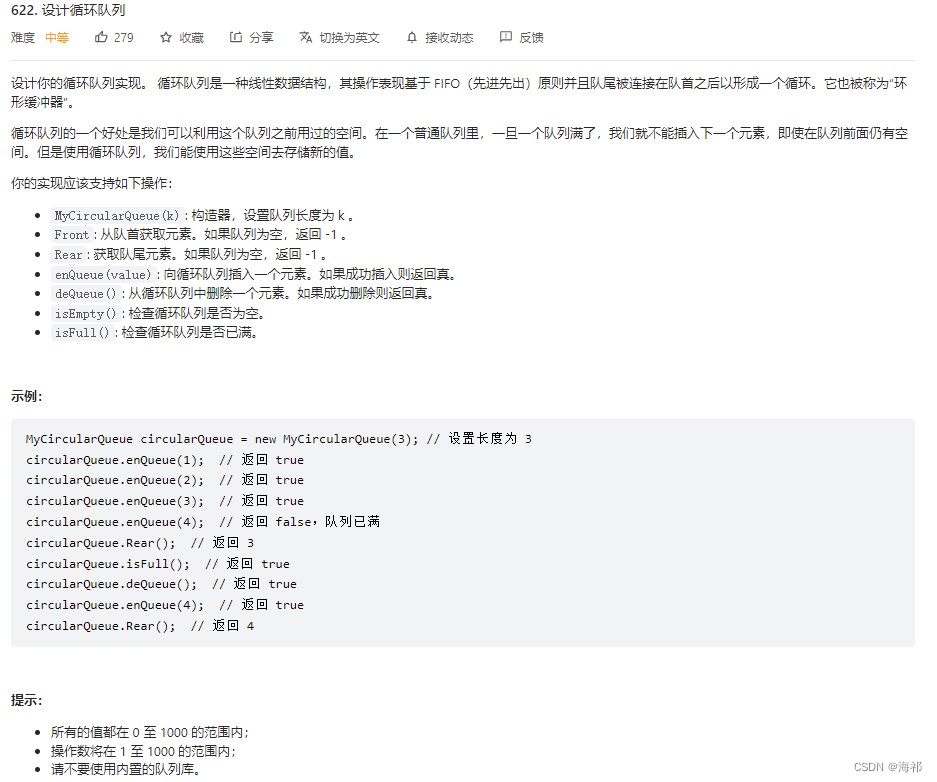
对于循环队列,就是队尾连接队首,形成一个循环
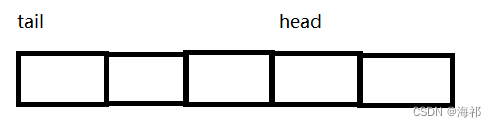
如图:
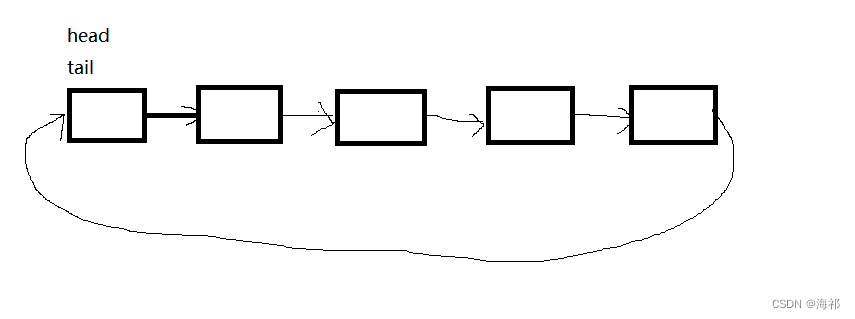
此时表示队列为空,head指向队首,tail指向队尾的下一个节点,如果插入数据,就将数据保存到节点里,将tail向后移即可,如果删除数据,将head节点向后走即可,但是这个思路中有一个问题就是:
当队列为空时:head=tail
当队列满的时候:head=tail
对于判断条件:head==tail无法区分空和满
解决方案:
(一)
可以定义一个size来记录队列数据多少来区分满和空,当size=0时,队列为空,当size=队列大小时,队列满了
(二)
多开一个空间不存储数据,如上一个队列,一共五个空间,但是只存储四个数据
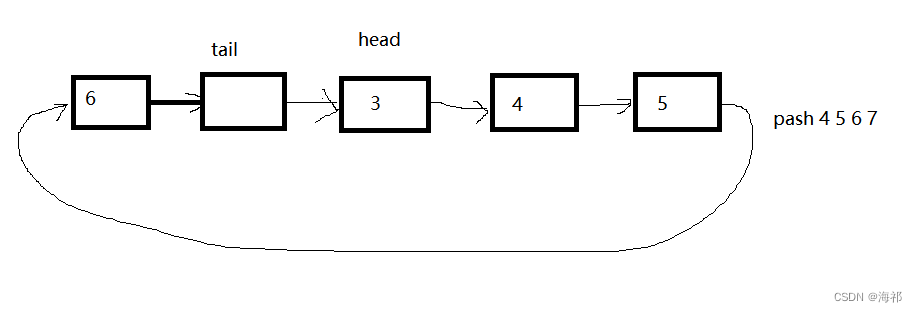
如图在队列中继续插入4,5,6,7,依次向后插入,但是插入6之后表示该队列无法再继续插入数据,判断该队列满的条件就是tail->next是否等于head
判断队列空:tail是否等于head
当然循环队列也可以用数组来实现,这时head和tail就不是指针,而是对应数组的下标,其原理和链式队列是一样的,这里不再详细画图描述,本次代码用数组来实现
typedef struct {
int* a;
int k;
int head;
int tail;
} MyCircularQueue;
MyCircularQueue* myCircularQueueCreate(int k) {
MyCircularQueue* obj=(MyCircularQueue*)malloc(sizeof(MyCircularQueue));
obj->a=(int*)malloc((k+1)*sizeof(int));
obj->head=obj->tail=0;
obj->k=k;
return obj;
}
bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
return obj->head==obj->tail;
}
bool myCircularQueueIsFull(MyCircularQueue* obj) {
int next=obj->tail+1;
if(next==obj->k+1)
{
next=0;
}
return next==obj->head;
}
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
if(myCircularQueueIsFull(obj))
{
return false;
}
obj->a[obj->tail]=value;
obj->tail++;
if(obj->tail==obj->k+1)
{
obj->tail=0;
}
return true;
}
bool myCircularQueueDeQueue(MyCircularQueue* obj) {
if(myCircularQueueIsEmpty(obj))
{
return false;
}
++obj->head;
if(obj->head==obj->k+1)
{
obj->head=0;
}
return true;
}
int myCircularQueueFront(MyCircularQueue* obj) {
if(myCircularQueueIsEmpty(obj))
{
return -1;
}
return obj->a[obj->head];
}
int myCircularQueueRear(MyCircularQueue* obj) {
if(myCircularQueueIsEmpty(obj))
{
return -1;
}
int prev=obj->tail-1;
if(obj->tail==0)
{
prev=obj->k;
}
return obj->a[prev];
}
void myCircularQueueFree(MyCircularQueue* obj) {
free(obj->a);
obj->a=NULL;
obj->head=obj->tail=0;
free(obj);
obj=NULL;
}
在这个循环队列的实现过程中,最需要注意的是在临界位置的判断与调整,如在插入数据时,如果tail再插入数据以后已经为k+1,此时tail所指使的下表标已经超出了数组的范围,因此这里要将tail置为0,而在这里更要注意插入和置0的先后顺序,我第一次写的时候将判断和置0放在前面,插入放在后面,是跑不过的,因为tail指向的是最后一个数据的下一个单元。
另外一个需要注意的是,在进行许多操作的时候,需要先进行判空,而在插入数据的时候需要先进行判断队列是否已经满了。
对于循环队列来说,不仅仅可以根据判断最后的临界值来决定改变tail或者head的值,还可以根据取模的方法,其他的我不再赘述,只看以下一道比较有代表性的题目:

在循环队列当中,如果算长度,一般情况下首先想到的就是rear-front,也就是下列的情况:
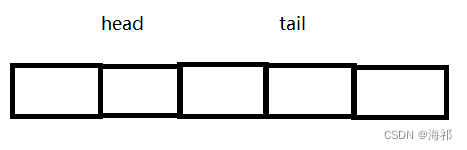
也就是tail在head之后的情况,这时rear-head没有错误
但是可能存在以下的情况:
这样的话tail-head就会产生负数,因此我们的处理方式是rear+N-head,对于第一种情况也不影响,之后再模N来取下表,可以省去判断并且重置的步骤》
