题目1

62. 不同路径【中等】

题解

动态规划

明白是二维动态规划之后就好做了

状态转移方程：dp[i][j]=dp[i][j-1]+dp[i-1][j];

class Solution {
    public int uniquePaths(int m, int n) {
        //dp初始化
        int dp[][]=new int[m][n];
        for(int i=0;i<m;i++)
            dp[i][0]=1;
        for(int j=1;j<n;j++)
            dp[0][j]=1;
        //计算
        for(int i=1;i<m;i++){
            for(int j=1;j<n;j++){
                dp[i][j]=dp[i][j-1]+dp[i-1][j];
            }
        }
        return dp[m-1][n-1];
    }
}

时间复杂度： $O (m n)$

空间复杂度： $O (m n)$ ，注意到dp[i][j]仅与第 i 行和第 i-1 行的状态有关，因此我们可以使用滚动数组代替代码中的二维数组，使空间复杂度降低为 O(n)。

组合数学

用组合数学的方法也能做，向下走有 $m ? 1$ 次，向右走有 $n ? 1$ 次，所以一共 $m + n ? 2$ 次移动，我们要从这 $m + n ? 2$ 次移动中选择 $m ? 1$ 个向下移动，所以公式为
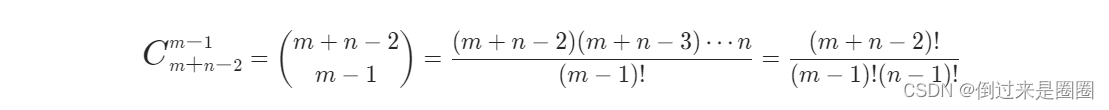
在这里插入图片描述

class Solution {
    public int uniquePaths(int m, int n) {
        long res=1;//注意结果类型是long
        for(int i=0;i<m-1;i++){
            res=res*(n+i)/(i+1);
        }
        return (int)res;
    }
}

时间复杂度： $O (m)$

空间复杂度： $O (1)$

题目2

63. 不同路径 II【中等】

题解

比上一题多了一个障碍物，有障碍物的地方到达不了dp[i][j]=0

class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int m=obstacleGrid.length,n=obstacleGrid[0].length;
        if(obstacleGrid[0][0]==1||obstacleGrid[m-1][n-1]==1)
            return 0;
        //dp初始化
        int dp[][]=new int[m][n];
        //由于第一列的位置只能从上面下来到达
        //所以如果某一个位置是障碍物,下面其余的位置也都到不了
        //直接退出循环,即剩余dp[i][0]赋0
        for(int i=0;i<m && obstacleGrid[i][0]==0;i++)
            dp[i][0]=1;
        //初始化第一行
        for(int j=1;j<n && obstacleGrid[0][j]==0;j++)
            dp[0][j]=1;
        
        //计算
        for(int i=1;i<m;i++){
            for(int j=1;j<n;j++){
                if(obstacleGrid[i][j]==1)
                    dp[i][j]=0;
                else
                    dp[i][j]=dp[i][j-1]+dp[i-1][j];
            }
        }
        return dp[m-1][n-1];
    }
}

时间复杂度： $O (m n)$

空间复杂度： $O (m n)$

优化
滚动数组优化空间复杂度

class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int m=obstacleGrid.length,n=obstacleGrid[0].length;
        //dp初始化
        int dp[]=new int[n];
        for(int j=0;j<n && obstacleGrid[0][j]==0;j++)
            dp[j]=1;
        
        //计算
        for(int i=1;i<m;i++){
            for(int j=0;j<n;j++){
                //除非有障碍物,否则dp[0]不变(延续上一行,能到还是能到,不能还是不能)
                if(obstacleGrid[i][j]==1)
                    dp[j]=0;
                //dp[j-1]是左边刚更新的值,dp[j]是上面还未更新的值
                else if(j>0)
                    dp[j]=dp[j-1]+dp[j];
            }
        }
        return dp[n-1];
    }
}