?方法:动态规划(转化为01背包)
背包问题: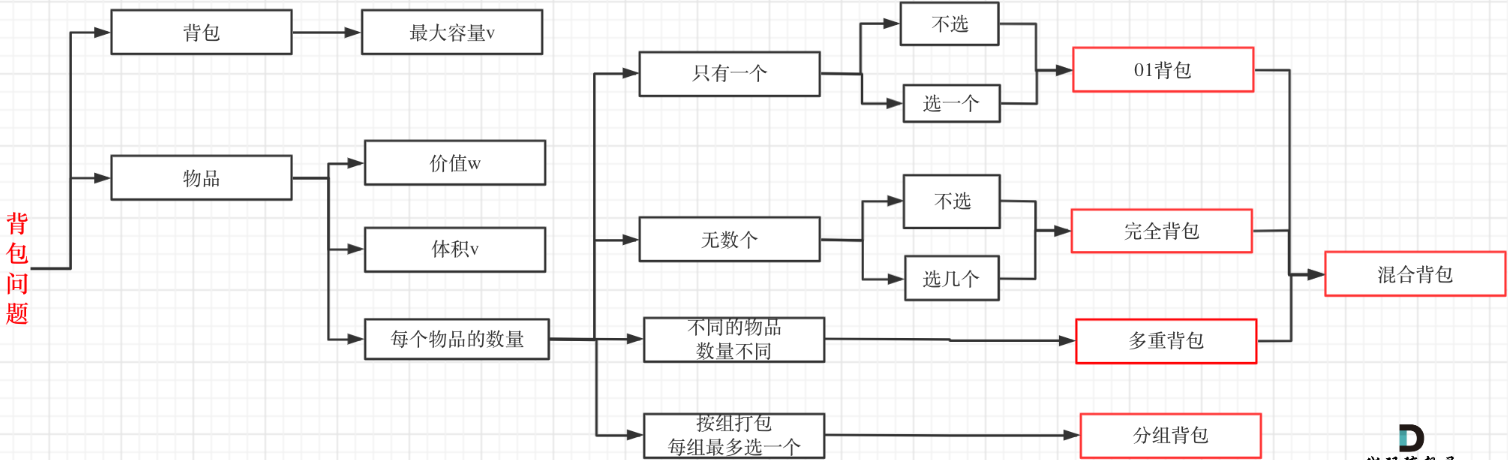
?01背包——有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i],得到的价值为value[i] 。每件物品只能用一次,求解将哪些物品装入背包,使得价值总和最大。
--二维数组
class Solution {
public boolean canPartition(int[] nums) {
int sum = 0;
for (int num : nums) {
sum += num;
}
if (sum % 2 == 1) return false;
int n = nums.length;
//背包容量
int target = sum / 2;
//dp[i][j] 的含义:有0-i个物品,容量为j的背包,所背的物品价值可以最大为dp[i][j]
int[][] dp = new int[n][target + 1];
//进行初始化
//背包容量为0时,子集元素和肯定为0,创建的二维数组初始值为0,不用显示初始化,可省略
// for (int i = 0; i < n; i++) {
// dp[i][0] = 0;
// }
//选择第一件物品,即 nums[0],当背包容量大于等于 nums[0] 时,子集元素和为 nums[0],进行初始化
for (int j = nums[0]; j <= target; j++) {
dp[0][j] = nums[0];
}
for (int i = 1; i < n; i++) {
for (int j = 1; j <= target; j++) {
//背包容量小于nums[i],无法装下
if (j < nums[i]) {
dp[i][j] = dp[i - 1][j];
} else {
//背板能装下nums[i],此时有两种选择
//不装:dp[i - 1][j],装:dp[i - 1][j - nums[i]] + nums[i],取最大值
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - nums[i]] + nums[i]);
}
}
}
return dp[n - 1][target] == target;
}
}上述代码的空间复杂度是 O(n×target)。但是可以发现在计算dp的过程中,每一行的dp值都只与上一行的dp值有关,因此只需要一个一维数组即可将空间复杂度降到 O(target)。此时的转移方程为:dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i])。
需要注意的是第二层的循环我们需要从大到小计算,因为如果我们从小到大更新dp值,那么在计算dp[j]值的时候,dp[j?nums[i]] 已经是被更新过的状态,不再是上一行的dp值。
--一维数组
class Solution {
public boolean canPartition(int[] nums) {
int sum = 0;
for (int num : nums) {
sum += num;
}
if (sum % 2 == 1) return false;
int target = sum / 2;
//题目中说每个数组中的元素不会超过100,数组的大小不会超过200
//总和不会大于20000,背包最大只需要其中一半,所以10001大小就可以了
int[] dp = new int[10001];
for (int i = 0; i < nums.length; i++) {
//每个元素一定是不可重复放入,所以从大到小遍历
for (int j = target; j >= nums[i]; j--) {
dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i]);
}
}
//集合中的元素正好可以凑成总和target
return dp[target] == target;
}
}