一道很简单的题,二叉树的前序遍历,这道题一般三种解法:
1.递归
2.迭代
3.Morris迭代算法
这篇文章主要对后两者进行记录。
一、递归法
递归法基本上是所有人的首选,代码实现也比较简单,在这里从略,直接给出代码:
class Solution {
void preorder(TreeNode* root, vector<int>& Result)
{
if(!root)
return;
Result.push_back(root->val);
if(root->left)
preorder(root->left, Result);
if(root->right)
preorder(root->right, Result);
}
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int> Result;
if(!root)
return Result;
preorder(root, Result);
return Result;
}
};
因为递归算法的参数传递比较麻烦,在这里专门写了一个函数preorder,使用引用传参的方式来及时地记录遍历的结果。
二、迭代法
递归的本质还是调用系统栈来完成的,这个过程完全可以使用栈来模拟,从而写出迭代的写法,这种写法相对递归来说细节更多一些。
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root)
{
vector<int> Result;
if(!root)
return Result;
stack<TreeNode*> S; // keep the nodes
TreeNode* Present = root;
while(!S.empty() || Present) // watch out the judgement
{
while(Present)
{
Result.emplace_back(Present->val);
S.emplace(Present);
Present = Present->left;
}
Present = S.top(); // access the top element
S.pop();
Present = Present->right;
}
return Result;
}
};
这段代码需要注意的是循环的条件,也就是:
while(!S.empty() || Present)
三、Morris迭代算法
这个算法是比较高效的,它的基本思路有些类似于数据结构课程上讲授过的线索二叉树,也就是利用二叉树中空闲的空指针指向当前节点应该遍历的下一个节点,这样做可以将栈结构完全消去,空间复杂度也可以降到常数级。
首先给出LeetCode官方题解上对Morris迭代算法的大体描述,注意其中画框的部分,它告诉我们在何时访问节点。
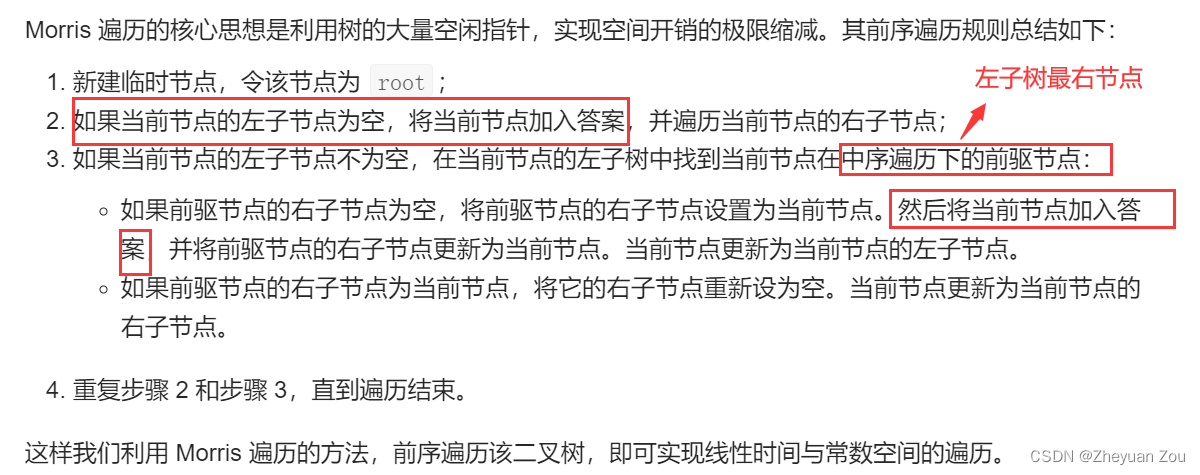
首先给出Morris迭代的代码:
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
/*Morris traversal*/
vector<int> Result;
if(!root)
return Result;
TreeNode* Current = root;
TreeNode* Morris = nullptr;
while(Current)
{
Morris = Current->left;
if(Morris) // left child is not null
{
// get the right-most children of left subtree
while(Morris->right && Morris->right != Current)
Morris = Morris->right;
// the right-most child is null
// indicating it has never been visited before
if(!(Morris->right))
{
Morris->right = Current;
// visit the node
Result.emplace_back(Current->val);
Current = Current->left;
continue; // ATTENTION THE CONTINUE
}
else
// restore the pointer to null
Morris->right = nullptr;
}
else
// left child is null, visit the node
Result.emplace_back(Current->val);
// goto the next position
Current = Current->right;
}
return Result;
}
};
代码中的Morris是为了致敬算法的提出者,它本质的含义是当前节点左子树的最右侧的节点。在先序遍历中,实际访问节点的时机有两个:
1.左子树为空
2.左子树最右节点的指针为空时(保证根先序)
关于Morris算法更加直观的理解,这里推荐一篇博客,这篇文章将Morris算法的先中后序遍历都做了比较详细的解释,配图便于理解。
小小的树遍历,其实可做的文章一点都不少。
