dfs剪枝 P1120 小木棍

题目：
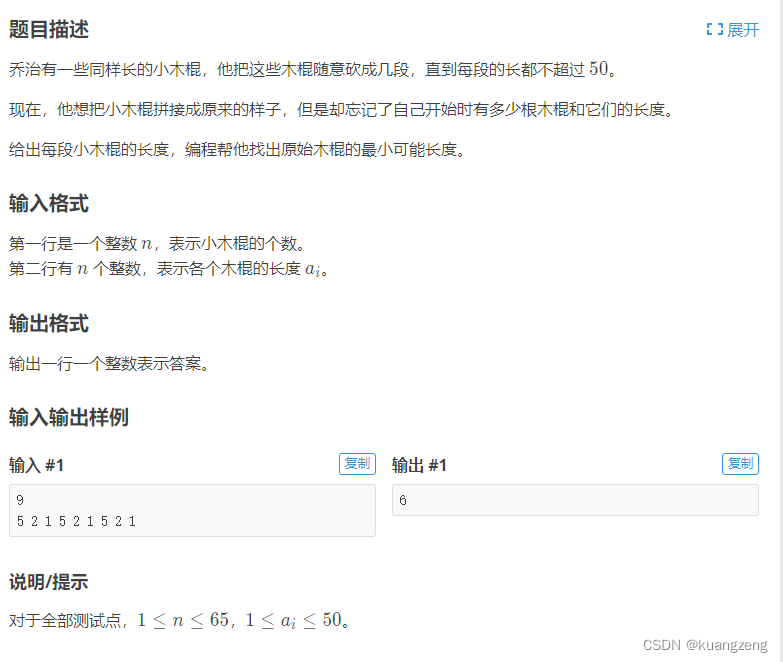
链接https://www.luogu.com.cn/problem/P1120
在这里插入图片描述
思路：用dfs进行可以组成多少长度的大木棍进行全遍历，数据量是1-65，所以全遍历会超时，所以需要进行剪枝，
剪枝1，小木棍组成的长度大于我们需要组成的大木棍的长度的话就不进行下去了，
剪枝2，组成的大木棍一定是大于小木棍的最大值，
剪枝3，组成多少长度的大木棍一定是小木棍总长度的倍数，
剪枝4，把木棍排序，优先从大的小木棍开始拿可以跟快的合成大木棍，
剪枝5，如果小木棍拼不成，那么和这个小木棍长度相等的小木棍都拼不成
剪枝6，如果组成的小木棍等于需要组成的木棍的长度或者等于0，但是后面拼不了了返回到上一层
剪枝7，找到方案直接退出，因为是从最小组成的长度开始的所以可以直接退出
优化：函数前面加上 inline 会稍微快一点

代码：

#include <bits/stdc++.h>
using namespace std;
int n,m;
int a[100005],b[1005];
int maxs=0,maxsnum=0;
//       
inline void dfs(int s,int i,int sum,int g) { // s:组成的小木棍长度  i:当前所在的数组位置
								// sum：需要组成的大木棍的长度  g：当前还剩余的根数
	if(s==sum) {
        dfs(0,0,sum,g-1);
        return ;
    }
    if(g==0){
       printf("%d",sum);
	   exit(0);//剪枝7，找到方案直接退出
    }
    int l=0; //l用于记录上一个小木棍的值
    for(int j=i;j<n;j++){
    	if(b[j]==0&&a[j]+s<=sum&&l!=a[j]){ //剪枝1，小木棍组成的长度大于我们需要组成的大木棍的长度的话就不进行下去了， 剪枝5，如果小木棍拼不成，那么和这个小木棍长度相等的小木棍都拼不成
    		b[j]=1;
    		dfs(s+a[j],j,sum,g);
    		l=a[j];//记录上一个小木棍的值
    		b[j]=0;
    		if(s==0||s+a[j]==sum) return;/*剪枝6，如果s+a[j]等于需要组成的木棍的长度或者等于0，
    		                               但是后面拼不了了 返回到上一层*/
		}
    	
	}
}
inline bool cmp(int x,int y){// 从大到小
	return x>y;
}

int main() {
    //cin >> n;
	scanf("%d",&n);
    int maxnum=0;
    for(int i=0; i<n; i++) {
        //cin >> a[i];
        scanf("%d",&a[i]);
        maxs+=a[i];
    }
   sort(a,a+n,cmp);//剪枝4，把木棍排序，优先从大的小木棍开始拿可以跟快的合成大木棍，
    for(int i=a[0]; i<=maxs; i++) { //剪枝2，组成的大木棍一定是大于小木棍的最大值，
        if(maxs%i==0) {//剪枝3，组成多少长度的大木棍一定是小木棍总长度的倍数，
			memset(b,0,n);
            dfs(0,0,i,maxs/i);
        }
    }
    return 0;
}