[数据结构与算法] 请回答数据结构【红黑树】

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 请回答数据结构【红黑树】 -> 正文阅读

[数据结构与算法]请回答数据结构【红黑树】

BingWallpaper27

0.Intro

红黑树是一种自平衡二叉搜索树。每个节点存储一个表示“颜色”（“红色”或“黑色”）的额外位，用于确保树在插入和删除期间保持平衡。当树被修改时，新树被重新排列并“重新绘制”以恢复限制树在最坏情况下可能变得多么不平衡的着色属性。这些属性被设计成可以有效地执行这种重新排列和重新着色。

From https://en.wikipedia.org/wiki/Self-balancing_binary_search_tree

1. Red-Black Tree

通过对任何一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保没有一条路径会比其他路径长出两倍，因而是接近平衡的。接近平衡其实比平衡更好一点，因为相对平衡对于计算机来说实际上差别不大（对计算机来说其实logN和2logN差别不是很大），但是严格平衡是通过不断旋转来提高效率的，基于这样的原因，红黑树效率不必AVL差，但是反而旋转更少，因此总体效率更优，因此现在使用红黑树更多一点，而不是AVL树

1.1 红黑树的性质

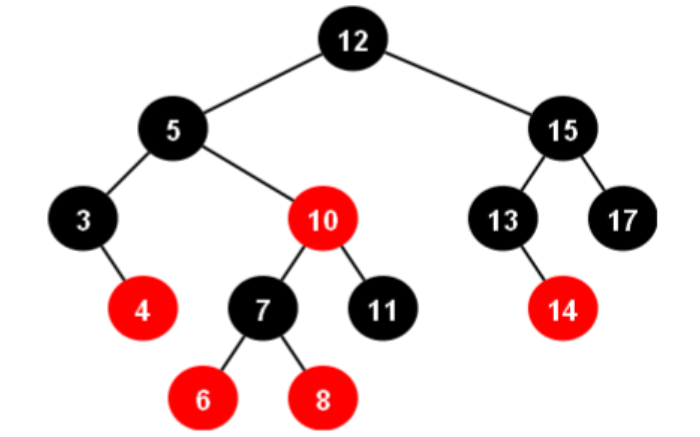
🍁 每个结点不是红色就是黑色
🍁 根节点是黑色的
🍁 如果一个节点是红色的，则它的两个孩子结点是黑色的(没有连续的红色节点)
🍁 对于每个结点，从该结点到其所有后代叶结点的简单路径上，均包含相同数目的黑色结点（每条路上包含相同数量黑色节点）

每个叶子结点都是黑色的(此处的叶子结点指的是空结点/NIL)

1.2 红黑树推论

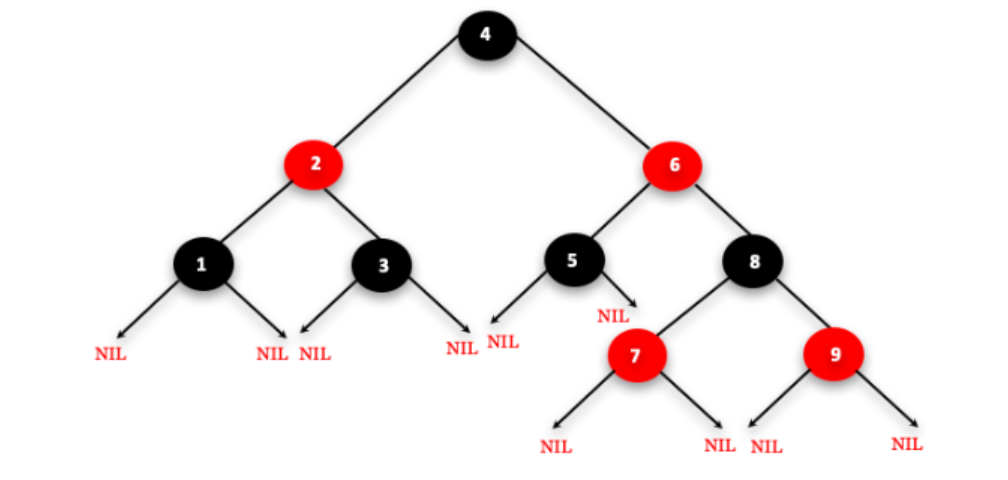
🐉 路径：
??最短路径：全部由黑色节点构成
??最长路径：一黑一红，黑色节点数量等于红色节点
🐉 假设黑色节点有N个：
??最短路径长度：logN
??最长路径长度：2logN

2. 实现红黑树

2.0 红黑树节点结构

enum Color
{
    RED,
    BLACK,
};

template<class K,class V>
struct RBTreeNode
{
    RBTreeNode<K, V>* _left;
    RBTreeNode<K, V>* _right;
    RBTreeNode<K, V>* _parent;
    pair<K, V> _kv;
    Color _col;

    RBTreeNode(const pair<K,V>&  kv)
    :_left(nullptr)
    ,_right(nullptr)
    ,_parent(nullptr)
    ,_kv(kv)
    ,_col(RED)
    {}
};

这时候我们有一个问题，为什么要将节点的默认颜色给成红色的？

黑的好还是红的好?

插入红的会破坏规则：

🍁 如果一个节点是红色的，则它的两个孩子结点是黑色的(没有连续的红色节点)

插入黑的会破坏规则：

🍁 对于每个结点，从该结点到其所有后代叶结点的简单路径上，均包含相同数目的黑色结点（每条路上包含相同数量黑色节点）

我们选择消耗低的，还是插入默认红的比较好

2.1 构造函数

	RBTree()
	:_root(nullptr)
		{}

2.2 Insert

2.2.0 处理搜索部分

搜索树部分类似于AVL和BSTree的插入逻辑

//空树
if (_root==nullptr)
{
    _root = new Node(data);
    _root->_col = BLACK;//根必须是黑的
    return make_pair(_root, true);
} 

Node* parent = nullptr;
Node* cur = _root;

//1. 找适当的空位置
while (cur)
{
    if (cur->_kv.first<data.first)
    {
        parent = cur;
        cur = cur->_right;
    }
    else if (cur->_kv.first<data.first)
    {
        parent = cur;
        cur = cur->_left;
    }
    else
    {//重复
        return make_pair(cur, false);
    }
}

//2. cur走到空 可以链接
Node* newnode = new Node(data);
newnode->_col = RED;

if (parent->_kv.first <data.first)
{
    parent->_right = newnode;
    newnode->_parent = parent;
}
else
{
    parent->_left = newnode;
    newnode->_parent = parent;
}
cur = newnode;
//处理
    
    return make_pair(kv, true);
}

关键是处理红黑节点

2.2.1 处理红黑节点

因为新节点的默认颜色是红色，因此：如果其双亲节点的颜色是黑色，没有违反红黑树任何性质，则不
需要调整；但当新插入节点的双亲节点颜色为红色时，就违反了性质三不能有连在一起的红色节点，此
时需要对红黑树分情况来讨论：

parent.color	条件	处理
BLACK	不需要调整	插入完成
RED	违反规则3	需要处理

如果parent节点是红的，那么就会出现多种情况，需要处理，情况1可以通变色处理，但是情况2+3则因为最长路径已经超过最短路径的两倍所以无法变色解决，需要旋转

下面的图中我们约定:cur为当前节点，p为父节点，g为祖父节点，u为叔叔节点

情况	cur	parent	grandparent	uncle	处理方案
情况一：叔叔存在且为红	RED	RED	BLACK	exist && RED	pu变黑，g变红，继续往上走
情况二: 叔叔不存在或为黑（直线）	RED	RED	BLACK	!exist \|\| exist && BLACK	单旋转+变色
情况三; 叔叔不存在或为黑（折线）	RED	RED	BLACK	!exist \|\| exist && BLACK	双旋转+变色

2.2.2 Situation1

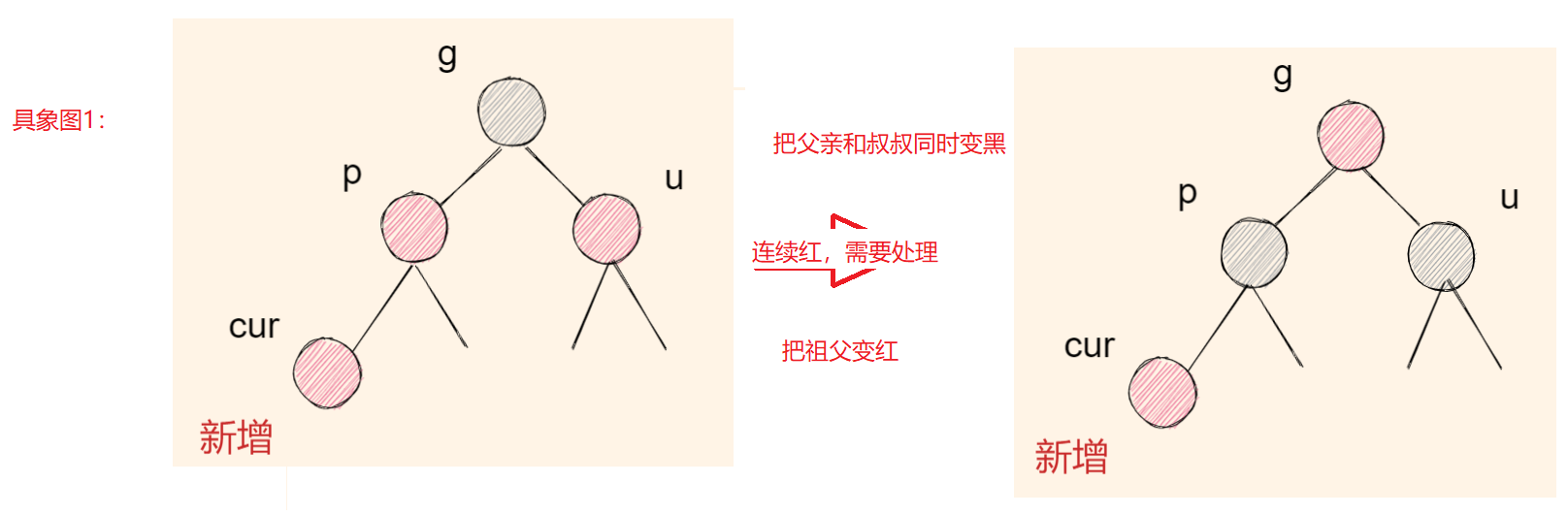
🍁 情况一: cur为红，p为红，g为黑，u存在且为红

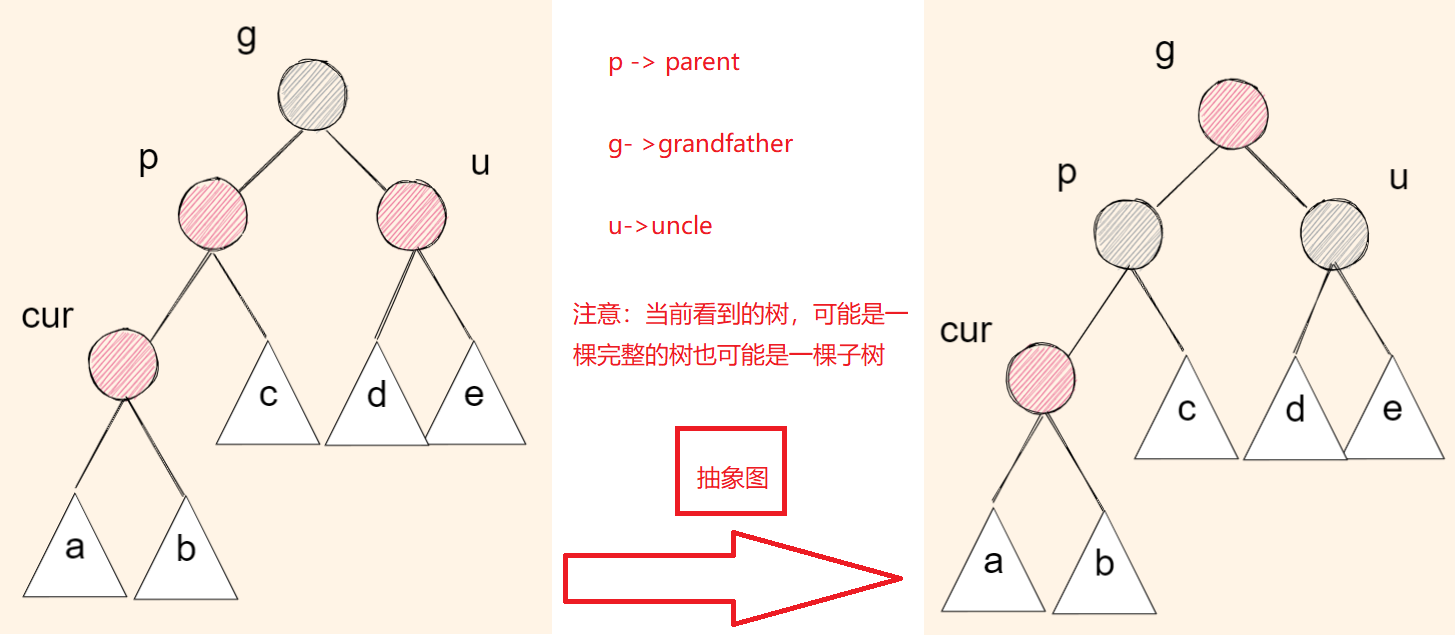
具象图	描述	操作
具象图1：	g已经到顶了	pu变黑，g变红
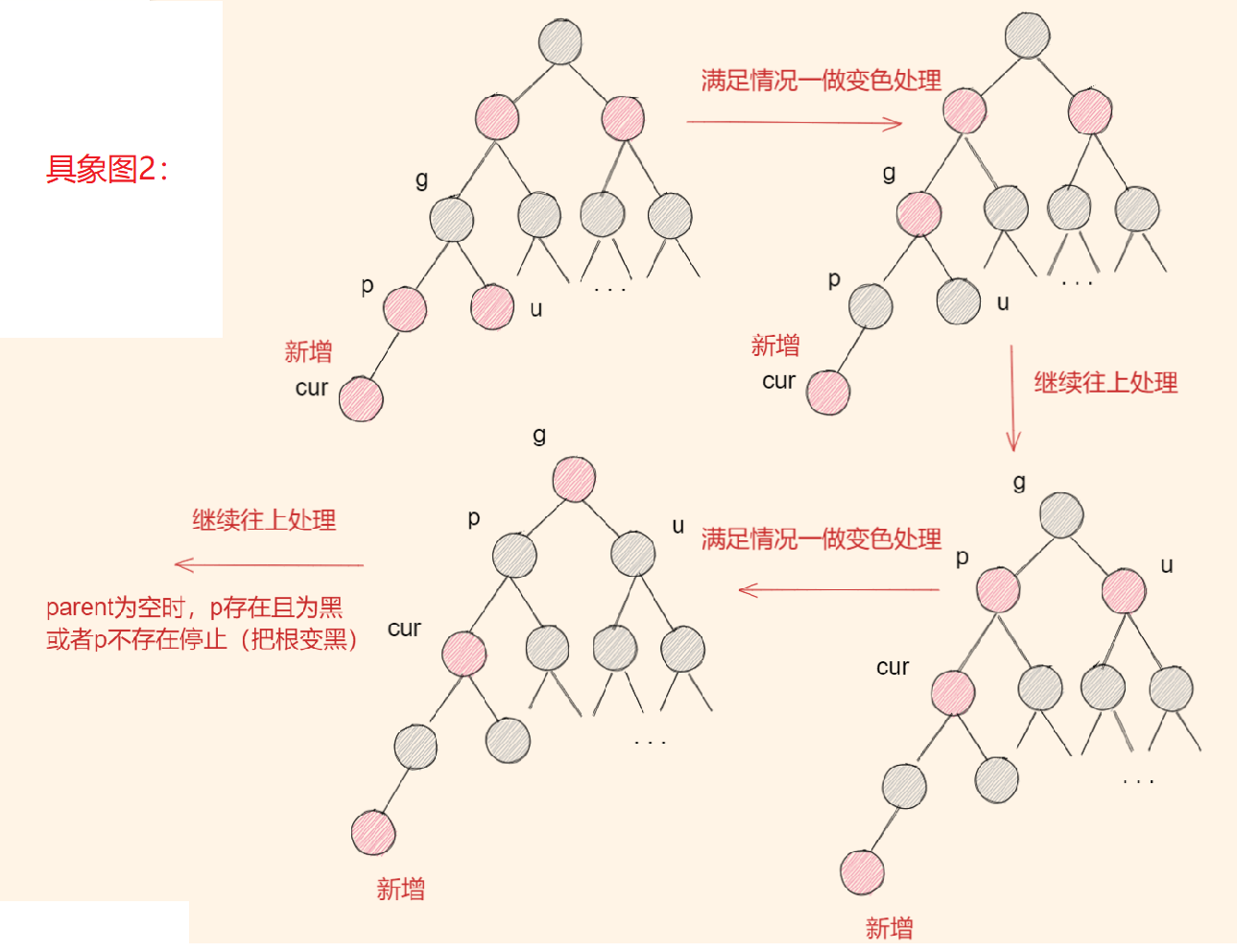
具象图2：	符合具象图1但是修改完其他节点不符合	不断执行情况1，直到parent为空时，p存在且为黑，或者p不存在停止（把根变黑）

2.2.3 Situation2

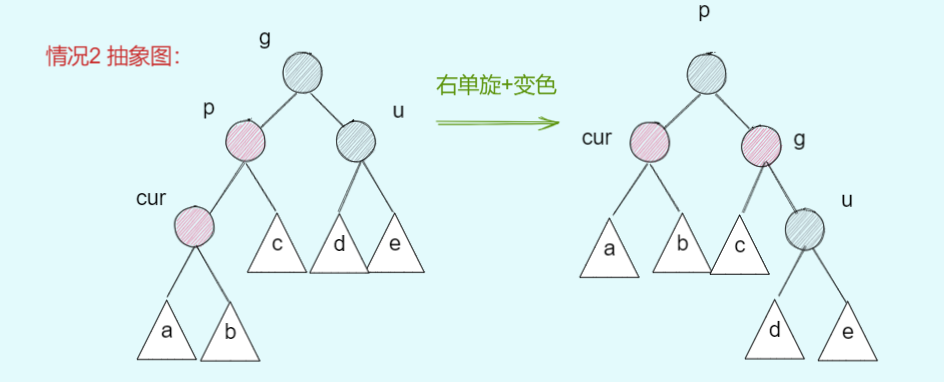
🍁 情况二: cur为红，p为红，g为黑，u不存在/u为黑
情况二中，无非是还会出现一种情况是左旋，但是说到底都是单旋转中的一种,关键在于

parent/grandparent/cur关系	旋转操作	变色操作
p为g的左孩子，cur为p的左孩子	右单旋转	p、g变色–p变黑，g变红
p为g的右孩子，cur为p的右孩子	左单旋转	p、g变色–p变黑，g变红

?? 为什么不能直接染色?

看到下图可能会有一些疑问：为什么我不能把p变黑，g变红，简单来就可以了，还要搞什么旋转呢？这是因为首先原来插入之前是一棵红黑树，那么右路如果有uncle就是需要整一条右路上要两个黑节点才能满足规则五，如果没有uncle节点就要满足至少有一个黑，所以说如果直接改变颜色，那么会导致要么右路只有一个黑节点，要么就是右路干脆没有黑节点，所以说一定要采取旋转方式，才能满足规则五

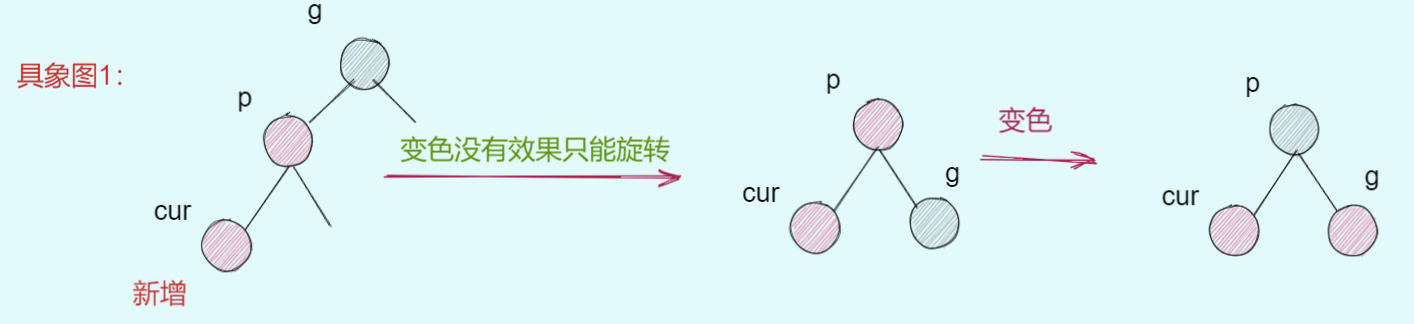
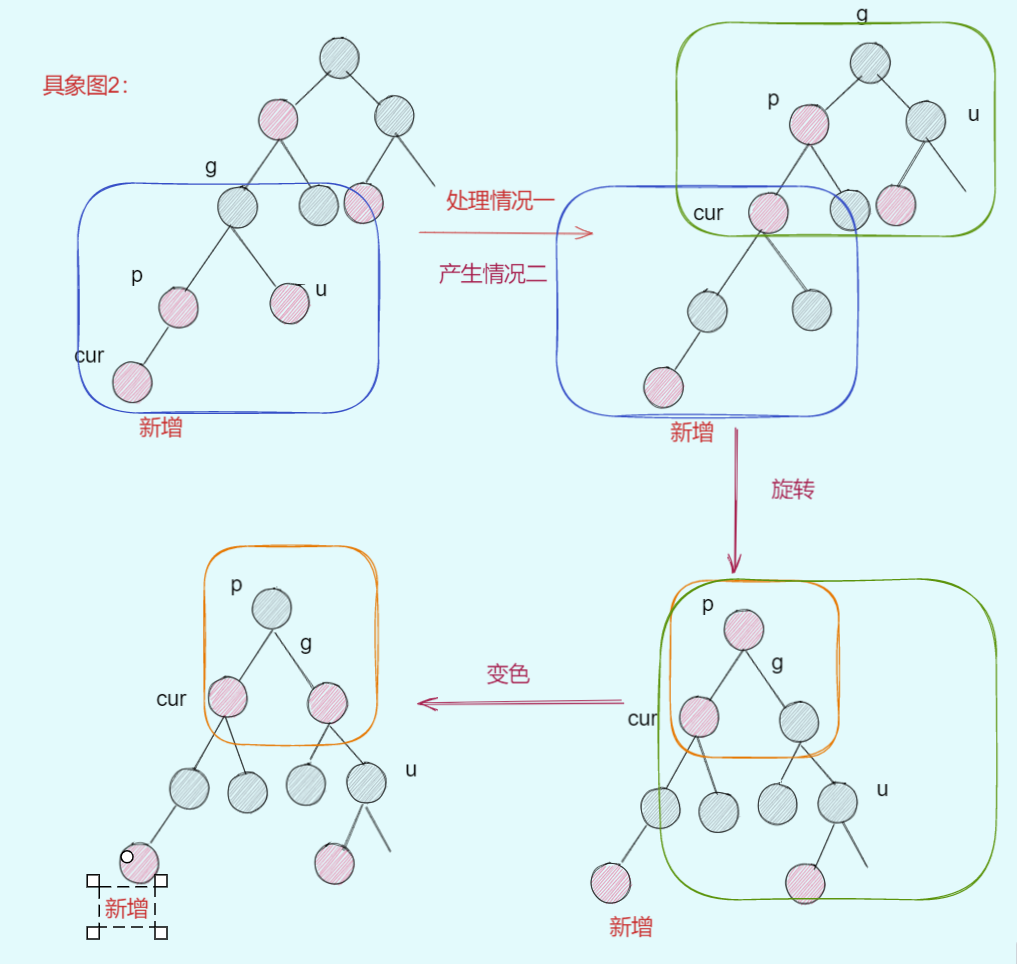
具象图（以右单旋为例）	描述	操作
具象图1：	`uncle !exist
具象图2：	符合情况一且处理之后产生情况二	处理情况一+右单旋+p变黑，g变红

2.2.4 Situation3

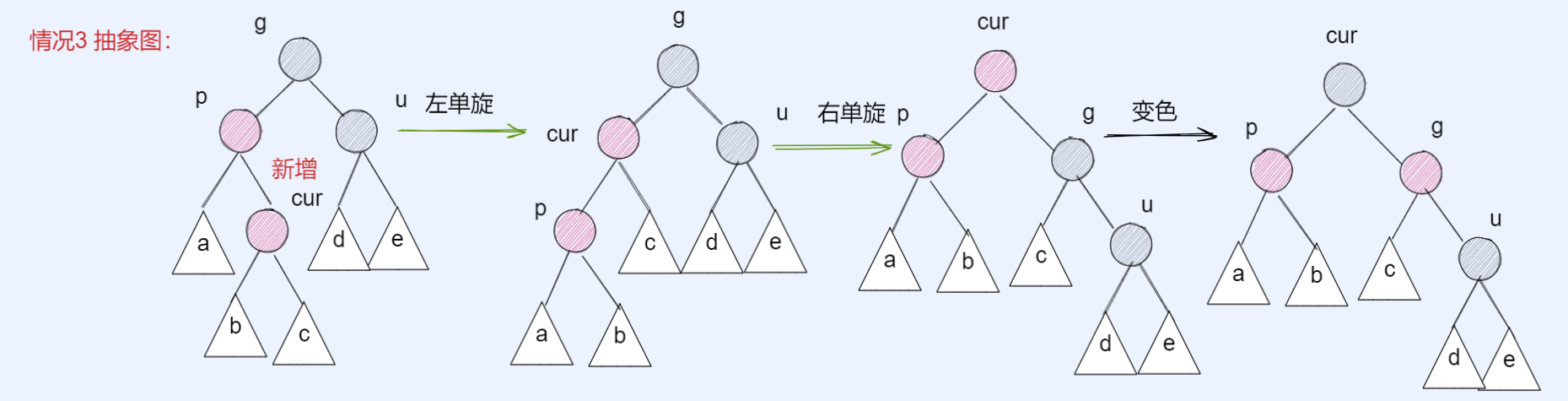
🍁 情况三: cur为红，p为红，g为黑，u不存在/u为黑

情况三看上去好像和情况二很像，其实差别在于情况三的结构，同时他是一个双旋

parent/grandparent/cur关系	旋转操作1	旋转操作2	变色操作
p为g的左孩子，cur为p的右孩子	左单旋转	右单旋转	cur、g变色–cur变黑，g变红
p为g的右孩子，cur为p的左孩子	右单旋转	左单旋转	cur、g变色–cur变黑，g变红

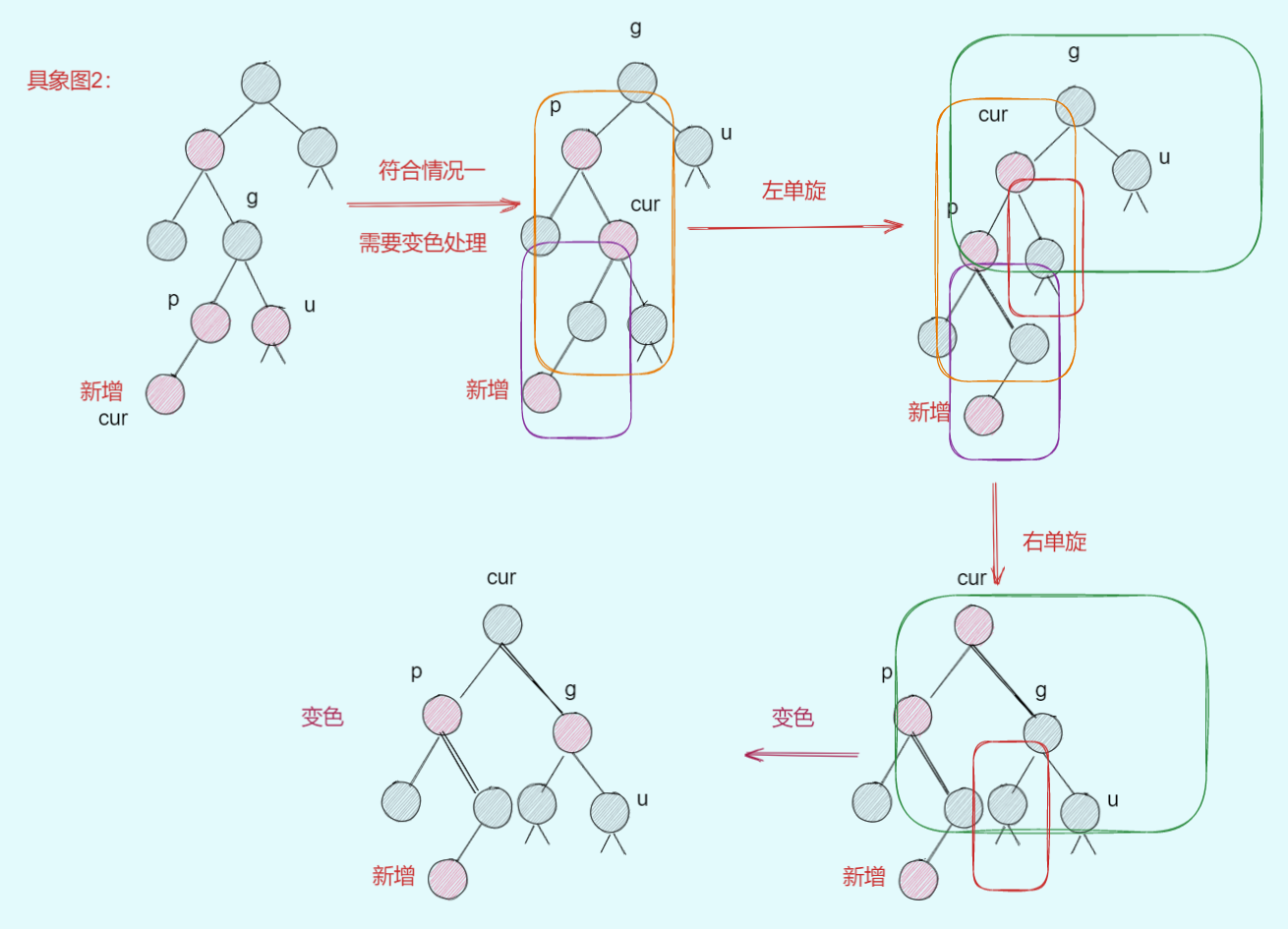
具象图（以右单旋为例）	描述	操作
具象图1：	`uncle !exist
具象图2：	符合情况一且处理之后产生情况三	处理情况一+左单旋+右单旋+cur变黑，g变红

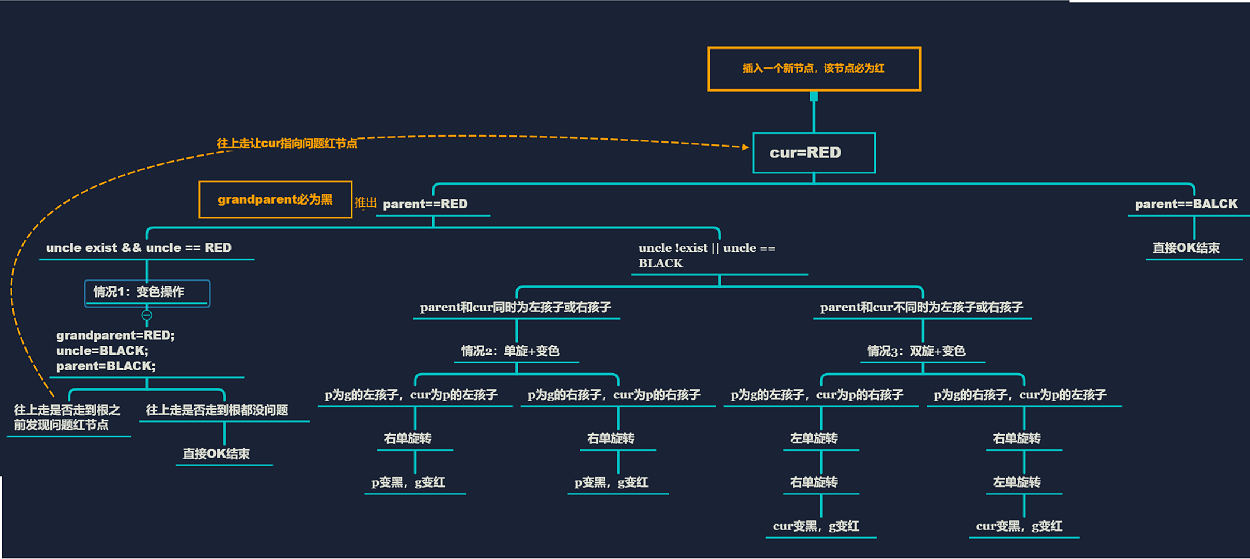
2.2.5 分类讨论总结

插入一个新节点，新节点必是红的

2.2.6 实现插入

2.2.6.1 插入本体

//插入
pair<Node*, bool> Insert(const pair<K, V>& data)
{
    //空树
    if (_root==nullptr)
    {
        _root = new Node(data);
        _root->_col = BLACK;//根必须是黑的
        return make_pair(_root, true);
    } 

    Node* parent = nullptr;
    Node* cur = _root;

    //1. 找适当的空位置
    while (cur)
    {
        if (cur->_kv.first<data.first)
        {
            parent = cur;
            cur = cur->_right;
        }
        else if (cur->_kv.first>data.first)
        {
            parent = cur;
            cur = cur->_left;
        }
        else
        {//重复
            return make_pair(cur, false);
        }
    }

    //2. cur走到空 可以链接
    Node* newnode = new Node(data);
    newnode->_col = RED;

    if (parent->_kv.first <data.first)
    {
        parent->_right = newnode;
        newnode->_parent = parent;
    }
    else
    {
        parent->_left = newnode;
        newnode->_parent = parent;
    }
    cur = newnode;

    //3.判断处理条件
    //如果父亲存在，且颜色为红色就需要处理
    while (parent && parent->_col == RED)
    {	
        //抓住叔叔是关键
        Node* grandfather = parent->_parent;
    //a. 首先父亲在祖父左边的情况
        if (parent==grandfather->_left)
        {
            Node* uncle = grandfather->_right;
            //情况1：uncle 存在且为红
            if (uncle && uncle->_col ==RED)
            {
                parent->_col = uncle->_col = BLACK;
                grandfather->_col = RED;
                //继续往上处理
                cur = grandfather;
                parent = cur->_parent;
            }

            //情况2+3 uncle不存在或者uncle存在且为黑
            else//此时变色无法处理
            {
                //情况2：单旋
                if (cur==parent->_left)
                {   //1. 右单旋
                    _Rotate_R(grandfather);
                    //2. 变色
                    grandfather->_col = RED;
                    parent->_col = BLACK;
                } 
                else//情况3：双旋
                {
                    _Rotate_L(parent);
                    _Rotate_R(grandfather);
                    cur->_col = BLACK;
                    grandfather->_col = RED;
                }
                break;//根是黑的了，不会往上影响直接break
            }
        } 

        //b. 首先父亲在祖父左边的情况
        else//parent == grandfather->_right
        {
            Node* uncle = grandfather->_left;
            //情况1：uncle 存在且为红 
            if (uncle && uncle->_col==RED)
            {
                uncle->_col=parent->_col = BLACK;
                grandfather->_col = RED;
                //继续往上递归
                cur = grandfather;
                parent = cur->_parent;//这个肯定有父亲
            } 
            //情况 2+3： uncle不存在或为黑
            else
            {
                if (parent->_right==cur)
                {
                    _Rotate_L(grandfather);
                    parent->_col = BLACK;
                    grandfather->_col = RED;
                } 
                else
                {
                    _Rotate_R(parent);
                    _Rotate_L(grandfather);
                    cur->_col = BLACK;
                    grandfather->_col = RED;
                }
                break;
            }
        }
    }
    //默认修改根节点为黑色
    _root->_col = BLACK;
    return make_pair(newnode, true);
}

2.2.6.2 旋转函数

void _Rotate_R(Node* parent)
		{
			Node* subL = parent->_left;
			Node* subLR = subL->_right;
			//1.旋转
			parent->_left = subLR;
			if (subLR)
			{
				subLR->_parent=parent;
			}
			subL->_right = parent;
			Node* grandparent = parent->_parent;//记录爷爷
			parent->_parent = subL;

			//2. 修改父子关系
			if (parent == _root)
			{//原来的父亲做了根节点
				_root = subL;
				_root->_parent = nullptr;
			}
			else
			{//修改爷爷和父亲链接
				if (grandparent->_left==parent)
					grandparent->_left = subL;
				else
					grandparent->_right = subL;
				subL->_parent = grandparent;
			}
		}

		void _Rotate_L(Node* parent)
		{
			Node* subR = parent->_right;
			Node* subRL = subR->_left;
			//1. 旋转
			parent->_right = subRL;
			if (subRL)
			{
				subRL->_parent = parent;
			}
			subR->_left = parent;
			Node* grandparent = parent->_parent;
			parent->_parent = subR;

			//2. 修改父子关系
			if (_root==parent)
			{
				_root = subR;
				_root->_parent = nullptr;
			} 
			else
			{
				if (grandparent->_left == parent)
					grandparent->_left = subR;
				else
					grandparent->_right = subR;
				subR->_parent = grandparent;
			}
		}

2.3 Erase

和AVL树类似，红黑树的删除只谈谈思想

删除节点一定是左为空或者右为空，然后让父亲链接自己的孩子
- 删除的是红色节点，直接就没有什么问题
- 删除的是黑色节点，可能导致连续的红节点，或者一条路径上少了一个黑节点
  - 后继还有红节点，变色成黑的
  - 后继没有红节点可能还要旋转

具体有很多种情况可以参照https://www.cnblogs.com/fornever/archive/2011/12/02/2270692.html

2.4 Find

和搜索树如出一辙

Node* Find(const K& key)
{
    Node* cur = _root;
    while (cur)
    {
        if (cur->_kv.first>key)
        {
            cur = cur->_left;
        }
        else if (cur->_kv.first<key)
        {
            cur = cur->_right;
        }
        else
        {
            return cur;
        }
    }
    return nullptr;
}

2.5 析构函数

void _Destroy(Node* root)
{
    if (root==nullptr)
    {
        return;
    }
    _Destroy(root->_left);
    _Destroy(root->_right);
    delete root;
}

//析构
~AVLTree()
{
    _Destroy(_root);
    _root = nullptr;
}

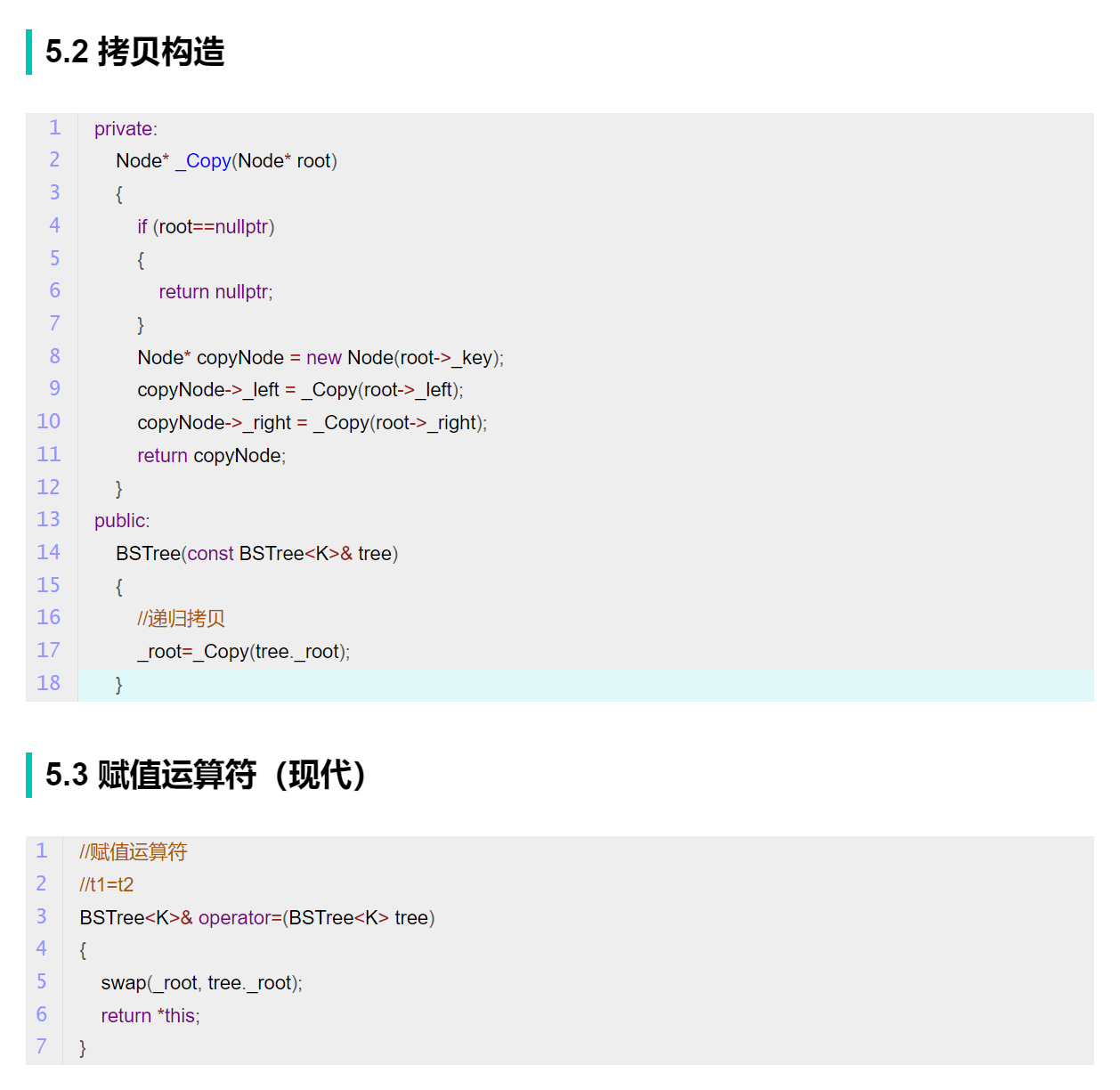
2.6 拷贝构造和赋值运算符

可以参考搜索二叉树，和之前的如出一辙

https://blog.csdn.net/Allen9012/article/details/124435568

2.7 CheckBalance

我们需要写一个树来查一下我们的插入操作正不正确，是否插入形成了一个红黑树

为了验证是否是红黑树，我们还是利用几点原则

2.7.1 黑色的根

if (_root==nullptr)
{
    return true;
}
//1.黑根
if (_root->_col==false)
{
    cout<<"root是红色"
    return false;
}

2.7.2 没有连续的红色节点

方法就是遍历，然后找到红色节点，去查找父亲是不是红色节点，如果是红色就返回false

2.7.3 每条路径上的黑色节点数量相等

前序遍历，从根节点走到每一个NIL节点，只要是黑色就count++，如果走到了NIL节点就return，然后此时上一层栈帧的++不影响其他层的count，于是可以实现

用一个vector去记录每个路径的黑色接点数量，如果最后都是相等的，那么就是说明是红黑树
不想要走完每条路线才最后比较，可不可以找一条路径作为标准，只要其他路和这条路线不相等就说明不是红黑树，可以找最左路径做黑色节点的参考值

bool _CheckBalance(Node*root,int black_num,int count)
{
    if (root ==nullptr)
    {
        if (count != black_num)
        {//3.路径黑节点数相等
            cout << "路径上黑色节点的数量不相等" << endl;
            return false;
        }
        return true;
    }

    //2.遍历红节点，查父亲是不是红的，不要查孩子因为孩子可能没有
    if (root->_col==RED && root->_parent->_col==RED)
    {
        cout << "存在连续的红色节点" << endl;
        return false;
    }

    if (root->_col==BLACK)
    {
        count++;
    }
    return _CheckBalance(root->_left,black_num,count)
                && _CheckBalance(root->_right,black_num,count);
}

bool  CheckBalance()
{
    if (_root==nullptr)
    {
        return true;
    }
    //1.黑根
    if (_root->_col==false)
    {
        cout<<"root是红色"<<endl;
        return false;
    }
    //2. 每条路径走到NIL节点，遇到黑++，找最左路径做黑色节点的参考值
    int black_num = 0;
    Node* left = _root;
    while (left)
    {
        if (left->_col==BLACK)
        {
            black_num++;
        }
        left = left->_left;
    }
    int count = 0;//count计算该条路的值
    //3. 用子函数来递归遍历
    return _CheckBalance(_root,black_num,count);
}