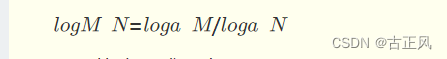B-树:绝对平衡的多叉查找树
B-树:就是B树,B-Tree,是m阶平衡搜索树(B:balance)。B树是绝对平衡的,左右子树高度差是0,不像AVL树,可以为1(这里的m阶是指最多有m个地址域)
-
AVL树:2 阶平衡搜索树,平衡因子<=1,一个结点有两个地址域,一个数据域
-
B 树:m阶平衡搜索树,平衡因子==0,一个结点有m个地址域,有m-1个数据域
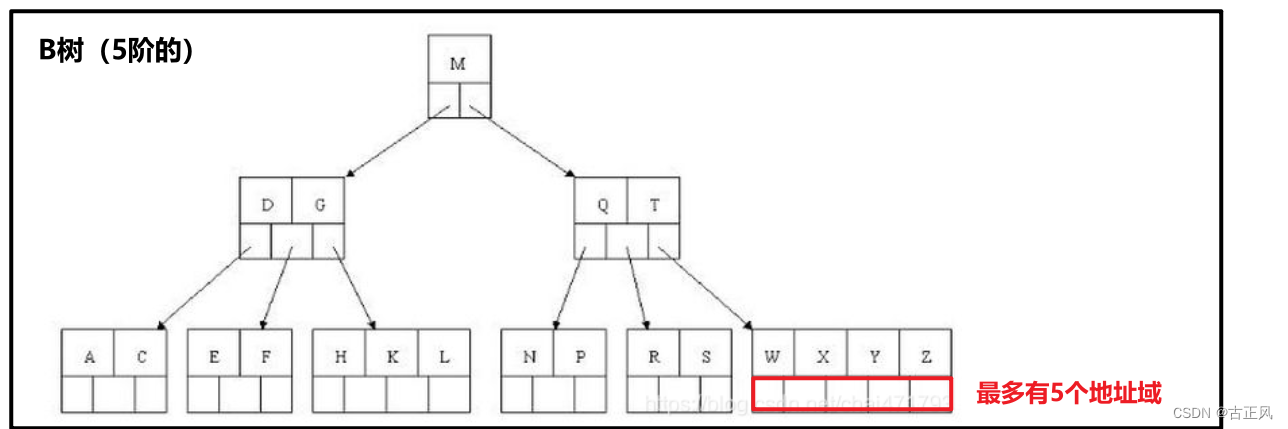
B树应用场景:文件索引系统的实现
2-3-4树可以理解为4阶的B树
B树的插入
插入规则


为什么B树除根节点和叶结点外,其他结点至少有ceil[m/2]个孩子?
答:因为其他结点是通过分裂产生的,分裂的前提是原来的结点满了到m个了,把中间的往上提,剩下的左边的成为左孩子,右边的成为右孩子,比如说5阶B树,当有5个孩子时候就要分裂,中间的提上去,左右各剩两个孩子,两孩子有 三地址域,所以其他结点至少有ceil[5/2]==3个孩子
插入示例
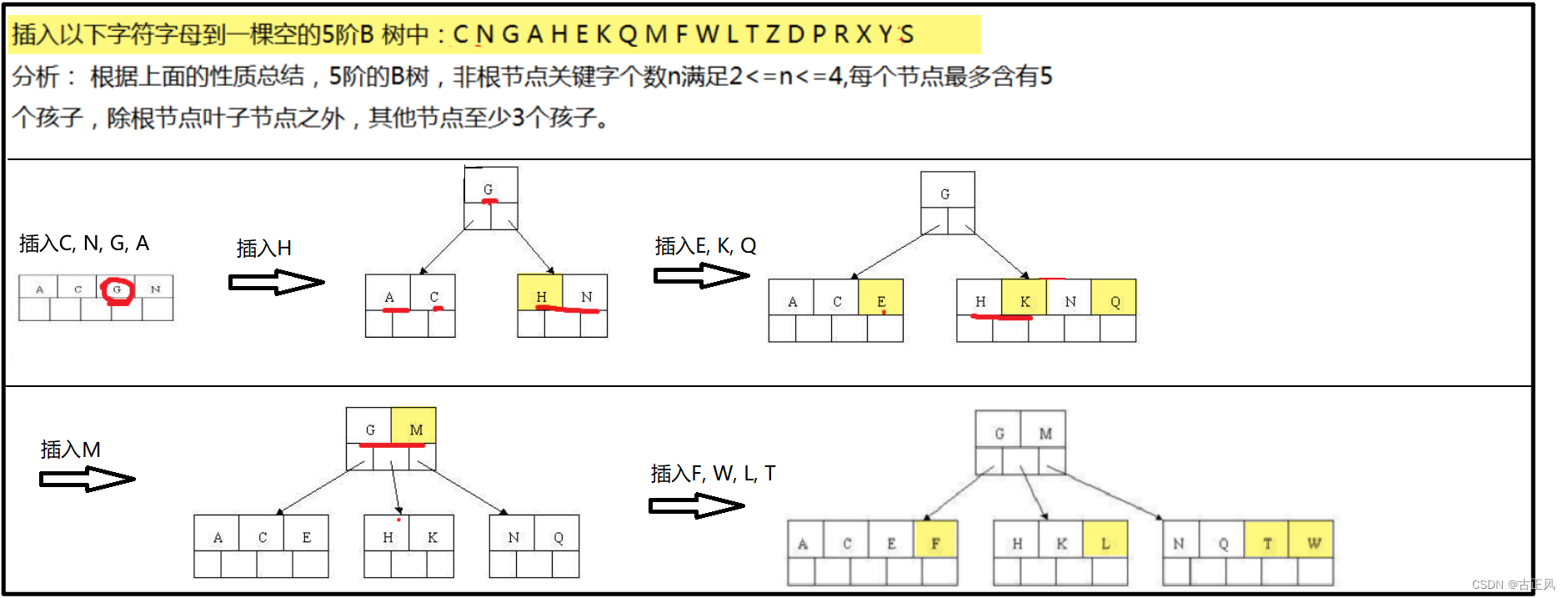
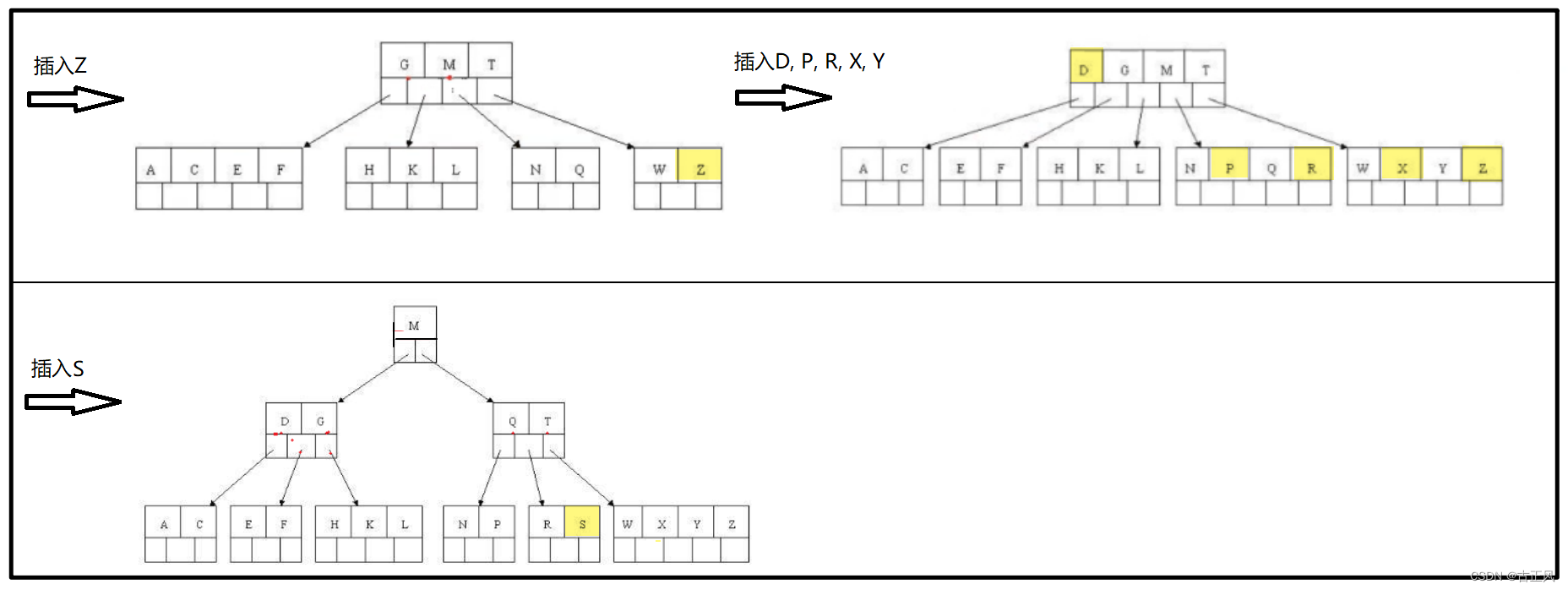
B树的删除

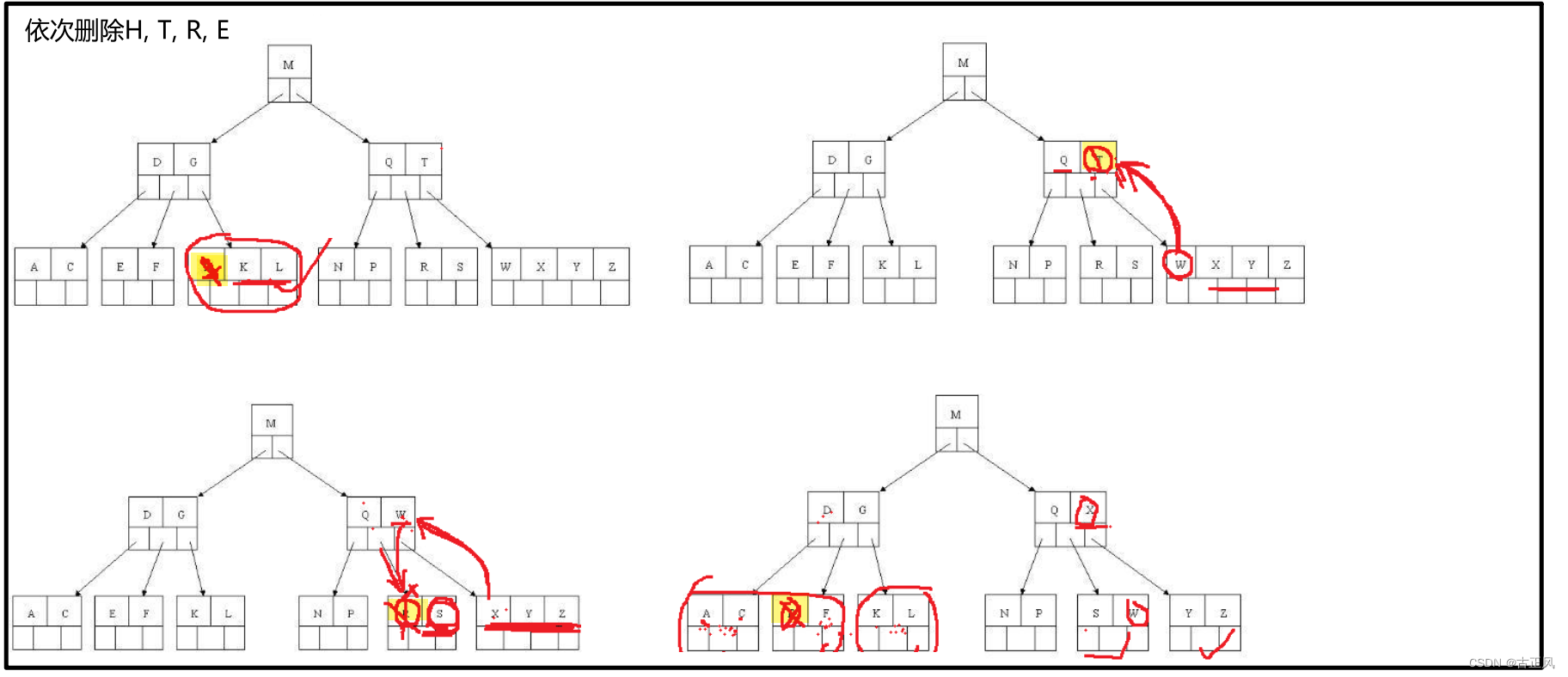
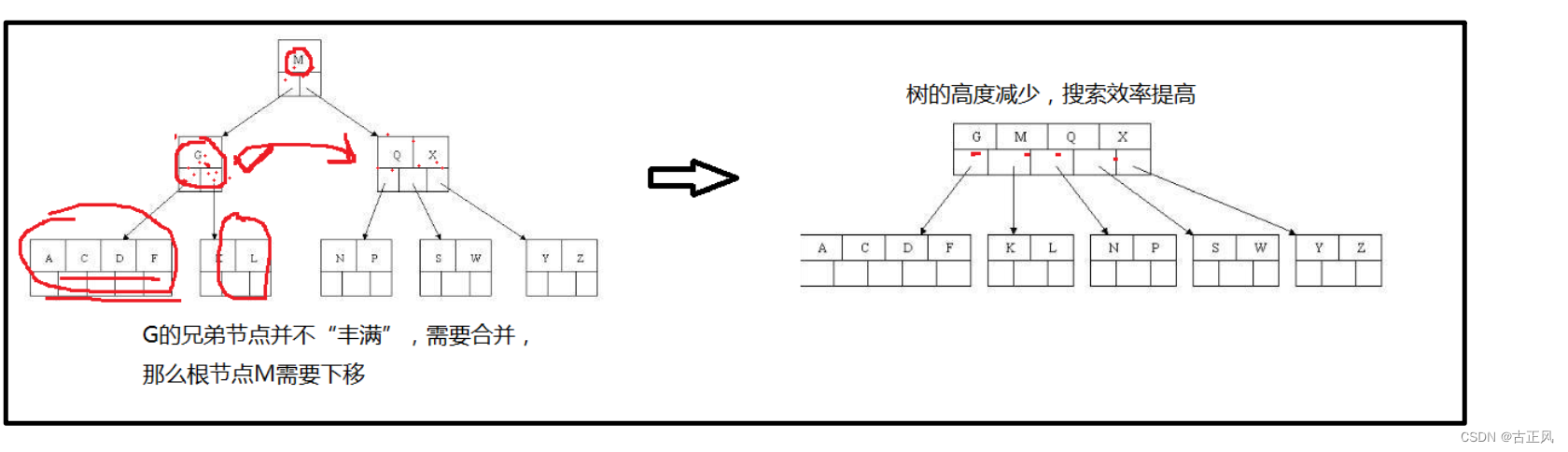
B树的磁盘IO优势和搜索效率
每一个结点包含的地址域就是磁盘每一块的大小
层数就是磁盘IO的次数
使用B树作为磁盘索引的优势:更少的磁盘IO(logmN),更快的搜索算法(二分log2N),m和2都是底数
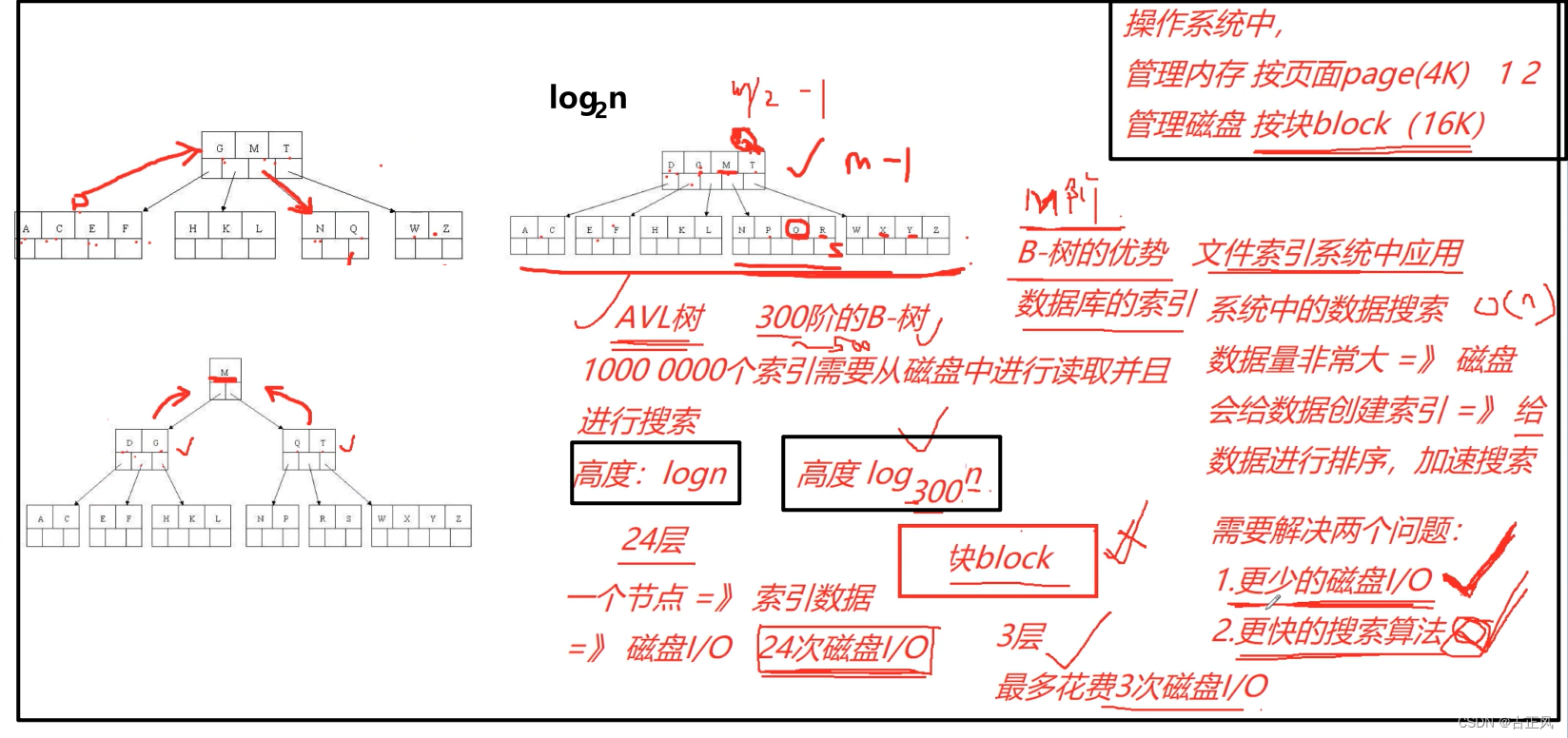
换底公式:
蓝色块代表索引项,红点代表索引项对应的数据(比如学号),黄色块是地址域
离根节点越近磁盘IO越少,读的越快
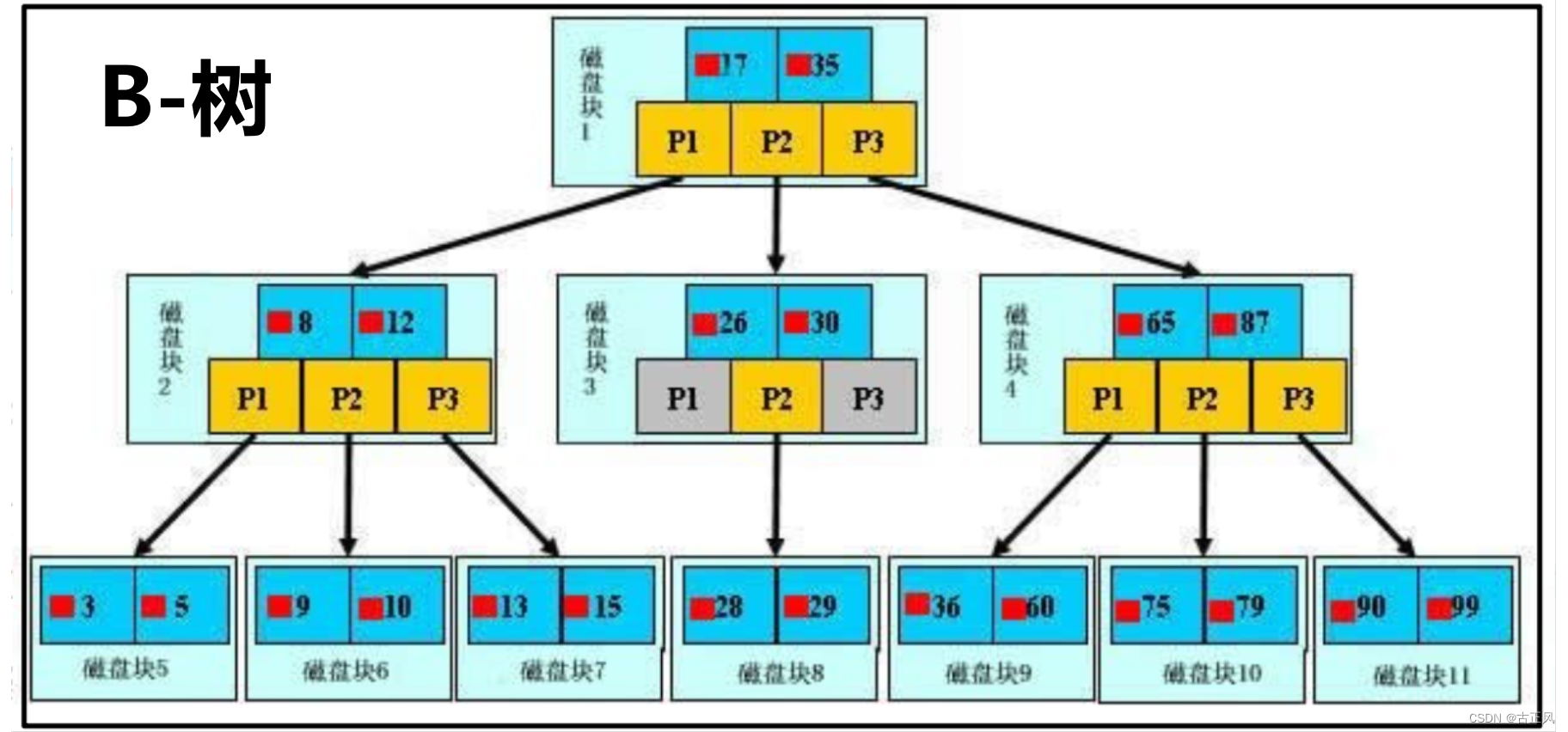
B+树:非叶子结点只存索引
B+树是B树的一种变形树,m阶的B+树和B树的区别:
-
非叶子结点只存索引项,不存数据(数据即指向具体信息的指针,那个红点)
-
叶子结点有前面的所有索引项,数据也是存在叶子结点中
-
叶子结点中关键字进行有序连接
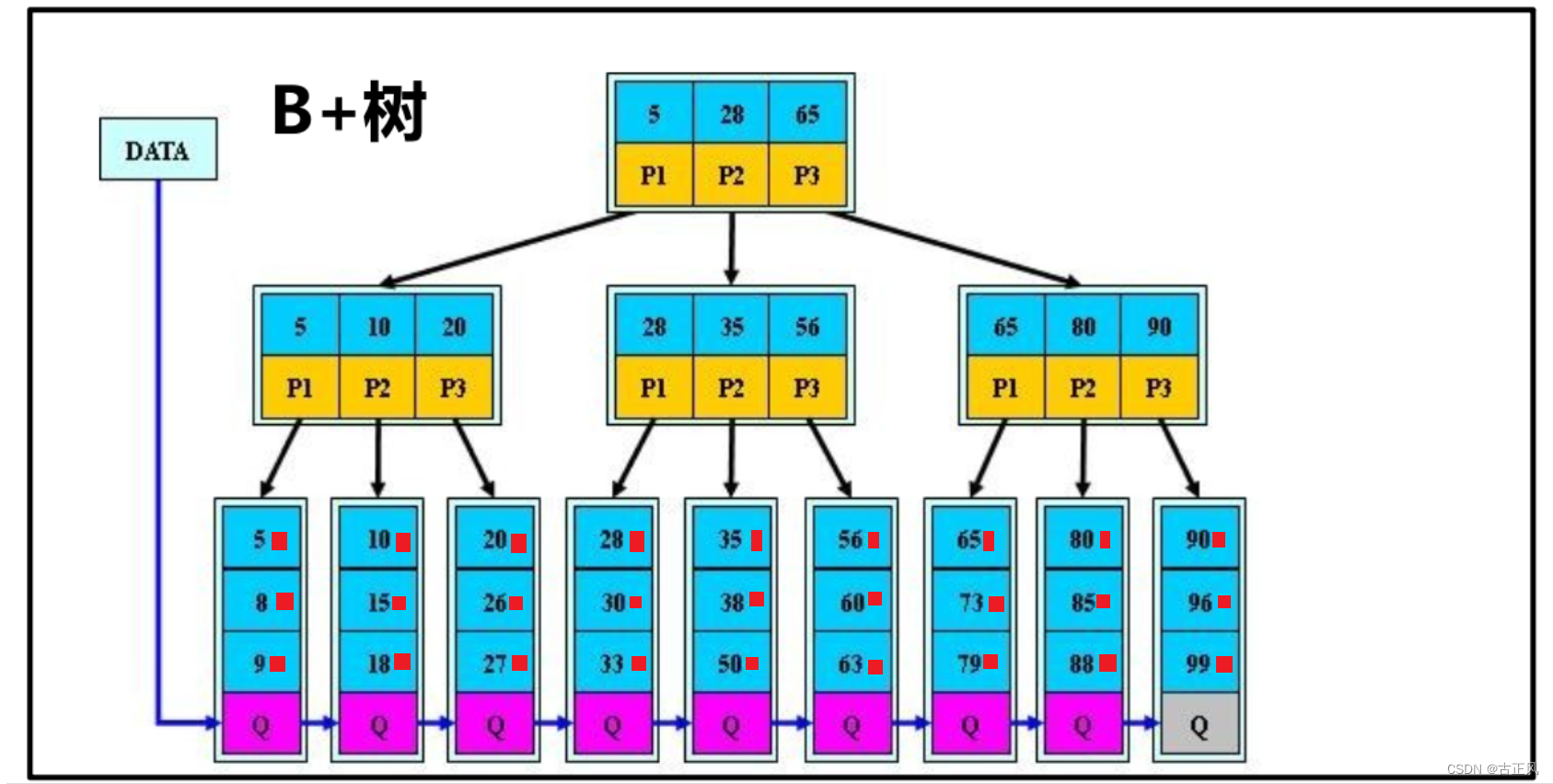
B+树所有叶子结点包含全部关键字信息,及指向含有这些关键字记录的指针,且叶子结点中关键字进行有序链接
非叶子结点相当于是叶子结点的索引,叶子结点相当于是存储(数据)的数据层
B+树作索引
MySQL数据库索引采用的是B+树

举个例子:假设磁盘中的一个盘块容纳16Bytes,而一个关键字2Bytes,一个关键字具体信息指针2Bytes。一棵9阶的B-tree(一个结点最多8个关键字)的内部结点需要2个盘块。而B+树内部结点只需要1个盘块。
当需要把内部结点读入内存中的时候,B树就比B+树多一次盘块查找时间(在磁盘中就是盘片旋转的时间)
说到底就是因为:B+树一个非终端结点只存索引项(不存具体信息指针),所以与B树同样大小的结点,B+树可以比B树存更多的索引项,所以在找某一个索引项的时候,B+树的磁盘IO更少,也就更快,并且B+树更有利于基于范围的查询
B-树和B+树区别

B*树:分支结点加兄弟指针
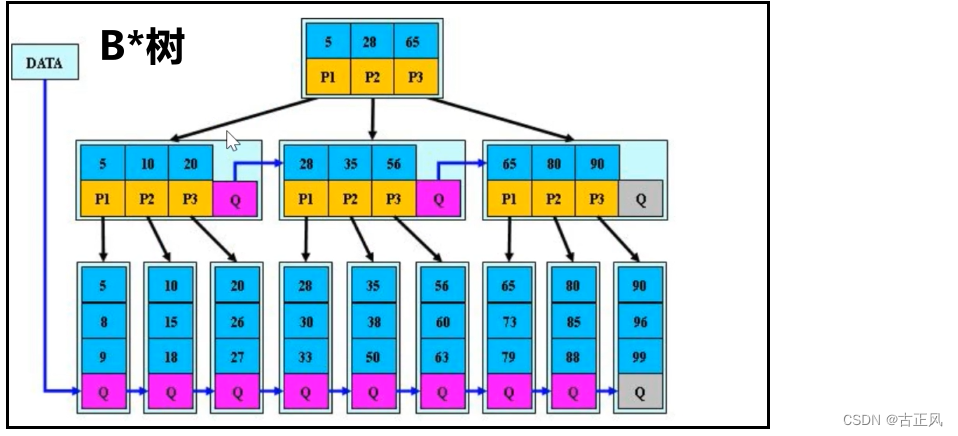
B*树是B+树的变体,B*树是在B+树的分支结点上再增加指向兄弟结点的指针
B*树定义了非叶子结点关键字个数至少为**(2/3)*M**,M是阶数,即块的最低使用率是2/3(B树和B+树是1/2)
B+树的分裂:当一个结点未满时,分配一个新的结点,并将原节点1/2的数据复制到新节点,最后在父结点中增加新节点的指针;B+树的分裂只影响原节点和父结点,而不会影响兄弟结点,所以他不需要指向兄弟的指针
**B*树的分裂:**当一个结点未满时,如果它的下一个兄弟结点未满,那么将一部分数据移到兄弟结点中,再在原节点插入关键字,最后修改父结点中兄弟结点的关键字(因为兄弟结点的关键字范围改变了);如果兄弟结点也满了,则在原节点与兄弟结点之间增加新 节点,并各复制1/3的数据到新节点,最后再父结点增加新节点的指针
所以:B*树分配新节点的概率要比B+树要低,空间使用率更高,在B+树的基础上,为非叶子结点也增加链表指针,将结点的利用率从1/2提高到2/3