题目

合并 k 个升序的链表并将结果作为一个升序的链表返回其头节点。

数据范围：节点总数满足 0≤n≤1050 \le n \le 10^50≤n≤105，链表个数满足 1≤k≤105 1 \le k \le
10^5 \ 1≤k≤105 ，每个链表的长度满足 1≤len≤200 1 \le len \le 200 \ 1≤len≤200
，每个节点的值满足 ∣val∣<=1000|val| <= 1000∣val∣<=1000 要求：时间复杂度
O(nlogk)O(nlogk)O(nlogk)

示例1

输入：
[{1,2,3},{4,5,6,7}]
返回值：
{1,2,3,4,5,6,7}

示例2

输入：
[{1,2},{1,4,5},{6}]
返回值：
{1,1,2,4,5,6}

解题思路

这道题看似很难，牛客网上定义的也是较难的题型，其实理解之后也没有特别难，只是使用了多次合并两个有序链表的方式。

我们会有一个链表的数组，要将所有的链表都合并成一个链表
第一想法就是，一个个去比，然后将小的数据不断地插入到链表中，但是这么实现的难度太大了，我们不知道数组当中到底有多少个链表，循环的次数难以确定。
那么如何将复杂的问题化简成简单的问题呢？
可以将链表的集合拆分正一对一对的链表对，我们每次只合并两个链表（这样操作起来就比较简单了）。
合并两个有序链表的代码如下：

ListNode* mergeTwoLists(ListNode* pHead1,ListNode* pHead2)
    {
    	//如果有一个链表为空，直接返回拎一个链表
        if(pHead1 == NULL) return pHead2;
        if(pHead2 == NULL) return pHead1;

		//添加一个头结点
        ListNode* res = new ListNode(0);
        ListNode* cur =res;
        
        //将链表的值一个一个的连到目标链表当中
        while(pHead1 && pHead2)
        {
            if(pHead1->val < pHead2->val)
            {
                cur->next = pHead1;
                pHead1 =pHead1->next;
            }
            else
            {
                cur->next = pHead2;
                pHead2 = pHead2->next;
            }
            cur = cur->next;
        }

		//将剩余的链表链到目标链表当中
        if(pHead1 != NULL) cur->next = pHead1;
        if(pHead2 != NULL) cur->next = pHead2;
        
        //返回合并的链表
        return res->next;
    }

那么新的问题有来了，我们如何将时间复杂度降到O(nlongK)呢？

这个时候让我想起了简单快速排序，快排的时间复杂度不就是O(nlogN)嘛。
那能不能仿照快排的方式，将链表的集合进行划分，然后递归的去归并呢？事实是可以的，我们从中间开始划分，不断地递归，知道我们的链表数只剩下两个或者一个的时候，进行合并，然后再不断地拼接，最终得到我们想要的链表

流程图：
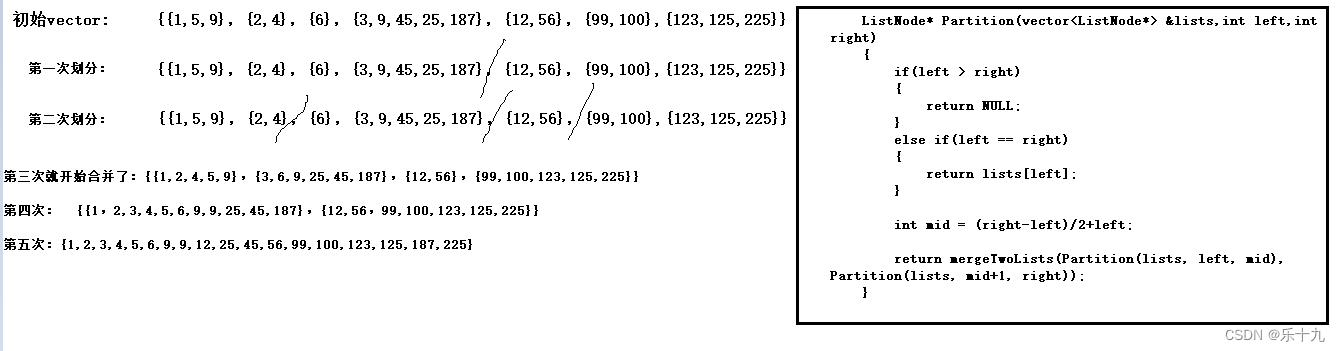
在这里插入图片描述

看实现：

//划分合并区间
    ListNode* Partition(vector<ListNode*> &lists,int left,int right)
    {
        if(left > right)
        {
            return NULL;
        }
        else if(left == right)
        {
            return lists[left];
        }
        
        int mid = (right-left)/2+left;
        
        return mergeTwoLists(Partition(lists, left, mid), Partition(lists, mid+1, right));
    }

整体代码：

class Solution {
public:
    //合并两个链表
    ListNode* mergeTwoLists(ListNode* pHead1,ListNode* pHead2)
    {
        if(pHead1 == NULL) return pHead2;
        if(pHead2 == NULL) return pHead1;
        ListNode* res = new ListNode(0);
        ListNode* cur =res;
        
        while(pHead1 && pHead2)
        {
            if(pHead1->val < pHead2->val)
            {
                cur->next = pHead1;
                pHead1 =pHead1->next;
            }
            else
            {
                cur->next = pHead2;
                pHead2 = pHead2->next;
            }
            cur = cur->next;
        }
        if(pHead1 != NULL) cur->next = pHead1;
        if(pHead2 != NULL) cur->next = pHead2;
        
        return res->next;
    }
    
    //划分合并区间
    ListNode* Partition(vector<ListNode*> &lists,int left,int right)
    {
        if(left > right)
        {
            return NULL;
        }
        else if(left == right)
        {
            return lists[left];
        }
        
        int mid = (right-left)/2+left;
        
        return mergeTwoLists(Partition(lists, left, mid), Partition(lists, mid+1, right));
    }
    
    ListNode *mergeKLists(vector<ListNode *> &lists) {
        return Partition(lists, 0, lists.size()-1);
    }
};