洛谷P1282 多米诺骨牌题解

题目链接：P1282 多米诺骨牌

题意：

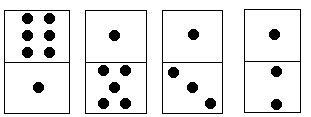
多米诺骨牌由上下 $2$ 个方块组成，每个方块中有 $1\sim6$ 个点。现有排成行的上方块中点数之和记为 $S_1$ ，下方块中点数之和记为 $S_2$ ，它们的差为 $\left|S_1-S_2\right|$ 。如图， $S_1=6+1+1+1=9$ ， $S_2=1+5+3+2=11$ ， $\left|S_1-S_2\right|=2$ 。每个多米诺骨牌可以旋转 $180 °$ ，使得上下两个方块互换位置。请你计算最少旋转多少次才能使多米诺骨牌上下 $2$ 行点数之差达到最小。

对于图中的例子，只要将最后一个多米诺骨牌旋转 $180 °$ ，即可使上下 $2$ 行点数之差为 $0$ 。

注意到我们其实并不关心 $S_1,S_2$ 的值，而是关心他们的差值

这个绝对值似乎不好处理，其实只要把正负的情况取个min就可以了

设 $d p [i] [j]$ 表示只考虑前 $i$ 个骨牌，差值为 $j$ 时的最小翻转数

这里的 $j$ 定义为 $S_1-S_2$ 或者 $S_2-S_1$ 其实没啥区别，不过下面代码为前者

不难发现

$dp[i][j]=\min(dp[i-1][j-a[i]+b[i]]+1,dp[i-1][j+a[i]-b[i]])$

注意到差值最大 $5000$ ，为了避免乱七八糟讨论，就直接循环 $\sim 5000$ 就好啦

差值可能为负所以数组整体平移一下，然后整个填表法滚一滚啥的就好了

~~这里好像刷表法写起来不太安全就不写了，虽然没啥问题，但是不算简洁吧（逃~~

代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define INF 0x3f3f3f3f3f3f3f3f
#define N (int)(1e3+15)
const int bd=5e3+15;
int n,dp[2][20*N],a[N],b[N];
signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);cout.tie(0);
    // freopen("check.in","r",stdin);
    // freopen("check.out","w",stdout);
    memset(dp,0x3f,sizeof(dp));
    cin >> n;dp[0][bd]=0;
    for(int i=1; i<=n; i++)
        cin >> a[i] >> b[i];
    for(int i=1; i<=n; i++)
    {
        int cur=i&1,pre=cur^1;
        memset(dp[cur],0x3f,sizeof(dp[cur]));
        for(int j=-5000; j<=5000; j++)
            dp[cur][j+bd]=min(dp[pre][j+a[i]-b[i]+bd]+1,dp[pre][j-a[i]+b[i]+bd]);
    }
    for(int i=0; i<=5000; i++)
    {
        int t=min(dp[n&1][i+bd],dp[n&1][-i+bd]);
        if(t<=n)return cout << t << endl,0;
    }
    return 0;
}